Закон Гаюі

Вчення про символи базується на одному з найважливіших законів кристалографії – законі раціональності відношення параметрів (законі Гаюі).

Припустимо що, ретельно вивчивши наші рекомендації з установки кристалів, Ви правильно розташували модель кристала в координатній системі, прийнявши за координатні осі три непаралельних ребра. А тепер поспостерігайте, де перетинаються координатні осі дві грані вашого кристалу при їх уявному продовженні (рис. 3.3). Одна – одинична (A₁B₁C₁), що вибрана у відповідності до сингонії за правилами табл. 3.1, відсікає відрізки ОА₁ ОВ₁ ОС_1, які називаються одиничними параметрами. Друга непаралельна грань (A_xB_xC_x) характеризується параметрами ОА_x,ОВ_x,ОС_x.

Закон Гаюі стверджує: подвійні відношення параметрів, що відтинаються двома будь-якими гранями кристала на трьох його ребрах, що перетинаються, дорівнюють відношенням цілих і порівняно малих чисел = 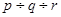(параметри Вейса)

Рис 3.3. Параметри та кристалографічні осі

Наявність цілих чисел пояснюється решітчастою будовою кристалів. Ребра кристалів відповідають рядам решітки, грані – плоским сіткам. Плоскі сітки (грані), перетинаючи три ряди решітки (ребра), утворюють на них відрізки (параметри), яки вміщують цілі числа проміжків між вузлами решітки (елементарними частками), рис. 3.3.

Наявність малих чисел пов'язана з тим, що реальні грані кристалів побудовані не будь-якими плоскими сітками, а тільки тими, які мають найбільшу щільність розташування у них елементарних часток.

Закон Гаюі зв'язує зовнішню форму кристалів з їх внутрішньою решітчастою будовою.

При практичному застосуванні закону Гаюі для визначення індексів граней користуються зворотними відношеннями параметрів, які отримали назву індексів Міллера:

= .

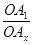
Індекси Міллера – це величини, зворотні до параметрів Вейса, наведені до цілих чисел.

Для одержання індексів Міллера у вигляді трьох взаємно простих чисел виконують такі математичні перетворення: приведення дробів до загального знаменника, відкидання загального знаменника, скорочення відношень на загальний множник. Як приклад, визначимо індекси Міллера для грані А_x В_x С_x (рис. 3.3). Параметри виразимо числом проміжків між елементарними частками (в мм чи см):

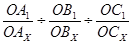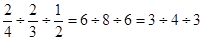= ; індекс грані А_xВ_xС_x – (343).

Таким чином, будь-яку грань А_xВ_xС_x, а точніше, її нахил до кристалографічних осей можна охарактеризувати трьома цілими і взаємно простими числами – індексами (hkl), що представляють відношення трьох дробів, чисельники яких є параметри одиничної грані (ОА₁, ОВ₁ ,ОС₁), а знаменники відповідають параметрам грані (OA_x ,OB_{x ,}OC_x), що визначається.

Після математичних перетворень індекси мають вигляд невеликих цілих чисел. Але слід пам'ятати, що чим більший параметр грані, тобто чим більший відрізок відтинає грань на координатній осі, тим менший індекс вона має на даній осі. Умовні позначення символів:

– грань (hkl) або (hkil) – для кристалів тригональної та гексагональної сингоній; h – індекс по осі X; k – індекс по осі Y;

i- індекс по осі U, l – по осі Z; плоска сітка кристалічної решітки;

– ребро [hkl], ряд кристалічної решітки;

– вершина [[hkl]], вузол кристалічної решітки;

– проста форма – {hkl}.

Якщо грань перетинає якусь вісь з негативного боку, то над індексом по цій осі становлять знак мінус (hk .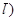

Як символ простої форми вибирається грань, що має максимальну кількість позитивних індексів.

На практичних заняттях з кристалографії відрізки, що відтинаються гранями на координатних осях, визначаємо наближено за допомогою лінійки та олівця. Більш точні розрахунки виконуються на основі спеціальних формул з застосуванням гоніометричних вимірів.