Обнаружение радиолокационных сигналов 7 страница

Разрешающая способность РЛС по дальности численно характеризуется минимальным расстоянием между двумя целями, имеющими одинаковые угло­вые координаты (расположенными в радиальном относительно РЛС направле­нии), при котором еще возможно раздельное наблюдение этих целей.

На рис. 1.6.1,апоказаны две точечные цели с одинаковыми угловыми ко­ординатами. Отметки целей для идеализированного случая сигналов прямо­угольной формы и неискажающего приемно-индикаторного тракта изображены на рис. 1.6.1,6. При сближении целей две отметки принимают вид двугорбой кривой, которая при интервале между целями Δt₃ ≤ τ_и становится одногорбой. Примем в качестве условия разрешения двух целей наличие впадины между ними, т. е. когда отметка еще является двугорбой. Так как Δt₃ = t_з2 – t_з2 = 2(D₂ –D₁)/ с, то условие разрешения состоит в том, чтобы (D₂ –D₁) > сτ_и/2. Отсюда разрешающая способность по дальности, которую в данном случае можно ус­ловно назвать идеальной (так как не учитывается влияние приемника и инди-

катора), равна δD_ид = τ_и/2.

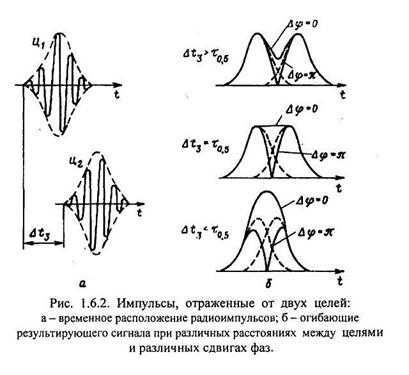
На рис. 1.6.2. показан случай, когда форма сиг­налов, отраженных от двух близко расположен­ных целей, отличается от прямоугольной. Высоко­частотные колебания этих сигналов накладываются одно на другое. Всегда возможно случайное из-

менение расстояния между целями по крайней мере от 0 до λ/4 (например, при λ =10 см для этого потребуется, чтобы расстояние изменилось всего лишь на 2,5 см). Это соответствует случайному изменению разности фаз от Δφ = 0 до Δφ = π, т. е. фактически импульсы, отраженные от двух целей, при соответст­вующем времени наблюдения, являются некогерентными.

На рис. 1.6.2,6изображены огибающие результирующего сигнала для двух крайних случаев сдвига фаз Δφ = 0 и Δφ = π при трех значениях временного интервала между целями Δt₃. При Δt₃ > τ_0.5, где τ_0..5 — длительность импульса на уровне 0,5 от максимальной амплитуды, огибающая суммарного сигнала при любой разности фаз является двугорбой. При Δt₃ < τ_0.5 огибающая в зави­симости от разности фаз может быть двугорбой или одногорбой, как для оди­ночной цели. Наконец, пересечение на уровне 0,5 от максимальной амплитуды, когда At₃ = т_о,5, соответствует граничному случаю, так как при Δφ = 0 двугорбая кривая только начинает исчезать. Дальнейшее сближение целей приводит к все увеличивающейся вероятности ошибочного решения о количестве целей. От­сюда в соответствии с критерием разрешения Релея можно принять

δD_ид = сτ_0,5/2 (1.6.2)

Условность такого определения разрешающей способности вытекает, на­пример, из того, что по характеру флуктуации отметки цели на экране индика­тора (особенно с линейной разверткой) оператор даже при Δt₃ < τ_0,5, может сде­лать вывод о наличии групповой цели, т. е. фактическая разрешающая способ­ность будет выше чем сτ_0,5/2.

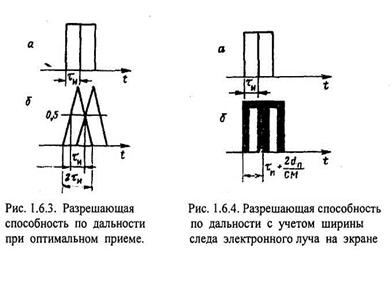
Идеальная разрешающая способность [формулы (1.6.1) и (1.6.2)] является фактически потенциальной δD_пот, т. е. предельно достижимой. Это можно пояс­нить путем анализа разрешающей способности в случае оптимальной обработ­ки сигнала (с помощью согласованного фильтра). Если зондирующие импульсы имеют прямоугольную форму с длительностью τ_и, то на выходе оптимального приемника (согласованного фильтра) образуются треугольные импульсы с дли­тельностью основания 2τ_и (см. п. 4.3.1). Как видно из рис. 1.6.3, если огибаю­щие импульсов на входе приемника соприкасаются (рис. 1.6.3,а), то на выходе

они пересекаются на уровне 0,5 (рис. 1.6.3,6) и разрешающая способность фак­тически определяется формулой (1.6.1), т. е. оптимальный приемник не ухуд­шает разрешающей способности. Поэтому в общем случае

(при непрямоугольной форме импульсов принимают τ_и = т_0,5).

Таким образом, по­вышение разрешающей способности по дальности связано с необходимо­стью сокращения дли­тельности импульсов. Это можно расценивать как расширение спектра сиг­нала. Так, для прямо­угольного радиоимпульса

длительностью τ_и ширина спектра по нулям главного лепестка диаграммы на­правленности Δf_c = 2/τ_и, откуда после подстановки в (1.6.3) получим

Эта закономерность, как будет видно из дальнейшего, имеет общий харак­тер: для повышения разрешающей способности по дальности всегда требуется расширение спектра сигнала.

Реальная разрешающая способность по дальности может оказаться гораздо хуже потенциальной. В РЛС с визуальным индикатором существенное влияние оказывает ширина следа электронного луча на экране ЭЛТ. На рис. 1.6.4 пока­зано два импульса на границе их разделения без учета (рис. 1.6.4,а) и с учетом (рис. 1.6.4,6) толщины следа. Толщина следа определяется диаметром сфоку­сированного пятна на экране ЭЛТ d_n. Согласно (1.1.4) этому соответствует

дальность d_n/M, или временной интервал 2d_п/cM. В данном случае разрешаю­щая способность по дальности, как видно из рис. 1.6.5,6, равна

где δD_пот — потенциальная разрешающая способность, определяемая по формуле (1.6.3), a δD_э - разрешающая способность экрана.

Разрешающая способность экрана на основании формул (1.1.4) и (1.3.1) равна

где к_э = 1_шк/d_э — коэффициент использования диаметра экрана (для инди­катора с линейной разверткой (типа А) к_э ≈0,8, для ИКО к_э< 0,5).

2.3.3. Разрешающая способность по углу

Разрешающая способность по угловой координате (направлению) числен­но характеризуется минимальным углом (по азимуту или углу места) между направлениями на две равноудаленные относительно РЛС цели, при котором еще возможно их раздельное наблюдение.

Понятие разрешающей способности вы­ясним на примере РЛС кругового обзора. Две равноудаленные цели с близкими азимута­ми при вращении антенны (рис. 1.6.6,а) создают на входе приемника, как и следует из п. 1.6.1, две перекрывающиеся пачки импуль­сов (рис. 1.6.6,6). Совпадающие импульсы этих пачек образуются вследствие облучения целей одним и тем же зондирующим импуль­сом.

Предположим, как и в предыдущем слу­чае, что происходит случайное изменение

расстояния до целей не меньше, чем на λ/4, т. е. рассматриваемые пачки им­пульсов некогерентны. Тогда задача разделения сводится к уже рассмот­ренной для двух сигналов со случайными фазами, пересекающихся на опре­деленном уровне. Отличие лишь в том, что сигналы имеют вид не одиноч­ных импульсов, а пачки импульсов. Здесь сохраняется в силе анализ, про­веденный на рис. 1.6.2 применительно к огибающим пачек. Разделение це­лей можно считать еще возможным, когда огибающие пересекаются на уров­не 0,5 от максимальной амплитуды.

Так как огибающая пачки согласно формуле (1.4.4) соответствует диа­грамме направленности по мощности, то пересечение пачек на уровне 0,5 озна­чает угловой сдвиг целей на ширину диаграммы направленности по точкам по­ловинной мощности θ_0.5. Таким образом, потенциальная разрешающая способ­ность по азимуту

Для повышения потенциальной разрешающей способности по углу требу­ется, таким образом, сужение диаграммы направленности антенны, что при за­данных размерах антенны связано с укорочением длины волны.

Разрешающая способность заметно ухудшается за счет влияния ЭЛТ и

равна

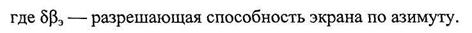
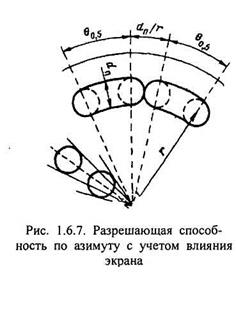
Из рис. 1.6.7 следует, что за счет конечного

диаметра пятна d_п размеры отметки цели возрас­тают на величину d_п. Поэтому к ранее найденной величине потенциальной разрешающей способно­сти (1.6.8) добавляется угловая ширина диаметра пятна

δβ_э = d_п/r, (1.6.10)

где г — радиус соответствующей отметки на экране.

Для ИКО характерна зависимость разрешающей способности экрана от положения отметки цели относительно центра экрана. По мере приближения отметки к центру экрана разрешающая способность по углу ухудшается. Это иллюстрируется изменением углового размера пятна на рис. 1.6.7.

Указанный недостаток ИКО устраняется при переходе к индикатору, ази­мут и дальности (ИАД) с прямоугольным растром, в котором длина отметки цели в азимутальном направлении постоянна (см. рис. 1.3.8,а).

При этом разрешающая способность экрана

где М_β = 1_шказ/β_шк — азимутальный масштаб (1_шказ — длина шкалы азимута; β_шк — просматриваемый азимут).

Для повышения разрешающей способности экрана по азимуту следует использовать более крупный масштаб и ЭЛТ с высоким качеством фокуси­ровки Q_ф.

Важным параметром в ряде случаев является линейная разрешающая спо­собность в тангенциальном направлении, т. е. минимальное расстояние между двумя целями в тангенциальном направлении при одинаковом расстоянии в ра­диальном направлении (например, отрезок Ц₁Ц₂ на рис. 1.6.6,а), при котором их можно разделить. Она равна

т. е. растет линейно с повышением дальности.

2.3.4. Разрешаемый объем

Разрешаемый объем РЛС, именуемый также (при импульсном методе) импульсным объемом, является обобщенной мерой разрешающей способности.

Он характеризует часть пространства, облучаемого РЛС, в пределах которого цели не наблюдаются раздельно.

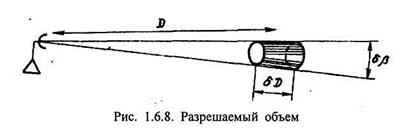
Разрешаемый объем ограничивается диаграммой направленности антенны. Его проще всего определить при использовании иглообразного (конического) луча (рис. 1.6.8). На достаточно большом расстоянии от РЛС часть конуса близка к цилиндру, у которого сторона

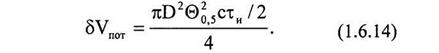
равна βD а диаметр основания Dβδ. Поэтому разрешаемый объем

В случае целей, равномерно рассеянных в объеме (например, гидрометео­ры), интенсивность отраженного сигнала определяется разрешаемым объемом. Уменьшение последнего позволяет снизить мешающее действие таких объек­тов.

Понятие разрешаемого объема позволяет уточнить определение точечной цели (см. п. 1.4.1): ее размеры должны быть заметно меньше элементов разре­шаемого объема. В этом случае ни длительность всей пачки, ни длительность ее отдельных импульсов при отражении заметно не изменяются.

2.4. Распознавание воздушных объектов

Одно из важнейших направлений современной радиолокации - создание методов получения наиболее полной информации, содержащейся в радиолока­ционных сигналах и помехах. Радиолокационное распознавание является ча­стью данного направления. Распознавание осуществляется за счет взаимных различий сигналов от воздушных объектов.

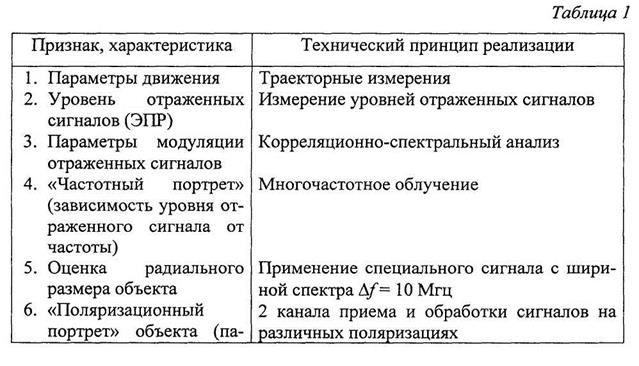
Для распознавания могут быть использованы временные, спектральные, корреляционные, энергетические, пространственные, поляризационные харак­теристики отраженных сигналов с применением устройств внутри - межпери-одной, межобзорной и межканальной обработки, траекторного анализа. Целе­сообразен анализ излучения бортовых средств. Информативность отдельных признаков распознавания неодинакова, но, очевидно, увеличение числа призна­ков в целом уменьшает вероятность ошибочных решений.

Реализация методов распознавания определяется видом применяемых зондирующих сигналов и способами обработки. Все методы можно разделить на две группы. Одна группа базируется на использовании информации, содер­жащейся в структуре отраженных сигналов (сигнальные признаки). Для распо­знавания используются такие важные характеристики воздушных объектов, как их размеры и форма, особенности движения отдельных частей объекта (враще­ние винтов, турбин, вибрация элементов корпуса и другие) и всего объекта в целом.

Другая часть методов использует траекторные признаки.

Наилучшие качественные показатели достигаются при использовании широкополосных зондирующих сигналов, обеспечивающих получение радио­локационных портретов воздушных объектов.

В случае, если отдельные элементы объекта не разрешаются, использу­ются энергетические, флюктуационные характеристики, спектр спектр допле-ровских частот, поляризационные свойства отраженного сигнала. Известно, что воздушные объекты создают отраженные сигналы, параметры которых флюк­туируют в широких пределах. Степень флюктуации зависит от характера объ-

екта отражения и тем выше, чем сложнее объект и больше его размеры. Оценка флюктуации является одним из признаков распознавания.

Наличие информации об уровнях отраженных сигналов позволяет прово­дить оценку эффективных поверхностей рассеяния (ЭПР), которые являются еще одним из признаков распознавания.

Анализ флюктуации огибающих пачек отраженных сигналов способству­ет выявлению модуляционных характеристик, зависящих от особенностей воз­душных объектов.

При наличии двух и более частотных каналов в составе средства радио­локации предпочтителен взаимно-корреляционный признак. Сигналы, отра­женные от объектов с общим числом «блестящих» точек на различных частотах будут не коррелированы (слобокоррелированы), в то время, как сигналы от объектов с малым числом «блестящих» точек статистически зависимы.

При отражении радиоволн от распознаваемых объектов поляризации па­дающих и отраженных волн различаются. Поляризация отраженного сигнала изменяется в общем случае из-за различия амплитуд и фаз сигналов, отражае­мых отдельными элементами конструкции. Анализ поляризационной матрицы рассеяния позволяет проводить распознавание воздушных объектов.

В таблице 1 представлены возможные признаки для распознавания.

Использование отдельных признаков требует внедрения технических уст­ройств анализа различной степени сложности, применения сигналов специаль­ной формы.

2.4.1. Постановка задачи. Качественные характеристики распознавания

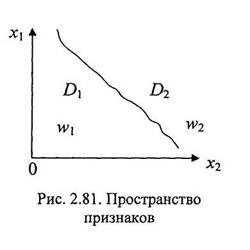
Заданы классы объектов w1, ... wm, характеризуемые признаками xl, ..., xn. Если объект, имеющий признаки х₁°, ..., x_n° относится к классу wi, то в про­странстве признаков характеризующая его точка расположена в области Di. На же. 2.81 изображено разбиение двумерного пространства на области D1 и D2, соответствующие классам w1 и w2. Необходимо определить алгоритмы, обес-течивающие отнесение воздушного объекта к тому или другому классу. Про-

блему оптимизации процедуры распознавания объектов можно разрешить на основе стати­стической теории многоальтернативного (в ча­стном случае двухальтернативного ) распозна­вания. Для классической процедуры анализа система должна определять отношение прав­доподобия или его логарифм и сравнивать его с порогом. Обозначим

X = {х₁, х₂,..., х_п} - вектор входного сигнала; W(x/w_l), w(x/w₂) - условные плотности вероятности отраженных сигналов; w1, w2 — признаки, характеризующие принадлежность объекта к различным классам.

Отношение правдоподобия определяется как

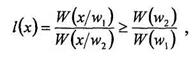
где W(w1), W(w2) - априорные вероятности признаков w\ и w2, W{w2)/W(w1) - пороговое значение отношения правдоподобия.

Решение задачи распознавания заключается в выявлении двух гипотез: Н1 - объект относится к классу, который характеризуется признаками w1;H2-объект с признаками w2. Если отношение правдоподобия превышает пороговое значение, принимается гипотеза H1, если нет - гипотеза Н2. В случае использо­вания вместо отношения правдоподобия его логарифма, решающее правило имеет вил

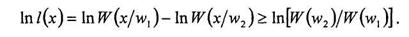
Приведенные уравнения являются оаиесовским критерием, минимизи­рующим ошибки решения задачи распознавания.

Вероятность ошибки является ключевым параметром в статистической теории распознавания. Различают два типа ошибок: ошибки первого рода, ко­гда объект, характеризуемый признаками w\ отнесен к объекту с признаками w2; ошибки второго рода, когда объект с признаками w2 отнесен к объекту с признаками w\. Общая ошибка определяется как взвешенная сумма названных ошибок

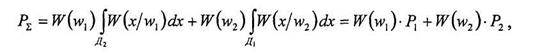
где Д1 и Д2 - пространства признаков w1 и w2;

P1 и Р2 - ошибки первого и второго рода соответственно.

Часто ошибки Р1 и Р2 определяют путем интегрирования плотности ве­роятности отношения правдоподобия W(l/w_i)

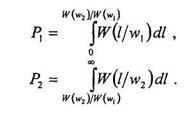
Вычисление вероятности ошибочных решений сводится по существу к интегрированию в п мерном пространстве плотности вероятности анализируе­мых сигналов. Получить значение вероятности ошибки в явном виде зачастую не удается из-за сложности математических вычислений с одной стороны и не­возможности точного определения плотности вероятности анализируемых сиг­налов с другой стороны. При решении многих практических задач применяют­ся или экспериментальные методы или критерии, связанные не с самой вероят­ностью ошибок, а с ее границами.

Вероятность ошибки распознавания может быть определена следующим образом

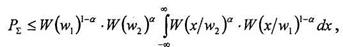
где α — действительное число, изменяющееся от 0 до 1.

Приведенное неравенство носит название границы Чернова для верхнего зна­чения вероятности ошибки.

Нахождение оптимального значения α связано с рядом трудностей. Вследствие этого, а также учитывая, что α в окрестности оптимального значе­ния обладает малой чувствительностью, положим α=0,5.

Среднюю вероятность ошибки можно определить следующим образом

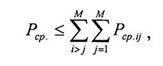
где М- число сигналов для распознавания;

P_cp.ij - средняя вероятность ошибки распознавания i-го j-го сигналов. При использовании границы Чернова

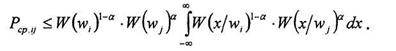
При известных учитывая что

(α=0,5) средняя вероятность ошибки определится как

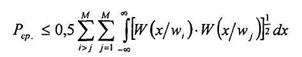
Для случая двухальтернативной классификации

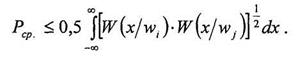
Следует заметить, что если взять логарифм натуральный со знаком минус от интеграла, получим известное расстояние Бхаттачария (В) или функцию раз­личимости, которая является критерием разделимости классов.

Учитывая приведенное выра­жение можно записать:

Р_ср=0,5-е^-B; D = 1-P_cp=1-0,5·e^-B где D - вероятность правильного

решения задачи.

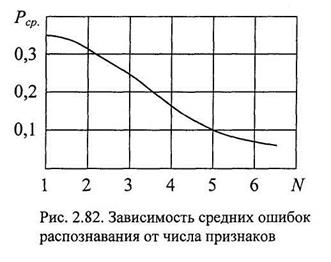
Использование нескольких призна­ков для распознавания позволяет уменьшить среднюю вероятность ошибочных решений. Если признаки

характеризуются одинаковыми распределениями вероятностей, зависимость средних ошибок распознавания от числа признаков N имеет вид, изображенный на рис. 2.82. Увеличение числа признаков с одного до четырех в два раза уменьшает ошибки распознавания.

Возможно несколько подходов к классификации методов распознавания:

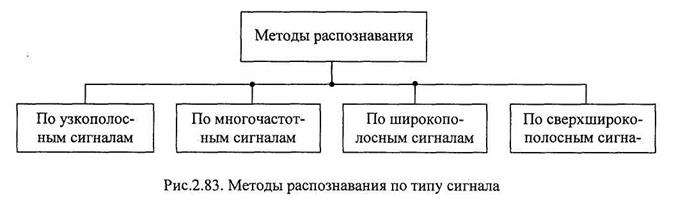
по типу зондирующего сигнала, виду используемой радиолокационной инфор­мации и др. Наиболее широко используется распознавание по типу зондирую­щего сигнала. На рис. 2.83 изображен вариант такого распознавания.

2.4.2. Распознавание по широкополосным сигналам

Широкополосные зондирую­щие сигналы обеспечивают достиже­ние наилучших качественных показа­телей распознавания. В этом случае удается разрешить отдельные эле­менты воздушного объекта и полу­чить его радиолокационный портрет.

На рис. 2.84 изображен радиолокации-

онный портрет воздушного судна типа Як-40. Для получения радиолокацион-ного портрета формируется зондирующий сигнал (например с линейной час-тотной модуляцией) с девиацией частоты 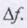Отраженные от объекта радиоим­пульсы сжимаются согласованным фильтром, при этом их длительность на вы­ходе фильтра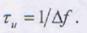

Распознавание и идентификация объектов в РЛС может осуществляться сравнением радиолокационного портрета с эталонными портретами.

Применение когерентных широкополосных сигналов с шириной спектра 50-100 МГц позволяет обеспечить разрешающую способность в 2-3 метра. При таком разрешении и сформируется радиолокационный портрет объекта. Досто­инством таких сигналов является возможность распознавать несколько объек­тов в пределах одного импульсного объема. Применение широкополосных сиг­налов имеет ряд особенностей. Во-первых, резко возрастает число элементов разрешения, что ведет к увеличению объема аппаратуры обработки. Во-вторых, дробление пачки отраженного сигнала на отдельные составляющие ухудшает отношение сигнал/шум, что обусловливает уменьшение дальности обнаруже­ния. Отношение дальности распознавания к дальности обнаружения за один обзор составляет 0,7 для объектов больших размеров и 0,95 для малоразмерных объектов. При нескольких обращениях к объекту это отношение улучшается. Применение метода широкополосных сигналов в нескольких пунктах дает воз­можность определить форму распознаваемых воздушных объектов.

2.4.3. Распознавание по многочастотным сигналам

Многочастотный сигнал позволяет получить некоторый функционал ра­диолокационного портрета объекта. Применение сигнала для распознавания возможно в диапазоне метровых и сантиметровых волн. Наиболее информатив­ными признаками распознавания являются: радиальный размер объекта, сред­нее значение модуля поляризационного коэффициента, среднее значение эф­фективной поверхности рассеяния. По совокупности этих признаков многочас­тотный сигнал позволяет получить достаточно высокие характеристики распо­знавания.

Формирование многочастотных сигналов может быть реализовано раз­личными путями. При одновременном излучении зондирующих сигналов на различных частотах получение информации для распознавания требует много-канальности построения приемо-передающих устройств, что ведет к увеличе­нию объема аппаратуры и энергозатратам. Может быть отдано предпочтение сигналам с последовательным излучением сигналов на различных частотах, не требующим существенного усложнения аппаратуры, однако, увеличивающего время анализа и принятия решения.

При облучении воздушных объектов сигналами с достаточно широким спектром эти объекты эквивалентны некоторым линейным электрическим фильтрам с постоянными параметрами, резонансные частоты которых опреде­ляются формой объекта и ее геометрическими размерами. Резонансные частоты проявляются в переходном процессе отклика, т.е. в отраженном сигнале. Сиг­нал с широким спектром может быть получен при использовании коротких им­пульсов либо многочастотных сигналов. Переходные процессы могут быть описаны либо дифференциальными уравнениями, либо преобразованиями Лапласа. В последнем случае от операций с оригиналами переходят к операциям с изображениями.

Изображение G(p) , характеризующее передаточную функцию линейной системы, может быть представлено в виде

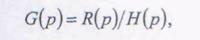
где R(p) - изображение по Лапласу отклика;

Н(р) - изображение по Лапласу некоторого импульсного воздействия

на систему.

Изображения R(p) и (р) являются полиномами от P_i = а + jb, bи а - мнимая

и вещественная части корня полинома Pi. Корни полинома Н(р) называют по­люсами.

Отклик системы h(p) в физическом смысле - это либо распределение то­ков на поверхности распознаваемого объекта, либо напряженность поля рассе­янной части волны Е. Форма отклика может быть представлена в виде набора дискретных отсчетов

где Ai- набор вычетов изображения Лапласа;

т = 0, 1, ..., М;

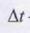- шаг дискретизации во времени;

N- общее число дискретных отсчетов.

Процесс распознавания можно представить следующим образом. Сигна­лы, отраженные от объектов, анализируются, в результате чего вычисляются полюса. Полученные значения полюсов сравниваются с эталонами, записанны­ми в блоке памяти.

Метод, использующий зависимость интенсивности отраженных сигналов от длины волны зондирующего сигнала базируется на фундаментальном физи­ческом эффекте вторичного излучения объектов. Интенсивность отражения от каждого токопроводящего объекта зависит от его формы и размеров, а также от длины волны. На низких частотах большинство объектов не отражают падающие электромагнитные волны. При повышении частоты до значения, при кото­ром размеры отражающего объекта приближаются к λ/2 РЛС, интенсивность отражений, характеризующая эффективную поверхность рассеяния объекта, резко увеличивается. Если размер объекта равен λ /2, то эффективная поверх­ность рассеяния максимальна. При дальнейшем возрастании частоты эффек­тивная поверхность рассеяния будет изменяться и носить колебательный харак­тер. При длине волны значительно меньшей линейных размеров объекта, эф­фективная поверхность практически неизменна. Таким образом, анализ интен­сивности отраженных сигналов на различных частотах является существенным признаком распознавания.

Величина эффективной поверхности рассеяния, полученная на основе многочастотного сигнала, может быть отмечена в виде точки на частотно-пространственной траектории. Местоположение точки будет зависеть от типа, размера облучающего объекта, угла облучения и вида поляризации. Сравнение траектории точки с эталоном позволяет произвести распознавание воздушных объектов.