Обнаружение радиолокационных сигналов 5 страница

,

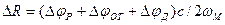где Δφ_р, Δφ_от, Δφ_д— абсолютные ошибки определения разности фаз, сдвига фа­зы при отражении и сдвига фазы в цепях дальномера соответственно. Дальномерная ошибка обратно пропорциональна масштабной частоте. Поэтому для уменьшения ΔR нужно увеличивать ω_м. Однако при этом будет уменьшаться диапазон однозначного измерения дальности. Дело в том, что однозначное из­мерение разности фаз двух колебаний возможно в пределах не более 2π. Следо­вательно, для однозначного измерения дальности необходимо, чтобы

,

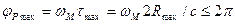т. е. частота f_м = ω_м/2π; масштабных колебаний и их период Т_м = l/f_м должны удовлетворять условию

, .

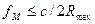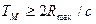Этому условию удовлетворяют сравнительно низкие частоты. Например, при R_max = 150 км f_м 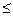1 кГц. Чтобы обеспечить требуемую точность и в то же время однозначность фазовой дальнометрии, используют две масштабные час­тоты или более, т. е. применяют многошкальный метод измерения дальности. Вначале однозначно измеряют дальность на низкой масштабной частоте, т. е. по грубой шкале. Затем измерения производят на второй, более высокой мас­штабной частоте, т. е. по более точной шкале. При этом, чтобы сохранялась однозначность дальнометрии, период второй масштабной частоты Т_2м должен превышать погрешность измерения временного запаздывания Δτ₁ на первой масштабной частоте (т. е. по грубой шкале).

Достоинства фазовой дальнометрии: малая пиковая мощность генерируе­мых колебаний благодаря непрерывности излучения, возможность изменения малых дальностей, простота измерителя, сравнительно малая аппаратурная по­грешность. Недостатки: отсутствие разрешения объектов по дальности, необхо­димость использования двух антенн для эффективной развязки передающего и приемного каналов.

Фазовый разностно-дальномерный метод.Определение разности рас­стояний фазовым методом сводится к измерению разности фаз двух когерент­ных колебаний, поступающих в точку приема из двух разнесенных РНТ. Пусть в РНТ А и В (рис. 2.50) расположены радиостанции, излучающие сигна­лы S_A = α_Acos (ω_At + φ_A0), S_B = α_Bcos (ω_Bt + φ_B0). Для простоты изложения сути метода предположим, что ω_A = ω_B=ω, φ_A = φ_B = φ₀. Тогда в точке М текущие значения фаз колебаний, прошедших расстояния R_A и R_B:

.

Если РПрУ в точке М принимает рассматриваемые два сигнала раздельно и подает их на фазометр, то последний измерит разность фаз

.

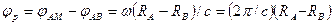Отсюда разность расстояний

.

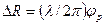Множеству постоянных значений разностей расстояний {ΔR_i =const, i= 1, 2,...} соответствует семейство линий положения в виде софокусных гипербол (рис. 2.50). Местоположение подвижного объекта определяется точкой пересе­чения двух гипербол (т. е. нужны две пары радиостанций).

Среднеквадратическая ошибка определения разности расстояний

,

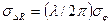где σ_φ— среднеквадратическая погрешность измерения разности фаз. Как ви­дим, для повышения точности измерения разности расстояний необходимо уменьшать длину волны (повышать частоту). Однако при этом может возник­нуть многозначность отсчета ΔR.

Однозначное измерение разности фаз будет при 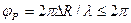. Следо­вательно, максимальное значение разности расстояний, измеряемой однознач­но, ΔR_max ⁼ λ. При ΔR > ΔR_max показания фазометра повторяются, что и влечет многозначность отсчета разности расстояний. Линии положения, для которых разность фаз между сигналами из двух РНТ кратна 2π, разделяют рабочую зону РНС на области однозначного отсчета — фазовые дорожки (см. рис. 2.50). Ширина дорожки d₀, т. е. кратчайшее расстояние ММ^’ между двумя линиями положения:

,

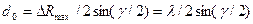где γ — угол, под которым видна база d из точки М. Если эта точка лежит на базе, то γ =180° ^и ширина дорожки минимальна: d_omin= λ/2. Следовательно, чис­ло дорожек

.

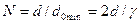Приведенные соотношения используют при расчете масштабной сетки линий положения, которые наносят на специальную навигационную карту. Не­однозначность отсчета можно устранить с помощью счетчика фазовых циклов, срабатывающего каждый раз, когда разность фаз принимаемых сигналов пре­вышает 2πn, n = 1,2,.... Неоднозначность измерений устраняют также примене­нием многошкального метода: с помощью дополнительных сеток линий поло­жения, образуемых при использовании более низких частот, на которых изме­ряется разность фаз.

Для реализации рассмотренного фазового разностно-дальномерного ме­тода необходимо обеспечить раздельный прием сигналов, приходящих из двух РНТ. Однако при работе радиостанций на одной несущей частоте это практиче­ски неосуществимо, так как излучаемые сигналы будут интерферировать в про­странстве и РПрУ примет суммарный сигнал, из которого нельзя извлечь информацию о разности расстояний. Для преодоления этой трудности использу­ют частотную либо временную селекцию сигналов. Частотную селекцию обес­печивают излучением сигналов на разных несущих частотах ω_А и ω_B причем

удобно, чтобы ω_А / ω_B = m/n, где m и n — целые числа. Такие сигналы прини­маются РПрУ по разным частотным каналам; после усиления сигналы с помощью умножителей частоты приводятся к одной частоте ω = ω_An = ω_Bm, на ко­торой изменяется разность фаз. Временную селекцию сигналов обеспечивают строгим разграничением излучения каждой радиостанции по времени.

Частотный метод.При этом методе дальнометрии излучается непрерыв­ное частотно-модулированное колебание; время запаздывания определяется пу­тем измерения частоты биений между излучаемым и принимаемым сигналами. Передатчик, состоящий из частотного модулятора ЧМ и генератора высокой частоты ГВЧ (рис. 2.51,а), генерирует колебания, частота которых меняется по периодическому закону — пилообразному или гармоническому. При симмет­ричном пилообразном законе модуляции (рис. 2.51,б) частота излучаемых ко­лебаний f₁(t) = f₀ + 2f_дt/T_M, 0 ≤ t ≤ Т_м/2, где f₀ — начальное значение частоты; f_д — девиация частоты; Т_м = 1/F_M — период модуляции. Частота принимаемого сигнала f₂(t) изменяется по такому же закону (при неподвижном объекте), при этом f₂(t) = f₀ + 2f_д(t - τ) / Т_м из-за задержки сигнала на время τ =2R/c. На выхо­де смесителя См образуется биения разностной частоты f_б = f₁(t) – f₂(t)=4 f_дF_MR/c, которые после усилителя низкой частоты УНЧ поступают на частот­ный анализатор ЧА. В результате R = сf_б/4f_дF_M.

Частотный анализатор может быть последовательным (одноканальным) либо параллельным (многоканальным). Последовательный анализатор — перестраи­ваемый по частоте узкополосный фильтр. При таком построении анализатора приходится тратить время на поиск сигнала по частоте, что приводит к энерге­тическим потерям. Этого недостатка нет в параллельном частотном анализато­ре, состоящем из набора узкополосных фильтров, перекрывающих диапазон возможных частот биений. В этом случае можно одновременно измерять даль­ность до многих целей. Недостатком параллельного спектроанализатора по сравнению с последовательным является увеличение объема аппаратуры.

Относительная погрешность измерения дальности

,

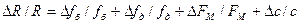где Δf_б/f_б — относительная погрешность измерения частоты биений; Δf_д/f_д, ΔF_M/F_M, Δc/c - относительные нестабильности девиации частоты, частоты мо­дуляции и скорости распространения волн соответственно.

В рассматриваемом дальномере появляется также дополнительная мето­дическая погрешность, обусловленная спецификой используемого метода. Из-за периодичности модуляции сигнала спектр биений близок к дискретному, причем спектральные линии расположены в точках f = kF_M, k = 1, 2,.... Частот­ный анализатор определяет частоту биений по положению спектральной линии с наибольшей амплитудой. При этом минимальное изменение частоты биений, которое можно зафиксировать, Δf₆=F_M. Следовательно, фиксируемое мини­мальное изменение дальности ΔR = cΔf₆/4f_дF_M = c/4f_д. Эта величина и дает мето­дическую погрешность частотной дальнометрии. Она же определяет наимень­шие измеряемое и разрешаемое расстояния. Для уменьшения ΔR необходимо увеличивать девиацию частоты f_д, т. е. расширять спектр зондирующего сигна­ла.

Основные достоинства частотной дальнометрии: малая пиковая мощ­ность зондирующего сигнала, возможность разрешения объектов по дальности. Недостатки: трудности обеспечения эффективной развязки передающего и приемного каналов, высокие требования к линейности изменения частоты.

2.2. 6. Методы измерения угловых координат

Измерение угловых координат основано на определении угла прихода радио­волн, излученных или отраженных объектом. Для этого используют радиопе­ленгаторы. Важной характеристикой радиопеленгатора является его пеленгационная характеристика и(α),— зависимость нормированного выходного на­пряжения приемника от направления прихода радиоволн. В зависимости от то­го, какой параметр радиосигнала оказывает основное влияние на формирование пеленгационной характеристики, методы углометрий (пеленгации) подразде­ляют на амплитудные, фазовые, частотные и комбинированные (амплитудно-фазовые). Основными из этих методов, нашедшими распространение на прак­тике, являются первые два; их мы и рассмотрим.

Амплитудные методы. Амплитудные методы пеленгации основаны на использовании направленных свойств антенн. Если используются направлен­ные свойства только приемной антенны, ДН которой равна f_пр(a), то пеленгационная характеристика радиопеленгатора u(α)=кf_пр(α), где к — коэффициент пропорциональности. При использовании направленных свойств как приемной, так и передающей антенны u(α)=к`f<sub>пр</sub>(α) f<sub>пер</sub>(α), где f<sub>пер</sub>(α) — ДН передаю­щей антенны. Если на передачу и прием работает одна антенна, то f<sub>пер</sub>(α) = f<sub>пр</sub>(α) = f(α), при этом u(α)=к`f²(α).

Среди амплитудных методов пеленгации различают методы максимума, минимума и сравнения. Пеленгация методом максимума (рис. 2.52,а) осущест­вляется путем совмещения направления максимума пеленгационной характери­стики α с направлением на пеленгуемый объект α₀ в результате плавного вра­щения ДН антенны; пеленг отсчитывается в тот момент, когда напряжение на выходе приемника становится максимальным. Достоинства метода максимума: простота технической реализации, получение наибольшего отношения сигнал-шум в момент отсчета пеленга. Недостатки метода: низкая пеленгационная чув­ствительность и, как следствие, низкая точность пеленгации.

Пеленгационная чувствительность - это способность радиопеленгатора изменять напряжение на выходе приемника при изменении положения ДН ан­тенны относительно направления на объект. Чем больше изменение напряже­ния при заданном изменении угла, тем выше пеленгационная чувствительность. Количественной мерой пеленгационной чувствительности является крутизна пеленгационной характеристики

.

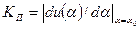Если Δu— минимальное изменение выходного напряжения приемника, которое может зафиксировать измеритель, то абсолютная погрешность измере­ния угловой координаты Δα ≈ Δu/К_п. Таким образом, чем больше крутизна пе­ленгационной характеристики, тем выше пеленгационная чувствительность и тем меньше погрешность измерения угла.

Так как максимум ДН антенны обычно «тупой», то пеленгационная чув­ствительность при пеленгации методом максимума мала и, следовательно, по­грешность измерения высока.

Пеленгация методом минимума (рис. 2.52,6) осуществляется путем плав­ного вращения ДН с резким провалом. Угол отсчитывается в тот момент, когда направление минимума пеленгационной характеристики α совпадает с направ­лением на объект α₀, при этом напряжение на выходе приемника минимально. Крутизна пеленгационной характеристики в этом случае выше, чем при методе максимума, поэтому выше и точность пеленгации. Однако амплитуда прини­маемого сигнала вблизи направления на объект мала, что затрудняет дальнометрию и, следовательно, использование метода минимума в активной радио­локации. Этот метод применяется главным образом в радионавигации при пе­ленгации источников мощного собственного излучения.

При пеленгации методом сравнения (рис. 2.52,в) угол определяется по соотношению амплитуд двух принимаемых сигналов, соответствующих двум пересекающимся диаграммам направленности f₁(α) и f₂(α). Приемник в этом случае двухканальный, причем напряжения на выходе каналов пропорциональ­ны значениям f₁(α₀) и f₂(α₀):

.

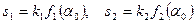Сравнивая эти сигналы, например путем деления, находим

.

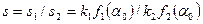Измерив отношение s и решив уравнение относительно α₀, найдем иско­мый угол. Достоинством метода сравнения является возможность быстрого оп­ределения направления на объект (в течение одного импульса) в пределах срав­нительно широкого сектора при неподвижных антеннах. Однако точность из­мерения может иногда оказаться низкой в зависимости от вида и взаимного по­ложения ДН антенн и угла прихода радиоволн.

В том случае, когда отношение сигналов s₁/s₂ стремятся сделать равным единице, приходим к равносигналъному методу пеленгации. При этом методе ДН антенной системы поворачивается до тех пор, пока объект не окажется на равносигнальном направлении РСН (см. правый рис. 2.52,в), когда s = s₁/s₂ = 1. Достоинство равносигнального метода — сравнительно высокая точность пе­ленгации, так как при измерении используется та часть ДН, которая обладает большой крутизной. Данный метод применяется при автоматическом слежении по угловым координатам за движущимся объектом. В этом случае удобнее формировать не отношение сигналов, а их разность s = s₁-s₂. Система управле­ния поворачивает антенну (или ДН при неподвижной антенне) в ту или иную сторону (в зависимости от знака величины s), стремясь свести рассогласование s к нулю. При этом равносигнальное направление будет отслеживать изменение направления на объект.

Методы сравнения, в частности равносигнальный, используют в много­канальных (моноимпульсных) радиопеленгаторах и в одноканальных. В первом случае благодаря многоканальности приемной системы сравнение сигналов происходит в один и тот же момент времени. Во втором случае нужно перио­дически менять положение ДН антенны в пространстве, при этом сравниваются между собой сигналы, принятые в разные моменты времени при различных положениях ДН. Одноканальные радиопеленгаторы проще многоканальных, од­нако менее помехозащищены и обеспечивают меньшую точность.

Фазовый метод.Фазовый метод пеленгации основан на измерении разности фаз электромагнитных колебаний, принятых на две разнесенные антенны. Пусть в точках А и В, расстояние между которыми d (рис. 2.53),

расположены приемные антенны. Разность фаз принимаемых колебаний φ_р = (2π/λ)(R_A - R_B), где R_A, R_B — расстояния от антенн до объекта. При R_A >> d, R_B >> d имеем

,

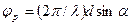где α — угол между нормалью к базе и направлением на объект. Измерив раз­ность фаз φ_р, найдем

.

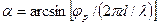При пеленгации объекта не на плоскости, а в пространстве, когда требу­ется определять две угловые координаты, нужна вторая пара антенн, база кото­рых пересекается с базой первой пары.

В качестве фазочувствительного элемента можно использовать фазовый детектор. Напряжение на его выходе пропорционально косинусу разности фаз: s = к cos φ_р. Пеленгационная характеристика u(α) = cos [(2π/λ)d sin α]. При ма­лых углах sin α ≈ α, поэтому u(α) = cos [(2π/λ)dα] (1 на рис. 2.54). Так как в окрестности α = 0 крутизна пеленгационной характеристики мала, то и точ­ность пеленгации будет низкой. Кроме того, поскольку рассматриваемая пелен­гационная характеристика является четной функцией угла, то его определение будет двузначным, т. е. нельзя будет определить направление смещения объек­та от перпендикуляра к базе.

Эти недостатки устраняются, если ввести в один из приемных каналов после резонансного усилителя РУ фазовращатель ФВ на π/2 (рис. 2.55). Напря­жение на выходе фазового детектора ФД измеряется вольтметром В. Благодаря смещению фазы сигнала в одном из каналов на π/2 пеленгационная характеристика становится нечетной функцией (2на рис. 2.54)

,

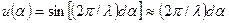при этом ее крутизна К_п = 2πd/λ. Как видим, пеленгационная чувствитель­ность, следовательно, точность пеленгации растет с увеличением отношения d/λ.Однако при этом будет умень­шаться диапазон однозначного изме­рения угла Δα_max. Действительно, по­скольку для однозначного измерения разности фаз с помощью фазового де­тектора необходимо, чтобы φ ≤ π, а при малых α согласно φ_р ≈ 2πdα/λ, то Δα_max = λ/2d.

Для обеспечения высокой точности и в то же время однозначности изме­рений можно применить многошкальный метод (подобно фазовой дальнометрии). При двухшкальном методе вводят третью антенну и создают большую и малую базы. Пара антенн с малой базой обеспечивает грубое, но однозначное измерение угла (в диапазоне Δα_max). Антенны с большой базой дают более точ­ный отсчет.

Неоднозначность пеленгации можно устранить также, применив антенны с достаточно узкими ДН: их ширина α_а не должна превышать диапазон одно­значной пеленгации, т. е. α_а ≤ Δα_max. Кроме того, остронаправленные антенны обеспечивают разрешение объектов по угловым координатам.

2.2.7. Многоканальные (моноимпулъсные) методы измерения угловых координат

Получившие широкое распространение одноканальные методы пеленга­ции, отличаясь сравнительной простотой, не всегда обеспечивают достаточную точность измерения. Основной причиной являются искажения огибающей пач­ки отраженных импульсов за счет флюктуации вторичного излучения. Этот не­достаток одноканальных методов устраняется при переходе к многоканальным. При этом для измерения каждой угловой координаты используется несколько самостоятельных приемных каналов, чаще всего два.

Многоканальные методы и системы пеленгации делят на амплитудные и фазовые. В них используются зависимости амплитуд или фаз принимаемых ко­лебаний от направления прихода радиоволн, неодинаковые для различных ка­налов приема.

На рис. 2.56 представлена простейшая двухканальная амплитудная сис­тема пеленгации. На приемные каналы поступают колебания от сдвинутых из фокуса зеркала антенны облучателей. Различным каналам соответствуют сме­щенные на некоторый угол 0см диаграммы направленности. Продетектированные импульсы с выхода приемников первого и второго каналов поступают на схему сравнения амплитуд, которая определяет их отношение. График зависи­мости отношения амплитуд от положения цели относительно оси антенной системы 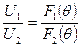для смещенных диаграмм направленности каналов F₁(θ) и F₂(θ) показан на рис. 2.57. В соответствии с этим графиком по величине отно­шения амплитуд может быть найдено смещение цели θ относительно равносигнального направления (U₁/U₂=l). Угловая координата цели θ_Ц = θ + θ₀ опреде­ляется при этом алгебраической суммой измеренной величины θ и угла пово­рота антенны θ₀, который вводится в счетно-решающее устройство.

В отличие от одноканального амплитудный двухканальный метод позво­ляет измерять угловую координату по одному принятому импульсу и вместе с другими многоканальными методами (применительно к случаю импульсного зондирования пространства) относится к классу моноимпульсных методов пе­ленгации. Наиболее важным их достоинством является нечувствительность к флюктуациям амплитуд отраженного сигнала, что для схемы рис.2.56 непосредственно вытекает из принципа их сравнения в один и тот же момент вре­мени.

Задача сравнения амплитуд облегчается, если в приемнике используются усилители с логарифмическими амплитудными характеристиками (рис. 2.58, а). Схема сравнения сводится в этом случае к вычитающему устройству, по­скольку

.

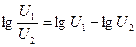Зависимость полученной величины от угла рассогласования θ (пеленгационная характеристика) показана на рис. 2.58, б. Другой способ сравнения ам­плитуд связан с использованием автоматической регулировки усиления (АРУ) колебаний промежуточной частоты обоих каналов (рис. 2.59). Если в качестве регулирующего используется одно и то же напряжение, а усилители идентич­ны, то амплитуды их выходных напряжений U_вых1=kU₁ и U_вых2=kU₂ пропорцио­нальны амплитудам входных, причем коэффициент пропорциональности (ко­эффициент усиления k) в обоих случаях одинаков. Пусть регулирующее этот коэффициент напряжение выбирается из условия практического постоянства амплитуды выходного напряжения второго канала U_вых2=c. Вэтом случае к = c/U₂, аамплитуда выходного напряжения первого канала U_вых1 = c(U₁/U₂) ока­зывается пропорциональной отношению амплитуд напряжений на входе перво­го и второго каналов.

С учетом боковых лепестков диаграмм направленности зависимость U₁/U₂ = f(θ) или lg(U₁/U₂) = φ(θ) не всегда является гладкой и монотонной, ка­кой она показана на рис. 2.57. Немонотонность этой зависимости может вести к неоднозначности измерений при U₁/U₂ » 1 или U₁/U₂ « 1. Последняя несуще­ственна, если измеряются лишь малые отклонения равносигнального направ­ления от направления на цель (U₁/U₂ ≈ 1) или если для измерения используются несколько (более двух) приемных каналов.

На рис. 2.60 показана моноимпульсная амплитудная система с рядом парциальных каналов, перекрывающих сектор обзора по одной из угловых коорди­нат, например по углу места. Сама антенная система может при этом поворачи­ваться, например, по другой координате, осуществляя обзор (сканирование). Сканирование может производиться также электрическим путем без перемеще­ния антенной системы. Продетектированные напряжения приемных парциаль­ных каналов поступают на схему сравнения амплитуд. В этой схеме направле­ние на цель грубо определяется по номеру парциального канала, выходной сиг­нал которого имеет наибольшую амплитуду. Для уточнения и устранения неод­нозначности отсчета могут использоваться значения амплитуд соседних каналов.

Решение об измеренной координате может выдаваться в результате ана­логовой или цифровой обработки. В последнем случае значения амплитуд на­пряжений на выходе канальных приемников квантуются и переводятся в циф­ровую форму.

Перейдем к рассмотрению фазовых методов многоканальной пеленгации. На рис. 2.61 показана двухканальная фазовая система пеленгации, в которой ис­пользуется разнос приемных антенн на величину d, называемую базой. Прини­маемые колебания приходят в антенны со сдвигом фаз

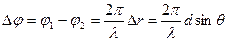
где λ —длина волны колебаний передатчика, θ — угол между направле­нием прихода радиоволн и нормалью к базе.

Далее колебания усиливаются приемниками и поступают на фазометр, который измеряет разность фаз φ₁—φ₂, зависящую от угловой координаты це­ли. Фазометр может быть проградуирован в единицах углового отклонения це­ли от нормали к базе θ, так что θ_ц – θ₀ + θ.