Обнаружение радиолокационных сигналов 6 страница

Как и амплитудная, фазовая система мно­гоканальной пеленгации позволяет определять угловое положение цели по одному принятому импульсу и относится к классу моноимпульсных. Она практически нечувствительна к флюктуациям отраженного сигнала.

Поскольку разность фаз φ₁—φ₂ определя­ется с точностью до слагаемого, кратного 2π, возможна неоднозначность отсчета. Неоднозначность устраняется за счет высокой направленности антенн, когда для углов θ в пределах главного лепестка диаграммы направленности разность фаз φ₁—φ₂ не превышает 2π. Для расширения сектора однозначного отсчета можно ввести третий антенно-приемный канал (рис. 5.66) с уменьшенной базой между ним и одним из двух других каналов. По разности фаз φ₁—φ₂ сигналов, принятых антеннами 1 и 2, угловая координата цели определяется с высокой точностью, но неоднозначно. Измерив разность фаз φ₁—φ₂ сигналов, принятых антенна­ми 2 и 3, можно устранить неоднозначность отсчета, подобно тому, как неодно­значность точного отсчета времени с помощью минутной стрелки устраняется отсчетом с помощью часовой. И в том, и в другом случае мы имеем дело с уст­ранением неоднозначности за счет многошкальных измерений.

Использование суммарно-разностных методов измерения в моноимпульсных системах

Широкое применение в моноимпульсных системах находит суммарно-разностная обработка колебаний, принимаемых различными каналами. При та­кой обработке образуются сумма и разность двух колебаний. Чтобы облегчить требования к идентичности и динамическому диапазону каналов приема, раз­дельную обработку принимаемых колебаний заканчивают схемой образования разности в самом начале приемного тракта, на высокой частоте.

Для получения суммарного и разностного колебаний обычно использу­ются высокочастотные мостовые схемы на волноводах, либо на коаксиальных линиях.

На рис.2.63 показана схема кольцевого суммарно-разностного волноводного моста. Принятые сигналы подводятся к отводам моста 1 и 2. С отвода «с» снимается суммарное колебание, а с отвода «р» — разностное. Фаза разностно­го колебания определяется фазой того из пары входных сигналов, амплитуда которого больше. Вместо кольцевого моста часто используется двойной волноводный тройник.

Суммарно-разностная обработка применяется в моноимпульсных систе­мах, основанных как на сравнении амплитуд, так и на сравнении фаз прини­маемых колебаний.

На рис. 2.64 показано подключение суммарно-разностного волноводного моста к антенной системе амплитудной моноимпульсной РЛС, измеряющей од­ну угловую координату. В этой РЛС имеются два угловых канала с неодинаковыми характеристиками направленности при общем фазовом центре. Рис. 2.65 поясняет образование суммарной и разностной диаграмм.

Колебания передатчика приходят к облучателям антенны синфазными, образуя суммарную диаграмму направленности антенны на излучение F_c(θ) = F₁(θ) + F₂(θ). Суммарная диаграмма на прием аналогична суммарной диаграмме на излучение. Зависимость раз­ностного напряжения от углового отклонения цели оп­ределяется разностной диаграммой направленности F_p(θ) = F₂(θ)-F₁(θ). При этом в соответствии со знаком углового отклонения цеди от оси системы фазы колебаний суммарного и разно­стного каналов оказываются либо одинаковыми, либо отличающимися на π, что характеризует сторону углового рассогласования. Амплитуда разностного ко­лебания при малых угловых рассогласованиях пропорциональна величине уг­лового отклонения цели.

Таким образом, разностная диаграмма направленности обладает дискриминаторными свойствами по углу и позволяет определять величину и знак уг­лового рассогласования. Для определения величины и знака рассогласования служит фазовый детектор, в котором в качестве опорного напряжения исполь­зуется суммарный сигнал. На выходе фазового детектора получаются видеоим­пульсы, полярность которых зависит от знака рассогласования. После расширения и усиления эти импульсы используются для привода исполнительного устройства следящей системы, управляющей положением антенной системы.

Для измерения угловых координат амплитудным моноимпульсным мето­дом в двух плоскостях используются две аналогичные системы с общим сум­марным каналом.

В фазовых моноимпульсных измерителях имеются угловые каналы с оди­наковыми характеристиками направленности, но разнесенными фазовыми цен­трами (см. рис. 2.61). Для измерения разности фаз мгновенных значений двух колебаний u₁(t), u₂(t) также широко используется суммарно-разностная обра­ботка. В фазометрах суммарно-разностного типа образуются сумма и разность входных колебаний, амплитуды которых одинаковы:

.

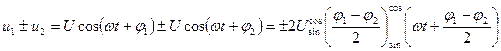Для суммирования и вычитания можно использовать, например, плечи Н и Е двойного волноводного тройника, если входные сигналы подавать в его бо­ковые плечи. Для этой же цели пригоден волноводно-щелевой мост. Суммар­ный и разностный сигналы усиливаются разными каналами, но требования к их идентичности ниже, чем при прямом измерении разности фаз.

Отношение амплитуд разностного и суммарного сигналов, которые обо­значим здесь U_- и U₊, зависит только от разности фаз исходных сигналов

,

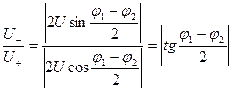что иллюстрируется на градуировочной кривой (рис. 2.66.). Как видно из ри­сунка, по отношению амплитуд U_- / U₊ можно определить разность фаз φ₁—φ₂. Однако интервал однозначного измерения разности фаз составляет в этом слу­чае только π радиан.

Интервал однозначного измерения расширяется, если использовать от­ношение мгновенных значений разностного и суммарного напряжений, пропус­тив предварительно одно из них через девяностоградусный фазовращатель. По­скольку сравниваемые колебания после этой операции приводятся к одной фа­зе, получим

,

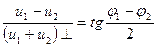где индекс _┴ указывает на операцию сдвига фазы на 90°. Из градуировочной кривой (рис. 2.67) следует, что интервал однозначного измерения расширен до 2π.

Отношение амплитуд или же мгновенных значений колебаний может быть визуально измерено с помощью осциллографа, на вертикальные и гори­зонтальные пластины которого подают продетектированные или недетектированные соответствующие напряжения.

Изображение на экране имеет вид черты, наклон которой определяется величиной отношения напряжений, а значит, и величиной измеряемой разно­сти фаз.

Автоматизированное деление амплитуд разностного и суммарного сиг­налов можно осуществить за счет использования соответствующих усилителей с быстрой автоматической регулировкой усиления.

Эффект, аналогичный делению мгновенных значений, можно получить, если после усилителей с автоматической регулировкой усиления поставить общий фазовый детектор, используя в качестве опорного напряжение суммар­ного, а в качестве основного — напряжение разностного канала (рис. 2.68). Знак напряжения на выходе фазового детектора учитывает при этом знак раз­ности фаз. В самом деле, наряду с операцией деления может быть использована операции умножения и усреднения полученного напряженияво времени:

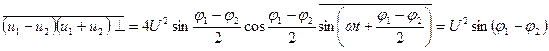
Непосредственно основанный на этом фазометр нуждается, однако, в нормировке амплитуд Uвходных напряжений за счет использования АРУ или ограничения; диапазон однозначного измерения разности фаз составляет при этом π (рис. 2.69). Если же (рис. 2.68) ввести единую автоматическую регули­ровку усиления и суммарного и разностного каналов по выходному напряже­нию суммарного, то выходной эффект умножителя будет поделен на 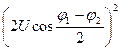. Диапазон однозначного измерения разности фаз увеличится до 2π.

Потенциальные и реальные точности двухканального моноимпульсного углового измерения

Потенциальная точность двухканального углового измерения, как и одноканального, определяется шумами и особенностями вторичного излучения цели. Наибольший интерес при этом представляет сравнительный анализ двухканальных и одноканальных систем по степени влияния этих факторов на точ­ность измерения.

Оценим ошибку углового измерения двухканальной системы, вызывае­мую шумами. Анализ проведем для антенной системы (рис.2.70) в виде двух сомкнутых излучателей с общей апертурой 2d, полагая, что отклонение на­правления на цель θ от осевого направления антенной системы мало, а величина θ определяется путем измерения разности фаз φ₁-φ₂ принимаемых колеба­ний.

В рассматриваемом случае выражение преобразуется к виду

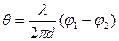
За счет влияния налагающихся на сигнал шумов фаза результирующего колебания в каждом канале отличается от фазы колебания сигнала. Считая дис­персии отклонения фазы в обоих каналах одинаковыми 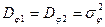, диспер­сию разности фаз представим в виде

.

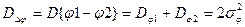Тогда дисперсия и среднеквадратичная ошибка измерения угловой коор­динаты цели будут

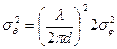и

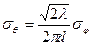
Чтобы оценить среднеквадратичное искажение фазы шумовым колебани­ем σ_φ, рассмотрим векторную диаграмму, соответствующую окрестности пика импульса и иллюстрирующую наложение шумового колебания на сигнал одно­го из каналов (рис. 2.71).

Пусть на колебание сигнала, описываемое выражением q cos ωt, наклады­вается колебание помехи ξcos ωt + ηsin ωt, причем 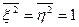. В этом случае величина q имеет смысл отношения сигнал/шум; при измерении фазы после оп­тимальной обработки значение этой величины будет 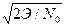. Из векторной диаграммы следует, что вызванное шумом отклонение фазы δφ при q » 1 опре­деляется величиной 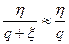, его дисперсия равна 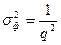, а среднеквадратичное значение .

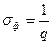Таким образом, окончательно имеем

.

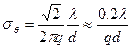Анализируя полученные результаты, убеждаемся, что двухканальные и одноканалъные системы пеленгации с оди­наковыми относительными размерами раскрыва антенн имеют практически одинаковые ошибки, вызываемые дей­ствием шумов.

Наряду с шумами на величину ошибки измерения угловой координаты влияют особенности вторичного излучения цели. Если амплитудные флюктуации сигнала в двухканальных сис­темах не сказываются, то к ошибкам могут вести флюктуации угла прихода («угловой шум») из-за несферичности фазового фронта отраженной волны.

К сказанному следует добавить, что сам по себе полураскрыв антенной системы d еще не является единственной мерой степени сложности ее реализа­ции. В частности, в случае неподвижных антенных систем его можно особенно просто увеличить, переходя к базовой системе с парой сравнительно малых антенн на краях базы.

В случае если b » d, получим

.

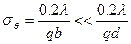При этом разрешающая способность по угловой координате не увеличи­вается, что снижает эффективность использования подобных систем в обычной активной радиолокации с пассивным ответом. Однако в случае радиолокации с активным ответом, когда вместо угловой избирательности может использовать­ся избирательность по форме ответного сигнала, подобные системы могут широко использоваться в целях повышения точности измерения угловой коорди­наты.

Для расширения рабочего сектора наряду с двухантенными измеритель­ными однобазовыми системами могут использоваться четырехантенные систе­мы с двумя взаимно перпендикулярными базами. Подобные системы измерения угловых координат могут использоваться в радиолокационных системах с ак­тивным ответом как при импульсном, так и при непрерывном ответном излуче­нии.

2.2.8. Методы измерения скорости

Измерение радиальной и путевой скоростей.Измерение радиальной скорости движения объекта сводится к измерению доплеровского смещения частоты принимаемого сигнала. Пусть, например, приемник неподвижный, а излучатель радиоволн движется и R(t) - расстояние между ними в момент вре­мени t. Радиальная скорость V_R=R(t) есть проекция вектора скорости движения излучателя на направление «приемник — излучатель». Частота f принимаемого сигнала смещена относительно частоты f₀ излучаемого на величину, равную частоте Доплера f_д = -f₀ V_R/. Отсюда радиальная скорость V_R = -cf_д//f₀. Для ее определения нужно измерить доплеровское смещение f_д, а для этого в точках излучения и приема должны быть установлены высокостабильные эталоны частоты.

В однопозиционных РЛС необходимость в указанных эталонах отпадает, так как передатчик и приемник расположены в одном месте, причем в качестве опорного колебания, относительно частоты которого измеряется смещение час­тоты принимаемого сигнала, используется сам излучаемый сигнал. Доплеров­ское смещение частоты удваивается (из-за удвоения пути, проходимого радио­волнами):

,

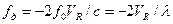где V_r = R(t) — радиальная скорость цели; R(t) — наклонная дальность. При уменьшении дальности ее производная V_R < 0 и, следовательно, доплеровское смещение f_д > 0. При удалении цели от РЛС V_R > 0, поэтому f_д < 0. Радиальная скорость

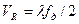
определяется в результате измерения доплеровского смещения часто­ты (рис. 2.72). Генератор высокой частоты ГВЧ формирует непрерывное немодулированное колебание частоты f₀. На смеситель См приемника поступают прямой сигнал и сигнал частоты f₀ ± f_д отраженный от цели (знак f_д определя­ется знаком V_r). В смесителе образуется сигнал биений частоты f_д, который через усилитель доплеровской частоты УДЧ поступает на частотомер Ч, проградуированный в значениях радиальной скорости.

В соответствии со структурной схемой на рис. 2.72 строят доплеровские РЛС с непрерывным смодулированным излучением. К числу досто­инств таких РЛС относятся их простота и отсутствие ближней «мертвой» зоны, благодаря чему их применяют, в частности, в радиолокационных головках на­ведения снарядов в радиовзрывателях. Важным достоинством доплеровских РЛС является их способность селектировать объекты по скорости путем на­стройки УДЧ на заданную частоту Доплера и, в частности, селектировать сиг­налы движущихся целей на фоне отражений от неподвижных объектов.

На основе схемы на рис. 2.72 строят и ДИСС, определяющие путевую скорость V и угол сноса α ЛА. Для одновременного определения V и α антенная система ДИСС должна формировать как минимум две узкие ДН, обеспечи­вающие наклонное облучение земной поверхности. При этом необходимо по­лучить достаточно большие проекции вектора скорости ЛА на направления об­лучения и то же время сохранить достаточно сильное отражение в направлении на ДИСС. Отраженные сигналы, поступающие по двум лучам, раздельно обра­батываются, измеряются их доплеровские смещения f_д1 и f_д2, однозначно свя­занные с V и α. Наибольшая точность определения путевой скорости и угла сноса обеспечивается в многолучевых ДИСС.

Измерение угловой скорости.Измеряя угловую координату движущего­ся объекта α(t), можно рассчитать его угловую скорость dα(t)/dt ≡ α(t). При неподвижных антеннах угловую скорость измеряют с помощью фазового мето­да пеленгации. Разность фаз сигналов, принятых в точках А и В (см. рис. 2.53),

.

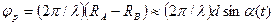Продифференцировав обе части приближенного равенства, получим

,

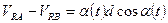где V_RA = R_a(t); V_RB = R_b(t) — радиальные составляющие скорости движения объекта. Согласно V_RA ⁼ λf_дА/2, V_RB ⁼ λf_дB/2, поэтому

.

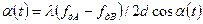При малых углах (α(t) ≤ 10°) cos α(t) ≈ 1, и тогда

.

Таким образом, измерение угловой скорости движения объекта сводится к измерению разности доплеровских частот сигналов, принятых двумя разне­сенными антеннами.

2.2.9. Методы определения местоположения объектов

Выше показано, что РЛС может измерять дальность и угловые координа­ты отражающего, излучающего или переизлучающего объекта. Естественно возникает вопрос о том, как же использовать результаты этих измерений для определения местоположения объекта.

Рассмотрим четыре метода решения этой задачи: пеленгационный, дальномерный, разностно-дальномерный и пеленгационно-дальномерный. При этом для упрощения ограничимся определением местоположения объекта на плоско­сти.

В пеленгационном методе в двух разнесенных точках А и В определяют­ся азимуты одного и того же объекта (рис. 2.73 ,а); Поскольку геометрическим местом точек, соответствующих определенному азимуту, является полупрямая (радиус), исходящая из точки измерения, то точка С пересечения полупрямых, проведенных соответственно из точек А и В под углами а₁ и а₂, и будет искомой точкой местоположения объекта.

В дальномерном методе из двух разнесенных точек А и В определяются дальности r₁ и г₂ рассматриваемого объекта (рис. 2.73,6). Так как геометриче­ским местом точек, удаленных от некоторого центра А (или В) на расстояние r₁ (или г₂), является окружность с этим центром и указанным радиусом, то точка С пересечения дуг этих окружностей покажет местоположение объекта.

В разностно-дальномерном методе (рис. 2.73, в) из двух разнесенных то­чек А и В излучаются синфазные колебания, каждое из которых принимается в некоторой точке С, где измеряется их разность фаз. Эта разность, очевидно, пропорциональна разности расстояний от точки С до соответственно точек А и В. Как известно, геометрическим местом точек, разность расстояний которых до двух фиксированных точек («фокусов») А и В факсирована, является гипер­бола. При этом каждой разности расстояний до фокусов А и В соответствует своя гипербола.

Чтобы определить местоположение объекта с помощью этого метода, нужно знать не только разность расстояний Δr` от этого объекта до точек А и В, но и разность расстояний Δr`` от этого объекта, расположенного в точке С, до другой пары точек (например, А и D). Тогда для системы фокусов А и D будет существовать гипербола, соответствующая разности расстояний Δr`` от объекта до указанных точек. Точка С пересечения этой гиперболы с гиперболой, соот­ветствующей разности расстояний Δr` объекта от фокусов А и В, ипоказывает местоположение объекта.

В пеленгационно-дальномерном методе (рис. 2.73,г) в точке О, в которой располагается система из радиопеленгатора и радиодальномера, измеряются азимут объекта а и дальность г до него. По этим координатам легко определя­ется точка С, в которой находится объект.

Сравнение этих методов показывает, что первые два из них требуют ис­пользования двух разнесенных в пространстве радиосистем (соответственно радиопеленгаторов или радиодальномеров), третий — трех разнесенных в про­странстве генераторов синфазных колебаний и трехканального радиоприемного устройства на объекте, местоположение которого определяется, а четвертый — лишь одной пеленгационно-дальномерной радиосистемы, расположенной в од­ном месте. В этом и заключается несомненное достоинство последнего, что и служит основанием для его преимущественного применения в радиолокацион­ных системах. Остальные методы в основном используются в радионавигаци­онных системах.

2.3. Разрешение сигналов

2.3.1. Понятие о разрешающей способности

Под разрешением сигналов понимают возможность раздельно обнаружи­вать и измерять параметры сигналов от близко расположенных целей. Разреше­ние сигналов неизбежно происходит на фоне шумов, которые могут сущест­венно осложнить разрешение и ухудшить его характеристики. Это объясняется тем, что выбросы шума, будучи случайными, могут принять любую форму и при взаимодействии с сигналами исказить суммарное колебание таким образом, что сигналы, разрешаемые в отсутствие шума, не будут разрешаться при его действии. Поэтому задача разрешения сигналов является статистической. Ста­тистический подход к разрешению сигналов позволяет синтезировать опти­мальные устройства разрешения, обеспечивающие потенциальную разрешаю­щую способность. Влияние шума на разрешение сигналов уменьшается по мере увеличения отношения сигнал-шум, равного, как и при обнаружении сигналов, отношению удвоенной энергии этих сигналов к спектральной интенсивности шума.

Обычно необходимость разрешения сигналов возникает при их уверенном обнаружении, когда отношение сигнал-шум достаточно велико. Однако сколь малыми не были бы шумы, именно их наличие ограничивает разрешающую способность радиосистем. Действительно при отсутствии шумов можно было бы получить сколь угодно высокое разрешение сигналов путем их пропускания через фильтр с передаточной функцией, обратной спектру сигнала. Такой фильтр носит название фильтра Урковица и рассматривается ниже. Сигналы на выходе этого фильтра представляют собой короткие импульсы, длительность которых обратная ширине полосы пропускания фильтра, и при увеличении по­следней могут обеспечить неограниченно высокое разрешение по времени (дальности).

Однако при расширении этой полосы все сильнее сказывается влияние шумов, неизбежно сопровождающих принимаемые сигналы. Мощность шумов на выходе фильтра возрастает пропорционально третьей степени указанной по­лосы. При ее расширении сокращается отношение сигнал-шум и снижается дальность действия радиосистемы. Если ограничить полосу пропускания фильтра, то импульсы сигнала на его выходе расширятся и соответственно уменьшится разрешающая способность системы по времени (дальности). Воз­никает противоречие между дальностью действия радиосистемы и ее разре­шающей способностью по дальности. Заботясь о получении высокой (разре­шающей способности радиосистемы, следует одновременно принимать ради­кальные меры и по ослаблению шумов. Как показано выше, это наилучшим об­разом достигается оптимальной фильтрацией сигналов. Определяющий разре­шающую способность радиосистемы сигнал на выходе оптимального фильтра представляет собой автокорреляционную функцию входного сигнала и целиком обусловливается формой этого сигнала.

Разрешающая способность является одной из важнейших характеристик радиосистемы. Наибольший интерес представляет разрешающая способность по следующим параметрам сигнала: временное положение, сдвиг несущей час­тоты и угол прихода электромагнитной волны, которые несут информацию со­ответственно о дальности, радиальной скорости и угловом положении цели.

Количественно разрешающая способность по некоторому параметру ц сигнала характеризуется минимальной разностью δμ = μ₁ – μ₂ двух разрешае­мых по этому параметру сигналов, имеющих одинаковые прочие параметры. Так, разрешающая способность по дальности δr равна минимальной разности дальностей двух разрешаемых точечных объектов, расположенных в одном угловом направлении и двигающихся с одинаковыми радиальными скоростями. Разрешающая способность по радиальной скорости равна минимальной разно­сти радиальных скоростей от двух разрешаемых объектов, расположенных на одной и той же дальности и в одном угловом направлении. Аналогичны

определения разрешающих способностей радиосистем по азимуту и углу места объекта.

Чтобы два сигнала υ₁(t) = υ(t,μ₁) и υ₂(t) = υ(t,μ₁) с различными пара­метрами (или совокупностями параметров) μ₁ и μ₂ были различимы в устройст­ве обработки радиосистемы, необходимо, чтобы они как можно сильнее от­личались друг от друга из-за различия параметров. Оценим это различие ин­тегральной мерой - средним квадратом их разности

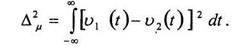
Очевидно,

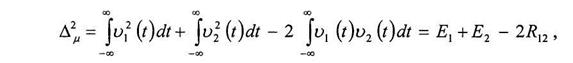
где E₁ и E₂— энергии сигналов, a R_l2— функция их взаимной корреляции. Поскольку сигналы различаются только параметром μ, который считается не­энергетическим, т. е. его изменение не влияет на энергию, то энергии сигналов одинаковы, а функция их взаимной корреляции R₁₂является их автокорреляци­онной функцией R_a (μ₁, μ₂)= R_a (Δ_μ), зависящей от разности параметров Δ_μ = μ₁-μ₂

Итак, для обеспечения высокого разрешения сигналов по параметру необ­ходимо выбирать эти сигналы так, чтобы их автокорреляционная функция уменьшалась при возможно меньшем изменении этого параметра.

2.3.2. Разрешающая способность по дальности