Обнаружение радиолокационных сигналов 2 страница
где С и t0 - постоянные.
Анализ выражения показывает, что импульсная характеристика оптимального фильтра получается из функции u(t), описывающей сигнал с нулевым временем запаздывания, путем замены в ней аргумента t на to-t. Такое преобразование соответствует зеркальному отображению функции u(f) относительно прямой 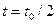 . Зеркальная импульсная характеристика оптимального фильтра обеспечивает наилучшее обнаружение сигнала на фоне белого гауссова шума. Амплитуда сигнала на выходе оптимального фильтра определяет модульное значение корреляционного интеграла, необходимое при оптимальном обнаружении сигналов со случайной начальной фазой (амплитудой и начальной фазой).
. Зеркальная импульсная характеристика оптимального фильтра обеспечивает наилучшее обнаружение сигнала на фоне белого гауссова шума. Амплитуда сигнала на выходе оптимального фильтра определяет модульное значение корреляционного интеграла, необходимое при оптимальном обнаружении сигналов со случайной начальной фазой (амплитудой и начальной фазой).
На рис. 2.7 была изображена схема канала оптимальной обработки, которая позволяет производить обнаружение сигналов с неизвестной случайной начальной фазой, отличающихся временем запаздывания.
Наряду с импульсными характеристиками фильтров широко пользуются их частотными характеристиками. Частотную характеристику K(f) линейной цепи определяют, подавая на вход цепи гармоническое колебание. Напряжение на выходе будет
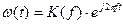
где 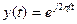 - входной сигнал.
- входной сигнал.
Частотная характеристика определится как отношение
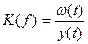 .
.
Окончательно частотная характеристика оптимального фильтра
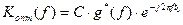 , (26)
, (26)
где С - произвольный вещественный множитель;
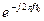 - множитель запаздывания;
- множитель запаздывания;
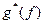 - сопряженная спектральная плотность ожидаемого сигнала.
- сопряженная спектральная плотность ожидаемого сигнала.
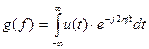 .
.
Воспользовавшись записью спектральной плотности ожидаемого сигнала g(f) через модуль и аргумент можно перейти к амплитудно-частотным и фазо-во-частотным характеристикам оптимального фильтра.
Аплитудно-частотная характеристика (АЧХ) оптимального фильтра

пропорциональна амплитудно-частотному спектру ожидаемого сигнала. Оптимальный фильтр наилучшим образом пропускает спектральные составляющие, наиболее сильно выраженные в спектре. Слабые спектральные составляющие подавляются, в противном случае наряду с ними пройдут интенсивные составляющие помехи в широком диапазоне частот. Форма амплитудно-частотного спектра на выходе фильтра искажается, что является одной из причин искажения сигнала. Однако задачей фильтрации является не точное воспроизведение формы сигнала, а наилучшее выделение его на фоне помехи.
Фазо-частотная характеристика оптимального фильтра
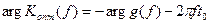
складывается из аргумента спектра ожидаемого сигнала, взятого с обратным знаком, и аргумента задержки - 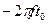 .
.
Напряжение на выходе фильтра в произвольный момент времени будет равно:
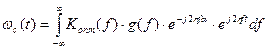 .
.
После подстановки всех составляющих получим:
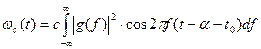 (27)
(27)
Таким образом, напряжение на выходе оптимального фильтра, являясь наложением гармонических составляющих разных частот, определяется амплитудно-частотным спектром сигнала. Оно не зависит от фазо-частотного спектра, так как последний компенсируется фазо-частотной характеристикой фильтра. Поэтому все гармонические составляющие одновременно достигают амплитудных значений в момент времени 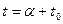 и эти значения налагаются
и эти значения налагаются

|
друг на друга (рис. 2.11). В этот момент имеет место максимум, который определяется величиной энергии входного сигнала
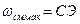 .
.
Отношение сигнал-помеха на выходе оптимального фильтра по напряжению

| Рис. 2.11. Наложение максимумов гармонических составляющих |
зависит только от энергии полезного сигнала и спектральной плотности помехи N0 и не зависит от формы сигнала.
В каждом из вариантов оптимальной обработки при обнаружении встречается вычисление корреляционного интеграла или его модульных значений. Возможен комбинированный способ вычисления, при котором используется как непосредственное перемножение напряжений, так и фильтрация полученного при этом колебания. Приемник, построенный по такому принципу, называют корреляционно-фильтровыми. Различные виды корреляционно-фильтровой обработки имеют различную степень сложности.
Рассмотрим вначале случай обнаружения когерентной пачки радиоимпульсов, но без использования линии задержки с отводами, рассчитанной на большую задержку. Ожидаемую пачку радиоимпульсов 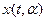 представим как произведение двух колебаний: колебания
представим как произведение двух колебаний: колебания  в виде неограниченной периодической последовательности видеоимпульсов и высокочастотного колебания
в виде неограниченной периодической последовательности видеоимпульсов и высокочастотного колебания 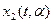 частоты
частоты 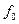 , модулированного огибающей пачки.
, модулированного огибающей пачки.
Операции взятия корреляционного интеграла

можно свести к следующим (рис. 2.12, а).
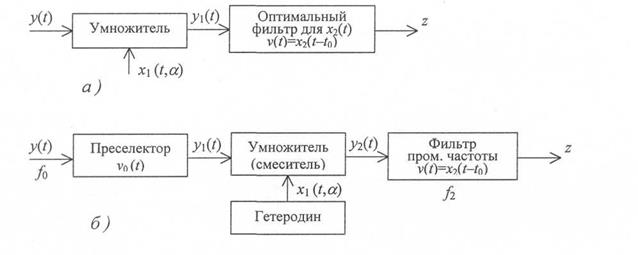
Рис. 2.12. Схемы корреляционно-фильтровой обработки
Принимаемое колебание y(f) стробируется с помощью периодической последовательности видеоимпульсов, временное положение которых соответствует принимаемой пачке. При этом получается колебание 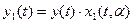 . Стро-
. Стро-
бирование практически осуществимо лишь для фиксированных значений времени запаздывания, что ограничивает возможности корреляционно-фильтровой схемы по сравнению с фильтровой.
Последующие операции умножения y1(t) на x2(t, 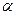 ) и интегрирования осуществляется фильтром с импульсной характеристикой
) и интегрирования осуществляется фильтром с импульсной характеристикой  . Простым приближением к такому фильтру является узкополосный контур, полоса которого обратно пропорциональна длительности пачки.
. Простым приближением к такому фильтру является узкополосный контур, полоса которого обратно пропорциональна длительности пачки.
Интегрирование может производиться не только на высокой, но и на промежуточной частоте (рис. 2.12, б). В данной схеме преселектор позволяет подавить прием по зеркальному каналу.
2.1.7. Принципы оптимальной обработки некогерентных сигналов
Некогерентными называются сигналы, фазовую структуру которых нельзя считать закономерной. Такого вида сигналы часто встречаются в обзорных радиолокаторах. В силу случайности начальных фаз, когерентное накопление возможно лишь в пределах каждого из одиночных радиоимпульсов. Накопление же от импульса к импульсу может быть только последовательным - некогерентным.
Частное отношение правдоподобия представляет собой произведение двух степенных функций: степенной функции полного корреляционного интеграла Z и степенной функции полной энергии Э пачки
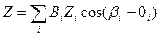 ,
,
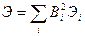 ,
,
где 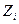 - модульное значение частного корреляционного интеграла, вычислен-
- модульное значение частного корреляционного интеграла, вычислен-
ное для случая, когда ожидаемым сигналом является г-й радиоимпульс; 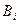 - амплитудные множители, тождественно равные единице при не-
- амплитудные множители, тождественно равные единице при не-
флюктуирующей пачке.
Для некогерентных пачек отношение правдоподобия представляет собой произведение отношений правдоподобия для одиночных радиоимпульсов соответствующего вида, т.е. со случайной начальной фазой или случайными амплитудой и начальной фазой
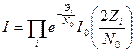
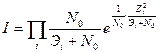
Сравнение значений отношений правдоподобия / с порогом /0 может быть заменено сравнением со своими порогами значений In/. Для рассматриваемых случаев
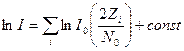 ,(28)
,(28)
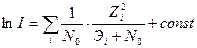 . (29)
. (29)
Оптимальные обнаружители, построенные в соответствии с соотношениями (28) и (29), вычисляют модульные значения корреляционных интегралов 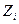 и суммируют в общем случае нелинейные функции этих модульных значений.
и суммируют в общем случае нелинейные функции этих модульных значений.
Для нефлюктуирующих некогерентных пачек суммирование логарифмов 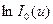 заменяется суммированием линейных или квадратичных функций величины
заменяется суммированием линейных или квадратичных функций величины 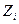 , а именно, квадратичных, если амплитуды радиоимпульсов малы по сравнению с уровнем шума,
, а именно, квадратичных, если амплитуды радиоимпульсов малы по сравнению с уровнем шума,
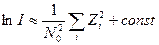
и линейных, если они велики
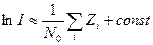 .
.
Обычно комплексные амплитуды всех ожидаемых импульсов пачки соответствуют одному и тому же закону модуляции. Они различаются только: 1) моментами прихода импульсов 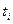 , зависящими от моментов зондирования и дальности, и 2) неслучайными множителями Si зависящими от формы огибающей пачки и угловой координаты. Поэтому все значения
, зависящими от моментов зондирования и дальности, и 2) неслучайными множителями Si зависящими от формы огибающей пачки и угловой координаты. Поэтому все значения
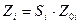
пропорциональны амплитудам некоторых однотипно получаемых видеоимпульсов 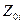 . Последние могут быть сняты с выхода единственного канала приема последовательно во времени. Достаточно, чтобы этот канал содержал схему
. Последние могут быть сняты с выхода единственного канала приема последовательно во времени. Достаточно, чтобы этот канал содержал схему
когерентной обработки для ожидаемого сигнала (оптимальный фильтр) и линейный детектор. Чтобы получить квадраты амплитуд Z\{ линейный детектор заменяется квадратичным. Рассмотренный канал приема не учитывает форму огибающей пачки радиоимпульсов и не обеспечивает последетекторное суммирование. Указанные операции реализуются в следующей схеме оптимальной обработки (рис. 2.13).
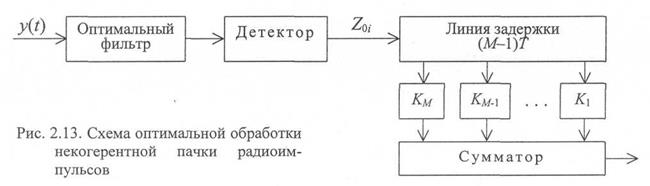
В случае слабой нефлюктуирующей пачки, когда оптимален квадратичный детектор, последовательное суммирование импульсов производится с весовыми коэффициентами 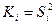 . В случае нефлюктуирующей пачки импульсов большой амплитуды оптимален линейный детектор и последовательное суммирование производится с весовыми коэффициентами Ki =Si . В случае флюктуирующей пачки оптимален квадратичный детектор и последовательное суммирование производится с весовыми коэффициентами:
. В случае нефлюктуирующей пачки импульсов большой амплитуды оптимален линейный детектор и последовательное суммирование производится с весовыми коэффициентами Ki =Si . В случае флюктуирующей пачки оптимален квадратичный детектор и последовательное суммирование производится с весовыми коэффициентами:
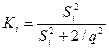 , где
, где 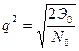 - отношение сигнал-помеха для
- отношение сигнал-помеха для
импульса с весовым множителем единица, средняя энергия которого равна Эо.
При обработке пачки отраженного сигнала определенные трудности возникают при осуществлении задержки, измеряемой длительностью пачки. В этом случае может быть использована одна линия задержки на период посылки, но за счет положительной обратной связи с выхода на вход ее превращают в рециркулятор на видеочастоте (рис. 2.9).
Широкое распространение находят схемы цифрового накопления или, иначе, схемы счета числа импульсов, превышающих порог. С учетом пропуска
отдельных импульсов из-за флюктуации или наложения противофазных шумов решение о наличии цели принимается, если налицо k и более импульсов из т возможных (критерий к/т). Для каждого т существует оптимальное значение 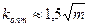 . Потери цифрового суммирования, по сравнению с квадратичным, не превышают ЗдБ.
. Потери цифрового суммирования, по сравнению с квадратичным, не превышают ЗдБ.
2.1.8. Принципы обработки широкополосных сигналов
Импульсный сигнал называется широкополосным, если произведение его длительности на ширину спектра частот 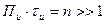 . Широкополосность
. Широкополосность
обычно достигается путем внутриимпульсной модуляции фазы (частоты) колебаний. Широкополосный импульс имеет ширину спектра в п раз большую, чем импульс той же длительности 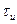 без внутриимпульсной модуляции. Ширина спектра соответствует импульсу длительностью
без внутриимпульсной модуляции. Ширина спектра соответствует импульсу длительностью 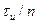 .
.
Ранее было показано, что импульс на выходе оптимального фильтра определяется амплитудно-частотным спектром сигнала. Это значит, что широкополосный радиоимпульс преобразуется в своем оптимальном фильтре в импульс такой же длительности, что и импульсы длительности 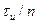 при воздействии на свой оптимальный фильтр. Иначе говоря, широкополосные радиоимпульсы сжимаются в оптимальных фильтрах, причем тем сильнее, чем больше произведение
при воздействии на свой оптимальный фильтр. Иначе говоря, широкополосные радиоимпульсы сжимаются в оптимальных фильтрах, причем тем сильнее, чем больше произведение 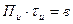 .
.
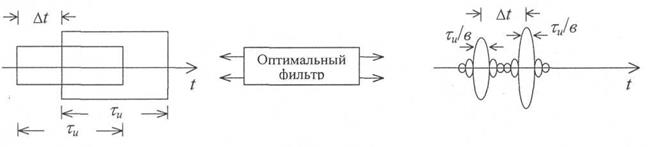
|
| Рис. 2.14. Разрешение при сжатии широкополосных радиоимпульсов в оптимальном фильтре |
Если два перекрывающихся сдвинутых широкополосных импульса воздействуют на соответствующий оптимальный фильтр (рис. 2.14), каждый из
них в силу применимости принципа суперпозиции к линейным системам сжимается независимо, т.е. имеется возможность разрешения сигналов от целей, импульсы которых перекрываются. Это позволяет наращивать длительности импульсов без ухудшения разрешающей способности по дальности. Увеличение длительности импульса является средством увеличения его энергии при неизменной пиковой мощности сигналов передатчика
 .
.
Наряду с увеличением энергии можно повышать в значительных пределах разрешающую способность по дальности, используя весьма широкополосные сигналы.
В качестве средства расширения спектра радиоимпульсов может быть применена фазовая манипуляция. Она состоит в том, что импульс длительностью 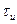 разбивается на определенное число п более коротких сомкнутых между собой парциальных радиоимпульсов, в каждый из которых вводятся фазовые сдвиги
разбивается на определенное число п более коротких сомкнутых между собой парциальных радиоимпульсов, в каждый из которых вводятся фазовые сдвиги 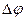 . Фазовые сдвиги могут быть кратны (или некратны) одному и тому же фазовому сдвигу, например, 2п/т, где т — целое число. При т>2 фазовая манипуляция называется многофазной, а при т=2 противофазной (возможны лишь два различных значения
. Фазовые сдвиги могут быть кратны (или некратны) одному и тому же фазовому сдвигу, например, 2п/т, где т — целое число. При т>2 фазовая манипуляция называется многофазной, а при т=2 противофазной (возможны лишь два различных значения 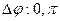 ). На рис. 2.15 изображен манипулиро-ванный по фазе 0,
). На рис. 2.15 изображен манипулиро-ванный по фазе 0,  импульс и его условное обозначение.
импульс и его условное обозначение.
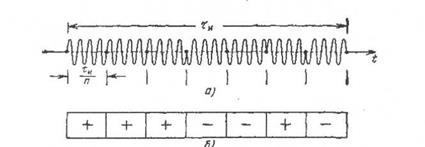
Рис. 2.15. Фазо-манипулированный радиоимпульс (а)
и его условное изображение (б)
Спектр фазоманипулированного радиоимпульса можно представить как наложение спектров сдвинутых парциальных импульсов:
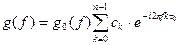 ,
,
где 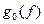 соответствует спектру первого из парциальных радиоимпульсов. В случае, когда
соответствует спектру первого из парциальных радиоимпульсов. В случае, когда 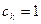 для всех к, фазоманипулированный радиоимпульс переходит в длинный немодулированный радиоимпульс.
для всех к, фазоманипулированный радиоимпульс переходит в длинный немодулированный радиоимпульс.
На рис. 2.16 изображены амплитудно-частотные спектры следующих сигналов: импульса длительности 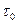 (пунктир); немодулированного импульса такой же энергии длительностью
(пунктир); немодулированного импульса такой же энергии длительностью 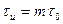 (пунктир); фазоманипулированного
(пунктир); фазоманипулированного
импульса при значениях сk, соответствующих коду + + +--+- (сплошная
линия). Ширина спектра фазоманипулированного импульса длительностью 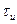 имеет тот же порядок, что и ширина спектра парциального импульса длительностью
имеет тот же порядок, что и ширина спектра парциального импульса длительностью 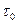 .
.
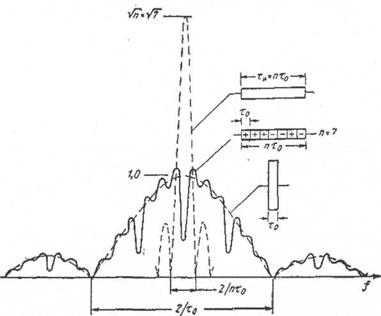
Рис. 2.16. Амплитудно-частотные спектры радиоимпульсов:
фазо-манипулированного (сплошная кривая), парциального дли-
тельностью 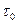 и немодулированного длительностью п
и немодулированного длительностью п 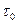 (пунктир)
(пунктир)
Другим способом расширения спектра импульса является применение частотной манипуляции. На рис. 2.17 изображен составной импульс длительно-стью 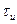 , полученный путем стыковки (с точностью до фазы) более коротких импульсов длительностью
, полученный путем стыковки (с точностью до фазы) более коротких импульсов длительностью 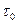 .
.

Рис. 2.17. Частотно манипулированный радиоимпульс (а) и закон изменения частоты (б) в импульсе
 Частота колебаний от импульса к импульсу меняется скачком, так что результирующий спектр складывается из взаимно смещенных парциальных спектров. Наряду со ступенчатым изменением частоты возможно плавное (линейное) изменение частоты. Радиоимпульс называется при этом частотно-модулированным (линейно частотно-модулированным).
Частота колебаний от импульса к импульсу меняется скачком, так что результирующий спектр складывается из взаимно смещенных парциальных спектров. Наряду со ступенчатым изменением частоты возможно плавное (линейное) изменение частоты. Радиоимпульс называется при этом частотно-модулированным (линейно частотно-модулированным).
На рис. 2.18 изображены закон изменения частоты внутри импульса и амплитудно-частотный спектр линейно частотно-модулированного сигнала.
Рис. 2.18. Закон изменения частоты
F(t) (а), амплитудно-частотный спектр
(сплошная линия) и его аппроксима-
ция (пунктир) при линейной частот-
ной модуляции радиоимпульса (б)
При обработке широкополосных сигналов, в оптимальных фильтрах обеспечивается их сжатие. Рассмотрим вначале процесс сжатия фазоманипули-рованного радиоимпульса длительностью 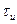 , составленного из парциальных импульсов длительностью
, составленного из парциальных импульсов длительностью 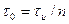 (рис. 2.19). В течение промежутка времени
(рис. 2.19). В течение промежутка времени

То частота колебаний одинакова /0, начальная фаза при переходе к очередному парциальному импульсу может изменяться скачком на п. Оптимальная импульсная характеристика схематически изображена на рис. 2.19, б. Оптимальный
Рис. 2.19. Условное изображение фильтр с такой характеристикой может быть по-
фазо-манипулированного радио- строен с использованием линии задержки с от
импульса (а) и оптимальной им- водами и сумматора, к которому часть отводов
пульсной характеристики (б) подключена через инверсные каскады (рис.2.20).
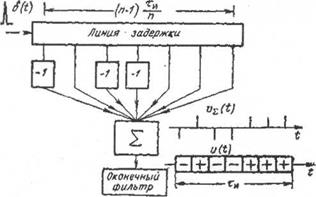
|
Рис. 2.20. Формирование импульсной характеристики, оптимальной для фазо-манипулированного радиоимпульса (рис.2.19).
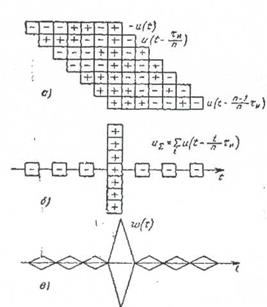
|

Рис. 2.21. Процесс оптимальной фильт- рации фазо-манипулированного радио- импульса
Выходное напряжение сумматора подается на оконечный фильтр, который является оптимальным для элементарного импульса длительностью 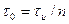 . На
. На
рис. 2.21, а схематически изображены сдвинутые во времени входные радиоимпульсы с учетом наличия инверсных каскадов. Результат суммирования изображен на рис. 2.21, б, а выходное напряжение оптимального фильтра в целом -на рис. 2.21, в. Длительность основного выброса выходного сигнала существенно меньше длительности сигнала на входе.
Рассмотрим далее обработку частотно-манипулированных радиоимпульсов. На рис. 2.22 изображена схема, позволяющая формировать такие сигналы и
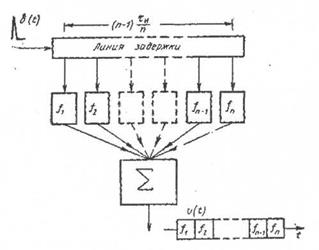
Рис. 2.22. Формирование импульсной характеристики в виде
частотно-манипулированного радиоимпульса
импульсные характеристики. Эта схема состоит из линии задержки с подключенными к ее отводам колебательным контурам и сумматора.
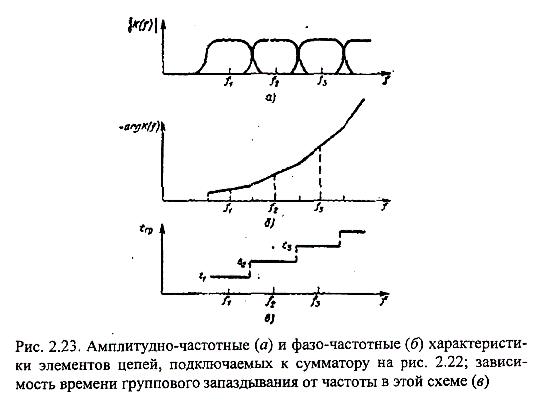
При воздействии 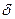 - функции на вход системы в каждом из контуров последовательно возбуждаются импульсные переходные процессы, а на выходе сумматора формируется протяженное частотно-модулированное колебание. Примерный вид амплитудно-частотной и фазо-частотной характеристик элементов цепей, подключаемых к сумматору, изображен на рис. 2.23. Фазо-частотная характеристика каждого элемента цепи определяется соответствующей задержкой и имеет тем больший наклон, чем больше эта задержка. Задержка огибающей группы близких по частоте спектральных составляющих
- функции на вход системы в каждом из контуров последовательно возбуждаются импульсные переходные процессы, а на выходе сумматора формируется протяженное частотно-модулированное колебание. Примерный вид амплитудно-частотной и фазо-частотной характеристик элементов цепей, подключаемых к сумматору, изображен на рис. 2.23. Фазо-частотная характеристика каждого элемента цепи определяется соответствующей задержкой и имеет тем больший наклон, чем больше эта задержка. Задержка огибающей группы близких по частоте спектральных составляющих
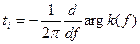 ,
,
где k(f) - фазо-частотная характеристика.
График зависимости задержки от частоты изображен на рис. 2.23, в.
Рассмотренная схема (рис. 2.22) способна осуществлять сжатие радиоимпульса, зеркального по отношении к ее импульсной характеристике.
Если от частотно-манипулированного радиоимпульса перейти к частотно-модулированному (рис. 2.24, а), то импульсная характеристика оптимального фильтра перейдет в частотно-модулированное колебание с зеркальным по отношению к сигналу законом частотной модуляции.
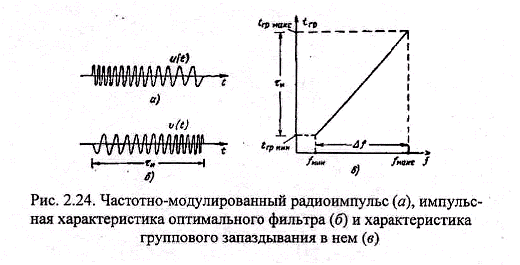
Оптимальный фильтр должен осуществлять разную задержку различных групп частот. Рисунку 2.24, б соответствует меньшая задержка низких частот и большая задержка высоких. Для этого время группового запаздывания в линии должно изменяться в диапазоне частот сигнала по определенному закону, в данном случае по линейному. Линии задержки с переменным временем группового запаздывания называют дисперсионными. Линия с характеристикой
 изображенной на рис. 2.24, е, задерживает в большей степени высокие, чем низкие частоты. Подадим на нее импульс, мгновенная частота которого изменяется от более высокой в начале до более низкой в конце импульса. Таким образом, более высокие частоты будут действовать ранее, но задерживаются в большей степени, а более низкие действуют позже, но задерживаются меньше. Это позволяет совместить все группы частот и образовать сжатый импульс.
изображенной на рис. 2.24, е, задерживает в большей степени высокие, чем низкие частоты. Подадим на нее импульс, мгновенная частота которого изменяется от более высокой в начале до более низкой в конце импульса. Таким образом, более высокие частоты будут действовать ранее, но задерживаются в большей степени, а более низкие действуют позже, но задерживаются меньше. Это позволяет совместить все группы частот и образовать сжатый импульс.
Компенсация фазо-частотного спектра сигнала является основной причиной временного сжатия, приводя к согласованному наложению гармонических составляющих и образованию пика сжатого радиоимпульса. Степень сжатия импульса полностью определяется пределами изменения частоты в импульсе (девиацией частоты)
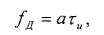
где а — скорость изменения частоты.
Длительность импульса на выходе фильтра равна:
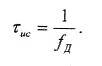
Коэффициент сжатия импульса:
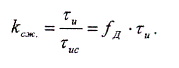
В качестве сжимающего фильтра можно использовать, например, оптимальный фильтр, состоящий из ультразвуковой дисперсионной линии задержки с полосовым корректирующим усилителем на выходе. Ультразвуковая дисперсионная линия задержки состоит из двух пьезокерамических преобразователей

 электрических колебаний в механические колебания и полоски алюминия. Время задержки такой линии зависит от частоты и в пределах частот от
электрических колебаний в механические колебания и полоски алюминия. Время задержки такой линии зависит от частоты и в пределах частот от
до изменяется линейно с частотой. Структурная схема оптимального фильтра изображена на рис. 2.25.

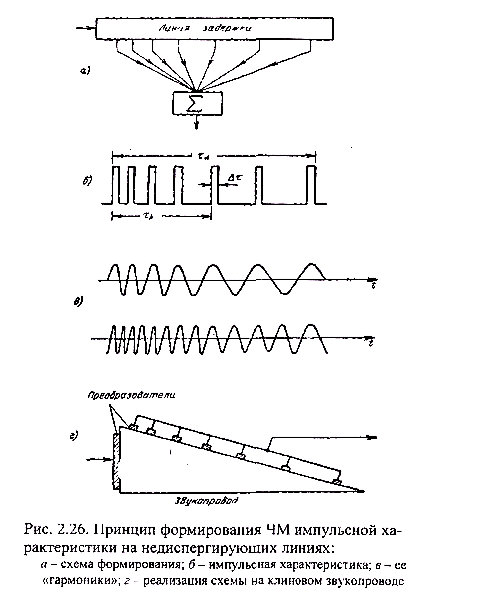
Наряду с дисперсионными ультразвуковыми и электрическими линиями задержки в качестве элементов оптимальных фильтров могут использоваться недиспергирующие линии задержки с неравномерно распределенными дискретными съемами. Принцип формирования частотно-модулированной импульсной характеристики пояснен на рис. 2.26.
Еще одним направлением построения широкополосных оптимальных фильтров является использование дисперсионных явлений на сверхвысоких частотах в так называемых магнитоупругих линиях задержки на базе кристаллов железоиттриевого граната. В таких кристаллах могут распространяться акустические и спиновые волны (волны намагничивания). Спиновые волны распространяются с групповой скоростью, зависящей от величины приложенного постоянного продольного магнитного поля и частоты распространяющихся колебаний, что позволяет создавать линии задержки с линейной дисперсионной характеристикой.
Фильтры для линейно частотно-модулированных (ЛЧМ) сигналов могут быть реализованы при использовании поверхностных акустических волн (ПАВ). Физической основой получения требуемой дисперсионной характеристики при использовании ПАВ является не дисперсия скорости волны, а пространственное разделение преобразователей, настроенных на разные частоты. Этот принцип иллюстрируется эпюрами, изображенными на рис. 2.27.

2.1.9. Ранговые обнаружители
Обнаружители, не зависящие от вида распределения, уменьшают зависимость вероятности ложной тревоги от статистического характера сигнала на входе обнаружителя. Это достигается сведением к минимуму числа допущений относительно точного характера распределения вероятности сигнала на входе обнаружителя. Качество обнаружителя в реальной ситуации зависит от того, насколько хорошо выполняются исходные допущения, принятые при его синтезе. Очевидно, чем меньше исходных допущений, тем шире круг возможных ситуаций, которые им отвечают, так что обнаружитель, не зависящий от конкретного вида распределения, наименее чувствителен к отклонениям от принятой модели. Практически это означает, что такой обнаружитель должен быть полезен в более широком кругу реальных ситуаций, чем параметрический обнаружитель.
Обнаружители, не зависящие от вида распределения, можно классифицировать несколькими способами. Эти обнаружители могут быть с фиксированными или последовательными объемами выборок и бинарными или многоальтернативными. Можно выделить следующие модели обнаружителей.
Дата добавления: 2015-06-22; просмотров: 3573;
