Обнаружение радиолокационных сигналов 1 страница
2.1.1. Качественные показатели и критерии оптимального обнаружения сигналов
Первая задача радиолокационного приема - задача обнаружения сигнала. В результате процесса обнаружения должно быть выдано решение о наличии или отсутствии цели в, произвольном разрешаемом объеме зоны обнаружения . средства радиолокации (СРЛ). Решение может быть принято при двух взаимно исключающих условиях:
условие А 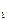 - «объект есть»,
- «объект есть»,
условие Ао - «объекта нет», которые в процессе получения решения неизвестны.
За счет помех и флюктуации полезного сигнала каждому условию могут соответствовать два вида решений:
решение А 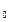 * — «объект есть»,
* — «объект есть»,
решение A* - «объекта нет»,
При обнаружении возможны четыре ситуации совмещения случайных событий «условия» и «решения»:
1) ситуация А 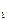 *А
*А 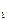 (правильное обнаружение);
(правильное обнаружение);
2) ситуация A 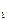 *A
*A 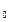 (пропуск цели);
(пропуск цели);
3) ситуация А 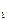 *А0 (ложная тревога);
*А0 (ложная тревога);
4) ситуация А 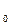 *А0 (правильное не обнаружение)
*А0 (правильное не обнаружение)
Перечисленным ситуациям соответствуют четыре вероятности совмещения событий: Р(А 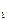 *А
*А 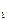 ), Р(A
), Р(A 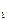 *A
*A 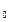 ), Р(А
), Р(А 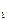 *А0), Р(А
*А0), Р(А 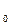 *А0). Каждому ошибочному решению ставится в соответствие некоторая плата — стоимость ошибки
*А0). Каждому ошибочному решению ставится в соответствие некоторая плата — стоимость ошибки 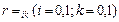 . Для безошибочных решений эта стоимость равна
. Для безошибочных решений эта стоимость равна
0 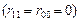 . Средняя стоимость (математическое ожидание стоимости) ошибочных решений определится следующим образом:
. Средняя стоимость (математическое ожидание стоимости) ошибочных решений определится следующим образом:
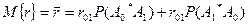 (1)
(1)
Лучшей системой обработки считается та, которая удовлетворяет критерию минимума этой стоимости - критерию минимума среднего риска. На практике переходят к условным вероятностям, являющимся качественными показателями обнаружения при условиях наличия и отсутствия объекта радиолокации.
Качественными показателями обнаружения при условии наличия объекта являются соответствующие условные вероятности правильного обнаружения
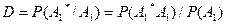 (2)
(2)
и пропуска цели
 (3)
(3)
Поскольку соответствующие одному и тому же условию 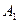 решения
решения 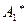 и
и 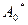 взаимоисключающие, то
взаимоисключающие, то
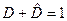
Качественными показателями обнаружения при условии отсутствия объекта являются условные вероятности ложной тревоги
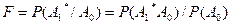 (4)
(4)
и правильного обнаружения
 (5)
(5)
причем 
Используя приведенные соотношения (2) - (5), выражение (1) для средней стоимости ошибки можно представить в следующем виде
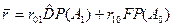
или после замены D-1-D и простых преобразований,
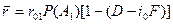 ,(6)
,(6)
где 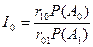
При этом критерий оптимизации обнаружения по минимуму среднего риска сводится к весовому критерию
I = D-l0F = max. (7)
Последний показывает, что по совокупности требований повышения условной вероятности правильного обнаружения D и понижения условной вероятности ложной тревоги F следует стремиться к увеличению «взвешенной» разности D- l0F. Множитель l0, называемый весовым множителем, зависит от
соотношения стоимостей ошибок каждого вида и вероятностей наличия или отсутствия объектов в исследуемом участке пространства. Дать рекомендации по выбору D и F затруднительно. Допустимые значения условных вероятностей правильного обнаружения и ложной тревоги обычно устанавливают из практических соображений.
Оптимизация обнаружителей может достигаться одновременным уменьшением условных вероятностей ложной тревоги и пропуска цели. В таких обнаружителях оба вида ошибок нежелательны в одной и той же степени. Поэтому полагают 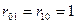 и средний риск приобретет смысл суммарной вероятности ошибки (Рош)
и средний риск приобретет смысл суммарной вероятности ошибки (Рош)
| Условие минимума этой вероятности (Рош = min) носит название критерия идеального наблюдателя. Ложная тревога является опасным явлением, ибо может вызвать крайне нежелательные, а порой и необратимые, последствия. Увеличение вероятности ложной тревоги не может быть допущено даже за счет снижения вероятности пропуска сигнала. Если обнаружитель максимизирует разность D- l0F, то фиксация F влечет за собой максимизацию вероятности правильного обнаружения D. Следовательно, оптимальный обнаружитель обеспечивает наибольшую, среди всех обнаружителей, вероятность правильного обнаружения D и |
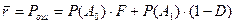 .
.
Фиксированном значении вероятности ложной тревоги F. Это является основой критерия Наймана – Пирсона.
Обычно значения априорных вероятностей Р(А0) и Р(А1) заранее неизвестны. Наибольшую информативность, в этом случае, обеспечивает равенство этих вероятностей Р(А0) = Р(А1) = 0,5. Тогда вероятность суммарной ошибки
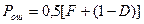 .
.
Условие минимума вероятности ошибочного решения
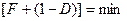
носит название критерия максимального правдоподобия.
В радиолокации наибольшее применение находит критерий Неймана -Пирсона. При этом основными качественными показателями радиолокационного обнаружения являются условные вероятности правильного обнаружения D и ложной тревоги F.
2.1.2. Оптимизация обнаружения
Обнаружитель сигнала решает задачу выяснения следующего: содержит принимаемое колебание отраженный сигнал или нет. На вход обнаружителя поступает колебание у, которое при отсутствии сигнала представляет собой шум п, а при наличии сигнала - сумму шума и сигнала (п+х). В общем случае входной сигнал можно записать в такой форме
у = п + Ах ,
где неизвестный дискретный параметр А принимает значение 0 или 1. Таким образом, задача сводится к тому, чтобы по измеренной величине у дать оценку этого параметра А*, оптимальную с точки зрения критерия минимума среднего риска или эквивалентного ему весового критерия.
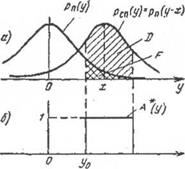
Полагаем, что величины х, у и п за время наблюдения не меняются. Ожидаемое значение сигнала х точно известно. Закон распределения случайной величины п также известен (будем полагать его нормальным). На рис. 2.1 изображены графики плотностей вероятности случайной величины у при условиях отсутствия сигнала А=А0 =0 и его наличия A=A1=1:
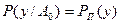 ,
,
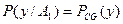 .
.
Индексы «П» и «СП» указывают на наличие одной помехи или наличии сигнала с помехой. Кривая РСП (у) сдвинута по отношению к кривой РП (у) на постоянную величину х.
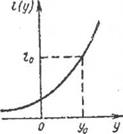
Рис. 2.1. Условные плотности вероятности РП (у) и РСП (у) и график решающей функции А*(у)
Любое закономерное решение задачи обнаружения может быть описано решающей функцией А* = А*(у), которая в зависимости от реализации у принимает одно из двух значений: 0 или 1. Из графика решающей функции следует, что для y0<y<y1принимается решение о наличии сигнала. Условные вероятности D и F имеют смысл вероятностей попадания случайной величины у в интервал 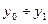 при условии «сигнал + помеха» или «помеха» и соответствуют заштрихованным областям на рисунке. Для произвольной решающей функции выражения для D и F можно записать в виде интегралов в бесконечных пределах
при условии «сигнал + помеха» или «помеха» и соответствуют заштрихованным областям на рисунке. Для произвольной решающей функции выражения для D и F можно записать в виде интегралов в бесконечных пределах
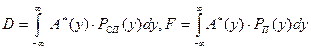 (8)
(8)
Выражение D- l0F, соответствующее весовому критерию, может быть представлено следующим образом
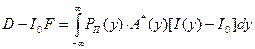 (9)
(9)
где 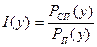 (10)
(10)
Согласно весовому критерию оптимальной является такая система обнаружения, которая обеспечивает максимум интеграла (9). Чтобы выполнить это условие, достаточно добиться для каждого у наибольшего значения подынтегрального выражения за счет выбора решающей функции А*(у). Эта функция
принимает только два значения: 0 или 1, так что подынтегральное выражение либо обращается в 0, либо умножается на 1. Поэтому полагаем:
1) А*(у)=1, если подынтегральное выражение положительное;
2) А*(у)=0 в противном случае.
Поскольку плотность вероятности РП (у) не может принимать отрицательных значений, то оптимальное правило решения задачи обнаружения может быть записано в виде
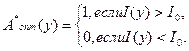 (11)
(11)
Величина 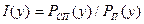 называется отношением правдоподобия. Оно характеризует, какую из гипотез следует считать правдоподобной. Отношение правдоподобия не может выражаться отрицательным числом. Решение о наличии сигнала принимается, если отношение правдоподобия превышает пороговую величину l0, в противном случае принимается решение об отсутствии сигнала.
называется отношением правдоподобия. Оно характеризует, какую из гипотез следует считать правдоподобной. Отношение правдоподобия не может выражаться отрицательным числом. Решение о наличии сигнала принимается, если отношение правдоподобия превышает пороговую величину l0, в противном случае принимается решение об отсутствии сигнала.
В случае, если помеха описывается центральным гауссовым распределением со стандартным отклонением n0и дисперсией 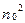 , отношение правдоподобия будет равно
, отношение правдоподобия будет равно
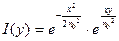 (12)
(12)
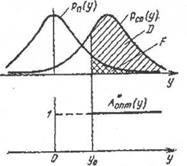
Зависимость l(y) для х > 0 изображена на рис. 2.2.
При х>0 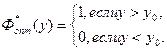
Величина у0 называется порогом. При заданном уровне помех условная вероятность ложной тревоги F зависит только от величины у0:
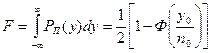 , (13)
, (13)
где 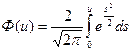 - интеграл вероятности.
- интеграл вероятности.
Таким образом, величину порога можно выбирать непосредственно по заданному уровню вероятности ложной тревоги, что соответствует критерию Неймана-Пирсона.
|
|
Рис. 2.2. Зависимость отно- Рис. 2.3. Условие плотности веро-
шения правдоподобия от ре- ятности Рп (у), РСП (у) и график ре
зультатов наблюдения шающей функции А*опт (у)
Условная вероятность правильного обнаружения определится следую-
щим образом:
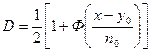 (14)
(14)
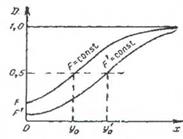
При заданном уровне помех n0 величина D зависит не только от порога у0, но и от величины ожидаемого сигнала (рис. 2.4). Зависимость D(x) может быть построена качественно из анализа площади под кривой РСП (у) на рис. 2.3 и количественно в соответствии с выражением (14). Чем выше уровень порога у0
и меньше условная вероятность ложной тревоги F, тем больше кривая D(x)
сдвигается вправо.
|
При этом для обеспечения той же вероятности D требуется больший уровень полезного сигнала. Кривые, изображенные на рис. 2.4 называются кривыми обнаружения.
Рис. 2.4. Кривые обнаружения
2.1.3. оптимальное обнаружение полностью известного сигнала
Будем полагать, что ожидаемый сигнал x(t, а) полностью известен, т.е. известны его форма, амплитуда, временное положение и т.д. Обнаружитель должен выработать решение о наличии или отсутствии сигнала. На вход обнаружителя поступает сигнал y(t), который обнаруживается на фоне белого гауссов- ского шума n(t).
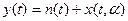
Отношение правдоподобия для этого случая может быть представлено в следующем виде
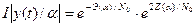 ,(15)
,(15)
где 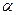 - фиксируемый при обнаружении параметр или совокупность параметров ожидаемого сигнала;
- фиксируемый при обнаружении параметр или совокупность параметров ожидаемого сигнала;
N0 — спектральная плотность шума; Э( 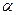 ) - энергия ожидаемого игнала; Z(
) - энергия ожидаемого игнала; Z( 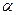 ) - корреляционный интеграл
) - корреляционный интеграл
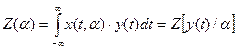 .(16)
.(16)
Отношение правдоподобия является монотонной функцией корреляционного интеграла, который может быть рассчитан по принятой реализации y(t) для любого фиксированного параметра 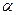 . Сравнение отношения правдоподобия с порогом l0 эквивалентно сравнению корреляционного интеграла с соответствующим порогом z0.
. Сравнение отношения правдоподобия с порогом l0 эквивалентно сравнению корреляционного интеграла с соответствующим порогом z0.
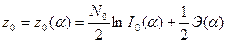 .
.
Таким образом, оптимальный обнаружитель должен вычислять корреляционный интеграл (16) и сравнивать его с порогом. Структурная схема простейшего обнаружителя сигнала с полностью известными параметрами изображена на рис. 2.5.
Величина корреляционного интеграла сравнивается с порогом z0. Уровень порога подбирается так, чтобы вероятность F ложного превышения порога

Рис. 2.5. Простейший корреляционный обнаружитель
была не больше допустимой. Опорное колебание x(t, 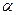 ) может вырабатываться специальным гетеродином или получаться непосредственно от передатчика путем задержки сигнала на время
) может вырабатываться специальным гетеродином или получаться непосредственно от передатчика путем задержки сигнала на время 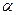 .
.
2.1.4. Оптимальное обнаружение сигнала со случайной начальной фазой
Обычно сигнал, принимаемый приемником, неизвестен точно. Как правило, его амплитуда, начальная фаза, время запаздывания и другие параметры заранее неизвестны. Возможны два способа приема сигналов с неизвестными параметрами. Первый способ предполагает предварительное измерение всех его неизвестных параметров и последующий прием как полностью известного сигнала. Этот способ требует выделения специального времени на выполнение указанных выше измерений, усложнения аппаратуры и значительной величины отношения сигнал-шум. Этот способ может быть заменен другим, при котором неизвестные параметры сигнала считаются случайными, а его прием ведется без учета конкретных значений параметров путем статистического усреднения принятого колебания.
Методика определения отношения правдоподобия для сигналов со случайными нефиксированными параметрами по принятой реализации y(t) сводится:
1) к вычислению корреляционного интеграла, энергии ожидаемого сигнала и
частного отношения правдоподобия при фиксированных параметрах 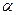 и
и 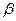 (
( 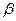 —
—
случайный нефиксированный при обнаружении параметр или совокупность па-
раметров: начальная фаза, амплитуда);
2) к усреднению частного отношения правдоподобия по случайному нефикси
рованному параметру 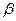 .
.
Для указанной выше ситуации частное отношение правдоподобия определится следующим образом:
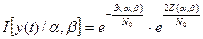 ,(17)
,(17)
где Z 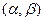 и Э
и Э 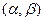 - частные значения корреляционного интеграла и нергии сигнала.
- частные значения корреляционного интеграла и нергии сигнала.
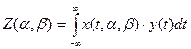 (18)
(18)
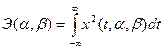 .(17)
.(17)
Ведя речь о фазовой структуре сигналов, следует определиться с когерентностью. Когерентными называют сигналы с закономерной фазовой структурой, однако начальная фаза 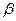 радиолокационного сигнала обычно является неизвестной случайной величиной. Такой сигнал может быть представлен в виде:
радиолокационного сигнала обычно является неизвестной случайной величиной. Такой сигнал может быть представлен в виде:
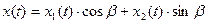 ,(20)
,(20)
где  .
.
sin
Тогда частное значение корреляционного интеграла (18) приводится к виду:
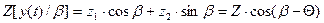 ,
,
где 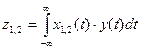 ,
,
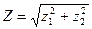 ,
,
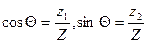
Для сигнала, содержащего большое число периодов колебаний, частное значение энергии от 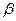 не зависит
не зависит 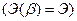 .
.
Учитывая, что все случайные начальные фазы равновозможны, полагаем их распределение равномерным в пределах от 0 до 2 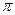 с плотностью вероятности
с плотностью вероятности 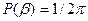 . Определяя математическое ожидание частного отношения правдоподобия и вводя модифицированную функцию Бесселя первого рода нулевого порядка
. Определяя математическое ожидание частного отношения правдоподобия и вводя модифицированную функцию Бесселя первого рода нулевого порядка 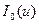 , получим
, получим
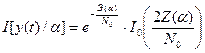 (20)
(20)
где Z 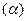 - модульное значение корреляционного интеграла, определяемое для принятой реализации y(t) с учетом фиксированного параметра а
- модульное значение корреляционного интеграла, определяемое для принятой реализации y(t) с учетом фиксированного параметра а
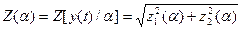 (22)
(22)
Таким образом, для сигнала с неизвестной начальной фазой отношение правдоподобия является монотонной функцией модульного значения корреляционного интеграла. Структурная схема оптимального обнаружителя сигнала со случайной начальной фазой изображена на рис. 2.6.
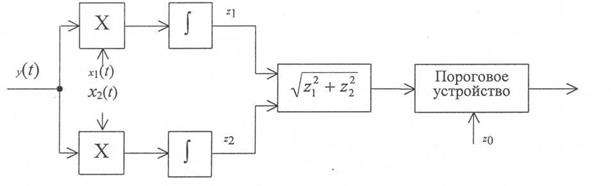
Рис. 2.6. Структурная схема оптимального обнаружителя сигнала со случайной фазой
Характеристики обнаружения сигнала со случайной начальной фазой имеют тот же вид, что и при точно известном сигнале, но лежат несколько правее, что свидетельствует о проигрыше в отношении сигнал—шум.
Если реализуется прием одиночного сигнала со случайной начальной фазой, простейшая схема оптимального обнаружителя имеет вид, изображенный на рис. 2.7.

Рис. 2.7. Оптимальный приемник для обнаружения сигнала с неизвестной начальной фазой
Согласованный фильтр такой, у которого коэффициент передачи K 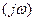 есть величина, комплексно сопряженная спектру S
есть величина, комплексно сопряженная спектру S 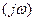 сигнала. Импульсная переходная характеристика согласованного фильтра с точностью до постоянного множителя является зеркальным отражением входного сигнала на оси времени. Такой фильтр обеспечивает максимальное отношение сигнал-шум.
сигнала. Импульсная переходная характеристика согласованного фильтра с точностью до постоянного множителя является зеркальным отражением входного сигнала на оси времени. Такой фильтр обеспечивает максимальное отношение сигнал-шум.
Если принимается последовательность импульсных сигналов со случайной начальной фазой, то выбор схемы обнаружителя существенно зависит от взаимосвязи фаз отдельных сигналов. При когерентной пачке импульсных сигналов (имеет место функциональная зависимость фазы колебаний от времени) оптимальный приемник может быть реализован в соответствии со структурной схемой, изображенной на рис. 2.8.
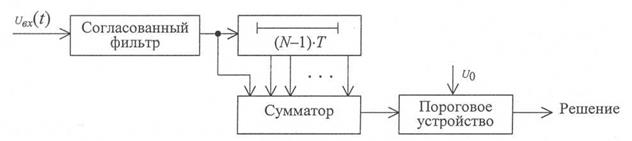
Рис. 2.8. Оптимальный приемник для обнаружения пачки когерентных импульсов одинаковой амплитуды и длительности
Согласованный фильтр в данной схеме является оптимальным для отдельного импульса пачки. Линия задержки имеет (N-1) отводов (N — число импульсов в пачке). Если период следования импульсов Т, то общая задержка в линии равна (N-l)-T. В момент окончания пачки импульсов на выходе сумматора имеет место наибольшее значение отношения сигнал-шум, характеризуемое суммарной энергией пачки импульсов.
Для некогерентной пачки импульсов (начальные фазы отдельных импульсов статистически независимы) оптимальный приемник принимает вид, изображенный на рис. 2.9.
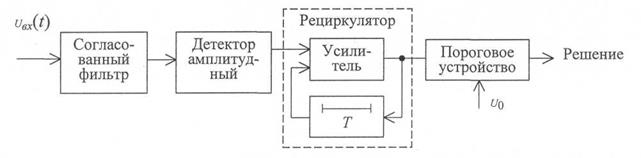
Рис. 2.9. Оптимальный приемник для обнаружения пачки одинаковых некогерентных импульсов
Приемник включает: фильтр, согласованный с одиночным импульсным сигналом; детектор амплитудный; рециркулятор, используемый для накопления видеоимпульсов; пороговое устройство. Рециркулятор имеет коэффициент передачи меньше единицы, вследствие чего накопление импульсов происходит неоптимальным образом и поэтому схема на рис. 2.9 является квазиоптимальной.
В момент окончания пачки импульсов отношение сигнал-шум на выходе рециркулятора имеет максимальное значение. Суммирование импульсных сигналов происходит после нелинейного элемента - детектора амплитудного, который ухудшает отношение сигнал-шум на выходе по сравнению с этим отношением до детектора. Вследствие этого, результирующее отношение сигнал-шум некогерентной пачки импульсов оказывается меньшим, чем у когерентной.
2.1.5. Оптимальное обнаружение сигнала со случайными амплитудой и начальной фазой
Часто случайной бывает не только начальная фаза, но и амплитуда, что приводит к дальнейшему ухудшению характеристик обнаружения по сравнению с полностью известным сигналом. Для этого случая сигнал может быть записан следующим образом:
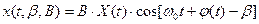 .
.
Для такого сигнала частное отношение правдоподобия при фиксированном В будет равно
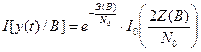
где Z(b) = BZ, Э(B) = В2Э; Э и Z - энергия и модульное значение корреляционного интеграла, рассчитанные по ожидаемому сигналу, соответствую-
щему В=1.
При этом величина Э выбирается равной средней энергии
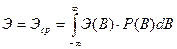 .
.
Задаваясь релеевским распределением амплитуд
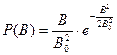
окончательно получим:
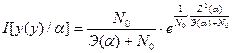 (23)
(23)
Для сигнала с неизвестными амплитудой и начальной фазой отношение правдоподобия является монотонной функцией модульного значения корреляционного интеграла Z( 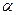 ), как и в случае, когда неизвестна только начальная фаза. Совпадение алгоритмов обнаружения позволяет использовать в обоих случаях одинаковые схемы обработки.
), как и в случае, когда неизвестна только начальная фаза. Совпадение алгоритмов обнаружения позволяет использовать в обоих случаях одинаковые схемы обработки.
Особенность характеристик обнаружения в рассматриваемом случае состоит в том, что с ростом отношения сигнал-шум вероятность обнаружения возрастает сначала быстро, а после достижения значений D = 0,5 - 0,6 это увеличение замедляется, а затем становится очень медленным. Это объясняется тем, что при действии таких сигналов изменяются лишь параметры распределения Релея величины Z в оптимальном обнаружителе.
На рисунке 2.10 изображены кривые обнаружения для различных сигналов.
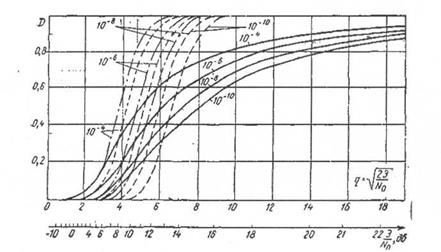
Рис. 2.10. Кривые обнаружения для сигналов: с полностью известными параметрами (штрих-пунктир), со случайной начальной фазой (пунктир), со случайными амплитудой и начальной фазой (сплошные линии)
Приведенные выше схемы являются оптимальными лишь тогда, когда положение ожидаемого сигнала на оси времени известно. Ответ о наличии сигнала с неизвестным временем запаздывания может быть дан, если установить факт его наличия или отсутствия для различных значений времени запаздывания. Приходим, таким образом, к необходимости многоканальных корреляционных схем, что является недостатком при реализации алгоритмов обнаружения в радиолокации.
Для одноканальной обработки радиолокационной информации могут быть применены фильтровые и корреляционно—фильтровые системы.
2.1.6. Принципы фильтровой и корреляционно—фильтровой обработки сигналов
Считая вначале параметры сигнала известными полностью, потребуем,
чтобы элемент схемы оптимального приема вычислял корреляционный инте
грал для произвольного времени запаздывания ожидаемого сигнала 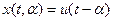 .(24)
.(24)
Тогда корреляционный интеграл будет
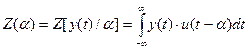 ,(25)
,(25)
откуда видно, что схема вычисления корреляционного интеграла должна осуществлять операцию интегральной свертки. Для реализации математической операции (25) можно использовать фильтр, который будем называть оптимальным или согласованным фильтром.
Одной из основных характеристик произвольного линейного фильтра является его импульсная характеристика, которая описывает реакцию системы на входное воздействие в виде единичного импульса, поданного в момент времени t=0. Импульсная характеристика оптимального фильтра описывается следующим выражением:
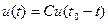 ,
,
Дата добавления: 2015-06-22; просмотров: 8659;
