Обработка сигналов в условиях воздействия импульсных помех

2.6.1. Обработка сигналов в условиях воздействия
несинхронных импульсных помех

При работе РЛС могут заметно сказываться взаимные импульсные помехи. Различают несинхронные и синхронные взаимные импульсные помехи. Несинхронные помехи образуются, если периоды повторения импульсов мешающего источника не совпадают с периодом повторения полезных сигналов. На индикаторах с большим послесвечением несинхронная помеха при большой разнице в периодах повторения создает эффект наличия большого числа целей. По мере сближения частот повторения, изображение несинхронной помехи на экране индикатора принимает вид спирали. При полностью синхронном излучении спирали вырождаются в окружности. В этом случае говорят о синхронной помехе.

Признаком, по которому несинхронную помеху можно отличить от цели, является иной, чем у цели, интервал между соседними импульсами. Существует ряд способов, позволяющих исключить из обработки помеховые сигналы. Наиболее употребительны два способа, базирующиеся на регулярности отраженных сигналов от ВС и случайным временным положением сигналов несинхронных импульсных помех (НИП). Первый способ основан на рециркуляции задержки сигналов, второй - на эффекте «движущееся окно». Рассмотрим оба
способа обработки.

Несинхронные помехи образуются, если периоды повторения мешающего источника не совпадают с периодом повторения сигналов от ВС. Следовательно, различительным признаком сигнала и помехи является интервал между соседними импульсами. Для ослабления НИП может быть использовано перемножение незадержанных и задержанных на период следования сигналов в схеме селекции по периоду следования (рис. 2.146). Если перемножение осуще-

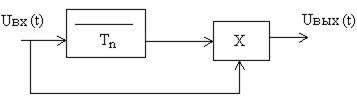
Рис. 2.146. Схема селекции по периоду следования.

ствляется на видеочастоте, через схему пройдут сигналы, имеющие известный период повторения Т_n, и не пройдут сигналы, для которых период следования отличается от Т_n. В таких схемах могут быть применены потенциалоскопы.

Разновидностью устройства селекции по периоду следования может являться следующее (рис. 2.147).

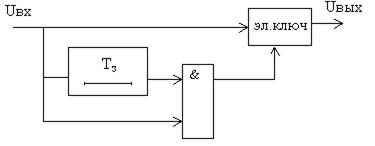
Рис. 2.147. Простейший подавитель НИП

В течении первого периода зондирования на выход электронного ключа обрабатываемый сигнал не походит, поскольку нет разрешающего сигнала со схемы совпадений. Входной сигнал первого зондирования запоминается устройством задержки на время периода повторения Т_n. В момент излучения следующего зондирующего импульса вновь поступает принятый сигнал, который непосредственно приходит на схему совпадений одновременно с сигналом от устройства задержки. В моменты прихода полезных сигналов, повторяющихся в соседних периодах зондирования, на выходе схемы совпадений появляется
разрешающий импульс, благодаря чему открывается электронный ключ и пропускает на выход схемы импульс цели.

В данной схеме реализован алгоритм 2/2, то есть, если имеется 2 сигнала в одном и том же дискрете дальности на текущем и предшествующем периодах зондирования, то принимается решение о том, что это сигнал цели. Значительно большей эффективностью обладают подавители, реализующие алгоритм 4/4.

Еще один вариант схемы селекции по периоду повторения - рециркуля-
тор, который осуществляет и функцию накопления сигнала. Схема такого устройства изображена на рис. 2.148.

На вход рециркулятора поступают нормированные сигналы полезные и
НИП. Цепь обратной связи образована линией задержки на время Т_n и усилителем b(K_ус.< 1).

Суммарный сигнал на выходе накопителя

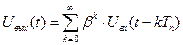
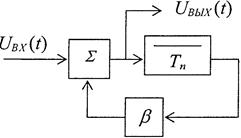
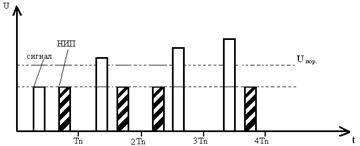
Рис. 2.3. Рециркулятор и графики, поясняющие его работу.

Сигналы от ВС регулярны, следуют через Т_n и будут накапливаться на
выходе накопителя. Период следования сигналов НИП отличается от Т_n и такие сигналы накапливаться не будут. Дальнейшая пороговая обработка исключает сигналы НИП и выделяет накопленные сигналы от ВС.

Метод "скользящего окна" заключается в следующем. Зона обнаружения первичной РЛС разбита по дальности на отдельные дискреты DД (рис.2.149).

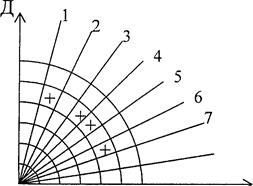
Рис. 2.149. Скользящее окно.

На рисунке показана только часть обзора, причем увеличены для наглядности временные промежутки между соседними зондированиями (они обозначены цифрами 1, 2, ...). При наличии сигналов в каком-либо дискрете дальности они будут обнаружены в соответствующих ячейках (сигналы обозначены +). Дальнейшая обработка предполагает проверку критерия "k/m". Если в данном дискрете дальности в окне, включающем т соседних зондирований, находится l ³ k: входных сигналов, делается вывод о том, что это не случайный набор, а упорядоченная группа сигналов (пачка импульсов от ВС). Если l становится меньше k (сигналы НИП), то критерий не выполняется и сигналы исключаются из обработки.

2.6.2. Обработка сигнала на фоне шума и сигнальных импульсных помех

2.6.2.1. Понятие о динамическом диапазоне сигналов и помех
и необходимости их нормирования

Системы обработки сигналов на фоне шума и помех должны обеспечить заданный уровень вероятности правильного обнаружения при фиксированной вероятности ложных тревог. Последние вызываются как выбросами шума, так и импульсными и иными помехами. Импульсные помехи очень распространены и часто по своему уровню значительно превосходят полезные сигналы, что затрудняет их надежное выделение. Поэтому приходится использовать нелинейные и иные методы обработки сигналов на фоне шумов и помех. Простейшим и весьма эффективным из них является амплитудное ограничение. Обычно ограничитель выбирается жестким, т. е. уровень ограничения выбирается меньше среднеквадратического значения s шума. При его применении уровни сигнала, шума и помехи становятся одинаковыми. Чтобы уменьшить искажения сигналов, после амплитудного ограничителя ставят фильтр, выделяющий его первую гармонику.

Поскольку ограничитель устраняет все амплитудные различия между
сигналом, шумом и помехами, последующая обработка должна использовать
иные различия между сигналом, с одной стороны, и шумом и помехами, с другой. Если применяются простые сигналы, то такими различиями могут быть или длительности их импульсов, или ширина их спектров, определяемая этими длительностями, а в случае сложных сигналов — их фазовая структура, т. е. законы фазовой модуляции или манипуляции.

Очевидно, требуемые характеристики работы радиосистемы будут гарантированы, если обеспечить высокое отношение сигнал-шум и малое отношение помеха-шум. Поскольку импульсные помехи могут быть очень сильными, их уровень необходимо нормировать к среднеквадратическому уровню шума. Иначе говоря, необходимо обеспечить высокий динамический диапазон сигналов и нормирование динамического диапазона помех.

Под динамическим диапазоном сигналов понимается отношение уровней максимального и минимально различимого сигналов. Последний определяется уровнем шума, характером сигнала и применяемым алгоритмом его обработки. Поэтому динамический диапазон сигналов можно характеризовать отношением амплитуды максимального сигнала к среднеквадратическому уровню шума.

Аналогично динамический диапазон помехи описывается отношением
амплитуды максимальной помехи к среднеквадратическому уровню шума. Поэтому нормирование динамического диапазона помех сводится к нормированию уровня этих помех. В дальнейшем под помехой будем понимать немодулированную импульсную помеху, частота которой совпадает с частотой сигнала. При этом будет рассматриваться самый неблагоприятный с точки зрения подавления помехи случай, поскольку спектры сигнала и помех полностью перекрываются, что исключает применение частотной фильтрации. Амплитуды помехи и сигнала будем считать столь большими относительно среднеквадратического уровня шума, что в течение их действия на ограничитель влиянием шума можно пренебречь.

Заметим, что в данной главе, как это и следует из ее названия, рассматривается только внутрипериодная обработка сигналов на фоне шума и сильных импульсных помех. Дальнейшее подавление импульсных помех возможно путем череспериодного накопления сигналов в процессе их межпериодной обработки на фоне шума и указанных помех и достигается вследствие несинхронного характера импульсных помех.

2.6.2.2. Нормирование уровня длинных импульсных помех
с помощью схемы ШОУ

Схема ШОУ (рис. 2.150,а) состоит из широкополосного фильтра Ш, ограничителя О, узкополосного фильтра У. Рассмотрим воздействие на нее радиоимпульсного сигнала длительностью t₁ шума и помехи длительностью t_п1. Пренебрегаем искажениями сигнала и помехи в широкополосном фильтре, что вполне допустимо при его большой полосе. Узкополосный фильтр будем считать оптимальным для сигнала. Тогда отношение сигнал-шум на его выходе

,

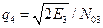где Ез — энергия сигнала на входе этого фильтра;

N₀₃ — спектральная интенсивность шума на его входе.

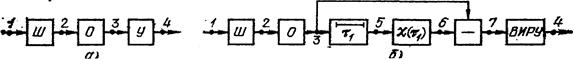
а б

Рис. 2.150. Схема ШОУ (широкая полоса - ограничитель-узкая полоса)

При идеальном ограничении входного колебания (рис. 2.151) выходное
колебание имеет вид меандра, принимающего значения ±Uо. При этом энергия сигнала на выходе этого ограничителя (т.е. на входе узкополосного фильтра) Ез= 1/2 V² _зt₁ =1/2(a₁U₀)²t₁, а спектральная интенсивность шума N₀₃=W_ш3/DF_ш=1/DF_ш х 1/2(a₁U₀)², где a₁= 4/p — коэффициент первой гармоники образовавшегося при ограничении колебания в виде меандра, а W_ш3— мощность шума на входе узкополосного фильтра. Подставляя два последних выражения в им предшествующее, получаем

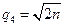
где n = DF_ш t₁@ DF_ш / DF_у — отношение полос пропускания широкопо-
лосного и узкополосного фильтров.

Чем больше это отношение, тем больше отношение сигнал-шум на выходе рассматриваемой схемы. Физически это объясняется тем, что с расширением полосы широкополосного фильтра уменьшается спектральная интенсивность шума после ограничения и мощность после узкополосной фильтрации.

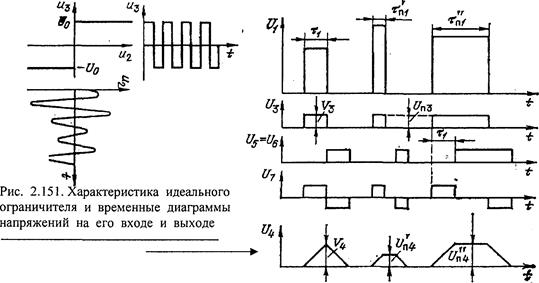
Рис. 2.152. Прохождение сигнала,
короткой и длинной помех через схему
ШОУ

Рассмотрим прохождение радиоимпульсов сигнала, короткой и длинной помех (различающихся тем, что длительности короткой помехи t¢_п1 меньше, а длинной помехи t"_п1больше длительности сигнала t₁ через систему ШОУ, в качестве узкополосного фильтра которой применяется оптимальный фильтр для импульсного сигнала указанной длительности.

Анализ временных диаграмм амплитуд напряжений (рис.2.152) в различных точках структурной схемы (рис. 2.150, б) показывает, что сигнал,
короткая и длинная помехи имеют соответственно амплитуды напряжений на выходе системы

V₄=1/b V₃t_1,

U¢_п4=1/b U_п3t_п1,

U"_п4=1/b U_п3t_1,

где (b — постоянная времени контура ВИРУ, связанная, с его полосой
пропускания DF соотношением b = (pDF)^-1, причем b » t₁ и b » t_п1 , а V₃ и U_п3
— амплитуды сигнала и помех на выходе ограничителя. Ввиду равенства последних (V₃ = U_п3) амплитуды сигнала и длинной помехи совпадают:

V₄= U"_п4, а амплитуда короткой помехи U¢_п4⁼ V₄ (t¢_п1 /t₁).

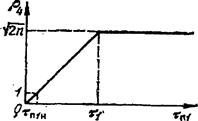
рис. 2.153. Зависимость отношения помеха-шум на выходе схемы ШОУ от длительности входной помехи

Все это — следствие того, что совокупность задерживающего и вычитающего устройств в оптимальном фильтре ограничивает время интегрирования любого входного колебания длительностью t₁ сигнала на входе.

Следовательно, если длительность помехи равна или больше длительности сигнала, то ее амплитуда на выходе узкополосного фильтра совпадает с амплитудой сигнала. Если же длительность помехи меньше длительности сигнала, то ее амплитуда и отношение помеха-шум пропорциональны длительности помехи.

Таким образом, отношение помеха-шум на выходе (рис. 2.153)

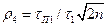При t_п1≤t₁

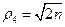При t_п1>t₁

Важно отметить, что уровень помехи на выходе совершенно не зависит
от ее амплитуды на входе (если она, конечно, достаточно велика). Схема ШОУ осуществляет селекцию импульсных помех по длительности. Помеха нормируется к уровню шума (r₄£1), если ее длительность удовлетворяет условию

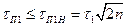
Следовательно, схема ШОУ защищает только от достаточно коротких настроенных импульсных помех.

С точки зрения лучшего нормирования помех, а также уменьшения числа взаимных помех, создаваемых радиосистемами с близкими несущими частотами, которые попадают в полосу пропускания предограничительного
фильтра, отношение n следует выбирать меньше. Но при этом уменьшается отношение сигнал-шум, а следовательно, и вероятность обнаружения сигнала. Кроме того, при уменьшении n увеличиваются потери из-за нелинейности обработки, обусловленные уменьшением степени нормализации шумов в узкополосном фильтре после ограничения. Расчеты показывают, что если при n =100 они составляют 1,5 дБ, то при n=10 возрастают до 5 дБ. На практике динамический диапазон сигналов выбирают q = 5 ¸ 10 из условия нормальной работы индикатора кругового обзора, что соответствует n = 12,5 ¸ 50.

2.6.2.3. Нормирование уровня длинных импульсных помех
с помощью схемы РОС

Схема РОС (расширяющий фильтр — ограничитель — сжимающий фильтр) работает по принципу: расширение сигнала Р - ограничение О- сжатие сигнала С и представляет собой последовательное соединение двух
дисперсионных линий задержки ДЛЗ с сопряженными (т. е. различающимися знаками) фазо-частотными характеристиками и ограничителем между ними (рис. 2.154). Полосы пропускания ДЛЗ DF₁ выбираются равными ширине спектра полезного сигнала (на уровне 2/p): DF₁= П=1/t₁, а длительность Т_p импульсной характеристики значительно больше длительности сигнала, т. е.

Т_p» t₁.

Сигнал, действуя на первую ДЛЗ, расширяется по длительности до Т_p и приобретает ЛЧМ с девиацией DF= П. Он становится сложным, ибо произведение его ширины спектра на длительность

D_p=П Т_p = Т_p /t₁»1,

где D_p — коэффициент растяжения сигнала в ДЛЗ. После прохождения
ограничителя он, будучи сложным, сжимается во второй ДЛЗ до прежней длительности 1/DF = t₁), а его амплитуда увеличивается в 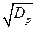раза по сравнению с амплитудой на выходе ограничителя, которая совпадает с амплитудой окружающего шума. Поэтому отношение сигнал-шум.

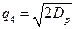
Прохождение помехи через рассматриваемую систему существенно зависит от ее длительности t_п1. Ее спектр на уровне 2/p имеет ширину П₁=1/t_п1 (см.рис. 2.155,а). Так как полоса пропускания ДЛЗ составляет лишь DF₁=1/t₁, то ширина П₂ спектра короткой помехи на ее выходе ограничивается этой величиной (см. рис. 2.155,6):

П₂=DF₁= 1/t₁, При t_п1<t₁,
П₂= 1/t_п1 При t_п1 ³t₁

При t_п1>t₁ весь спектр помехи (на уровне 2/p) попадает в полосу пропускания ДЛЗ, которая вследствие своей дисперсионности задерживает различные гармонические составляющие на разное время, определяемое дисперсионной характеристикой этой ДЛЗ. Время задержки наиболее сильно различается на крайних (максимальной и минимальной) частотах спектра помехи. Разность этих временных задержек определяет длительность импульса помехи t_п2 на выходе, которая, как это следует из подобия треугольников abc и deg на дисперсионной характеристике ДЛЗ (рис. 2.156), составляет

t_п2 = Т_p П2/DF₁ = Т_p t₁/t_п1

и уменьшается с увеличением t_п1 (рис. 2.15 5,в). Последние физически объясняется сужением спектра помехи. Но длительность импульса на выходе

растягивающего фильтра не может быть меньше длительности импульса на

входе: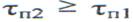

Минимальную величину 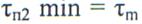определим из условия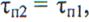
из которого следует

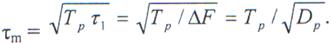
При действии более длительной помехи 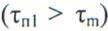последняя не меняет
своей длительности.

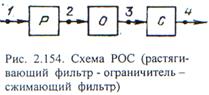
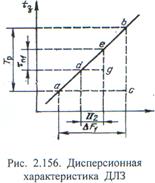
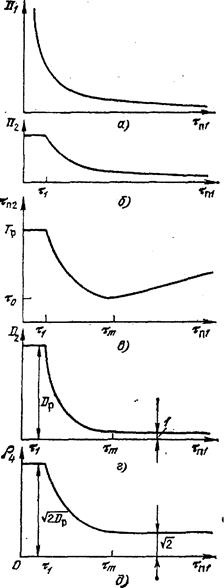
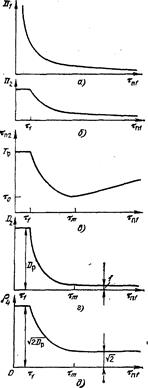Рис. 2.155. Зависимости параметров помехи от ее длительности в схеме РОС

Итак, величина Тm является минимально возможной длительностью импульсной помехи на выходе ДЛЗ. Кроме того, она представляет собой длительность основного переходного процесса на выходе ДЛЗ (т. е. оптимального фильтра для ЛЧМ сигнала с длительностью Тр и девиацией частоты ар]), вызванного действием достаточно длинной немодулированной настроенной импульсной помехи.

Итак, величина Тщ является минимально возможной длительностью импульсной помехи на выходе ДЛЗ. Кроме того, она представляет собой
длительность основного переходного процесса на выходе ДЛЗ (т. е. оптимального фильтра для ЛЧМ сигнала с длительностью Тр и девиацией частоты ар]), вызванного действием достаточно длинной немодулированной настроенной импульсной помехи.

Из предыдущего следует, что коэффициент сложности D2 помехи на выходе первой ДЛЗ, т. е. произведение ее ширины спектра П2 на длительность 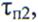, зависит от длительности помехи следующим образом (рис. 2.15 5,г):

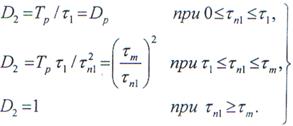
Поэтому после прохождения ограничителя, который сделает равными

т < т
уровни помехи и шума, помеха во второй ДЛЗ при 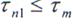сожмется по длительности в D2 раз, увеличится по амплитуде в 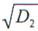раз и при этом в 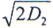раз превысит среднеквадратическое значение шума. При иной длительности помеха пройдет через ДЛЗ, не меняя амплитуды и длительности. Таким образом, отношение помеха-шум на выходе составляет (рис. 2.155, д).

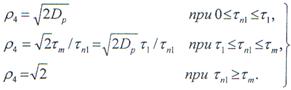
Следовательно, помехи, длительность которых превосходит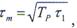
нормируются рассматриваемой схемой к уровню шума. Физически это объясняется тем, что столь длительные помехи, обладая сравнительно узким спектром, проходят через обе ДЛЗ, не подвергаясь растяжению и сжатию. Поэтому после ограничения они становятся на уровне шума. Таким образом, схема РОС осуществляет селекцию импульсных помех по ширине спектра.

Итак, если схема ШОУ нормирует уровень коротких импульсных помех, то схема РОС — уровень длинных импульсных помех. Возникает естественное стремление совместить достоинства обеих схем в единой системе обработки.
Эта возможность и рассматривается ниже.

2.6.2.4. Нормирование уровня коротких и длинных помех
с помощью схемы ШОУ-РОС

Для нормирования уровня как коротких, так и длинных импульсных помех целесообразно применить систему ШОУ—

РОС — совокупность последовательно соединенных схем ШОУ и РОС (рис. 2.157). Комбинацию РОС—ШОУ, образованную в результате другой последовательности соединения указанных схем, использовать не имеет смысла, так как в схеме РОС полоса пропускания равняется ширине спектра полезного сигнала и использование широкополосного фильтра последнее будет бесполезным.

Приближенный анализ прохождения сигнала, шума и импульсных помех [12], выполненный для случая, когда отношение п полос пропускания фильтров схемы ШОУ совпадает с коэффициентом Dр растяжения сигнала в первой ДЛЗ схемы РОС (п-Dр), позволяет получить следующую зависимость отношения помеха-шум на выходе системы ШОУ—РОС от длительности помехи на ее входе:

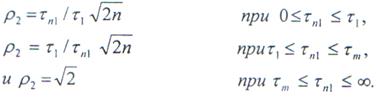
Анализ этой зависимости (рис. 11.9) показывает, что указанная система
нормирует уровень как коротких, так и длинных импульсных помех к уровню шума.

2.6.2.5. Нормирование уровня импульсных помех
при обработке сложных сигналов

В качестве сложного сигнала возьмем сначала ЛЧМ импульс. Оптимальный фильтр для такого сигнала состоит из полосового фильтра ПФ и дисперсионной линии задержки ДЛЗ, которая фактически выполняет функции фазового компенсатора ФК. Пусть этот фильтр располагается после ограничителя, которому предшествует лишь широкополосный фильтр (рис. 2.159, а).

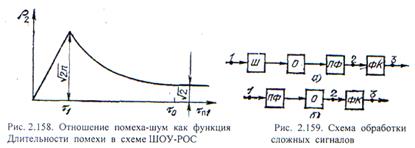
Поскольку полосовой фильтр можно рассматривать в качестве узкополосного, то схема до фазового компенсатора представляет собой схему ШОУ с шириной полосы «узкополосного» фильтра 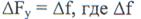—девиация частоты ЛЧМ сигнала. Поэтому на ее выходе, т. е. на входе фазового компенсатора, отношение сигнал-шум составляет 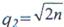, а отношение помеха-шум

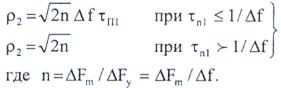
Амплитуда ЛЧМ сигнала увеличивается в ДУЛЗ фазовом компенсаторе в
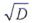раз, а мощность шума не претерпевает изменений. Поэтому на выходе фазового компенсатора отношение сигнал-шум составляет 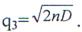При длительности помехи 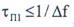меньшей длительности сжатого в ДЛЗ ЛЧМ

импульса, длительность ее на выходе полосового фильтра равна 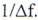. На выходе ДЛЗ помеха в этом случае расширяется до длительности ЛЧМ импульса 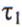а ее амплитуда уменьшается в 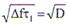раз. Поэтому

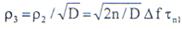
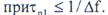
При длительности помехи, меньшей длительности переходного процесса

в ДЛЗ 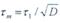, помеха расширяется в ДЛЗ до 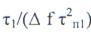и амплитуда ее на

выходе уменьшается в 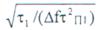раз. В этом случае (при ) отношение помеха-шум составляет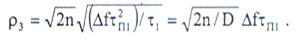

При 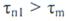помеха проходит через ДЛЗ, не изменяя своей длительности и амплитуды. Поэтому отношение помеха-шум на выходе ДЛЗ совпадает с этим отношением на выходе полосового фильтра, которое равно

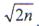
Следовательно, отношение помеха-шум на выходе

Поскольку 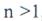, отношение помеха-шум будет меньше единицы, если ее
длительность удовлетворяет условию

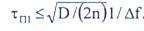
Это условие нормирования помехи к уровню шума.

Далее пусть сложным сигналом является рассмотренный ФМ сигнал общей длительности Ть составленный из радиоимпульсов длительностью 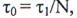, которые различаются временным положением и могут различаться начальной фазой 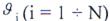Последняя принимает одно из двух значений: 0 и π. Тогда полосовой фильтр ПФ на схеме (см. рис. 2.159, а), который будем считать «узкополосным», представляет собой оптимальный фильтр для радиоимпульса длительностью 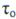, а фазовый компенсатор ФК —
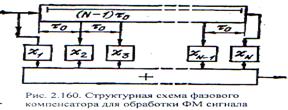
совокупность линии задержки на время 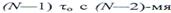равномерно расположенными отводами, N фазовращателей на угол 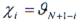и сумматора (рис. 2.160). Тогда на входе фазового компенсатора, как_на выходе схемы ШОУ,отношение сигнал-шум составит , а отношение помеха-шум

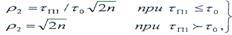
где в данном случае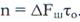

Шум после прохождения полосового фильтра, являющегося оптимальным фильтром для радиоимпульса длительностью 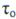, будет иметь треугольную АКФ с шириной основания 2 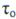. Поэтому шумы на входах сумматора не коррелированы и суммируются в нем по мощности, ввиду чего .
Поскольку сигнал возрастает в фазовом компенсаторе в N раз по амплитуде и в
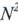раз по мощности, то отношение сигнал-шум на его выходе составит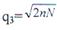

Помеха малой длительности 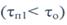растягивается полосовым фильтром
до длительности То элементарного импульса, а если длительность помехи превышает указанное значение, то фильтр оставит ее без изменения.

Поэтому при помехи на .входах сумматора могут накладываются друг на друга только фронтами, что не приведет к увеличению амплитуды помехи на выходе. Вследствие этого и того, что мощность шумов возрастает, отношение помеха-шум на выходе фазового компенсатора уменьшится в 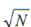раз:

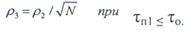
Если длительность помехи не менее длительности сигнала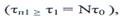
то помехи на входах сумматора будут перекрываться, вследствие чего амплитуда помехи на выходе будет больше в 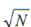раз, чем на входе. Суммирование помех по мощности, а не по напряжению объясняется квазислучайным законом изменения коэффициентов передачи фазовращателей, который обусловлен псевдослучайным характером используемого кода. Вследствие того, что в данном случае и помеха, и шум возрастают в одинаковой степени, их отношения
не меняются: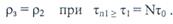

По-видимому, в промежуточном случае 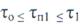имеем

Отношение помеха-шум на выходе

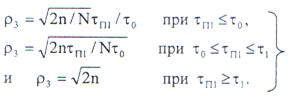
Поскольку при 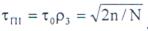отношение помеха-шум не больше
единицы, если длительность этой помехи удовлетворяет условию

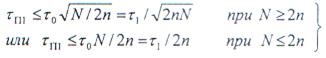
Это условие нормирования помех к уровню шума. Оно выполняется только для
достаточно коротких помех.

Таким образом, рассматриваемая система обработки (см. рис.
2.159,а) с оптимальной фильтрацией после ограничения нормирует к уровню
шума только достаточно короткие импульсные помехи. В этом и заключается
ее существенный недостаток, который объясняется тем, что помехи, ограниченные до уровня шума в ограничителе, накапливаются в узкополосном поло-
совом фильтре. Поэтому устранить указанный недостаток можно только путем
ликвидации этого накопления (интегрирования) помех.

Поскольку совсем убрать полосовой фильтр ПФ невозможно, ибо
он осуществляет абсолютно необходимую оптимальную частотную фильтрацию сигналов от шумов, то поставим его перед ограничителем

(см. рис. 2.159, б). При таком построении схемы необходимость в применении широкополосного фильтра отпадает. Указанный полосовой фильтр осуществляет первую основную операцию оптимальной фильтрации — частотную фильтрацию. Вторая операция — компенсация фазовых сдвигов между спектральными составляющими сигнала — производится фазовым компенсатором. Полоса пропускания последнего может быть неограниченно большой.
Поэтому накопление помех (и сигналов) в нем можно полностью устранить, ввиду чего его вполне можно поставить после ограничителя.

Рассмотрим действие сигнала, помех и шумов на систему, в которой полосовой фильтр предшествует ограничителю, а фазовый компенсатор стоит после него (см. рис. 2.159,6).

Так как уровни сигнала, шума и помехи на выходе ограничителя
одинаковы, то отношение сигнал-шум и отношение помеха-шум составляют

В случае ЛЧМ сигнала его амплитуда увеличивается фазовым компенсатором в 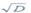раз, а уровень шума остается неизменным. Поэтому отношение
сигнал-шум на выходе В случае ФМ_сигнала его амплитуда возрастает в фазовом компенсаторе в 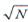раз, а среднеквадратическое значение шума

— в N раз, ввиду чего отношение сигнал-шум на выходе .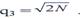

Как следует из предыдущего, фазовый компенсатор может только оставить без изменения или даже уменьшить отношение помеха-шум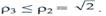

Следовательно, система обработки сложного сигнала, состоящая из узкополосного полосового фильтра, ограничителя и широкополосного фазового компенсатора, позволяет нормировать к уровню шума импульсные помехи любой длительности. В этом и заключается ее несомненное достоинство. Она реализует одно из основных преимуществ системы со сложными сигналами ее помехозащищенность, обусловленную сложной фазовой структурой этих сигналов.