Классический метод анализа линейных цепей

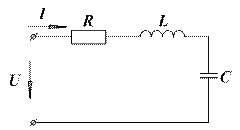
Рассмотрим применимость классического метода на конкретных примерах. Пусть к цепи (двухполюснику), показанной на рис. 1.3,а, приложено напряжение, изменяющееся по гармоническому закону:

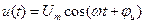, (1.1)

где U_m – амплитуда, 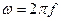– круговая частота, 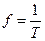– частота, Т – период, 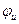– начальная фаза напряжения.

Требуется установить зависимость между напряжением и током в цепи. Для этого составим уравнение по второму закону Кирхгофа:

,

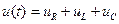где

; ; .

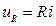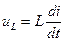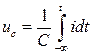а)	б)

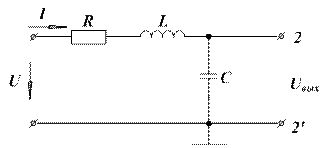
Рис. 1.3. Последовательная RLC цепь: а – двухполюсник; б – четырехполюсник

Функцию (1) можно записать в следующем виде

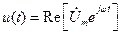, (1.2)

где 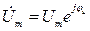– комплексная амплитуда напряжения;

Re – оператор, указывающий, что u(t) равно реальной (вещественной) части показательной формы записи комплексной величины.

Применяя формулу Эйлера для выражения в скобках:

,

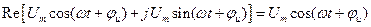получаем из (1.2) выражение (1.1).

Аналогично этому представлению запишем выражение для тока в цепи

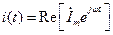, (1.3)

где 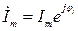– комплексная амплитуда тока,

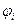– начальная фаза тока.

С учетом представления напряжения и тока в комплексной форме записи: 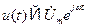; 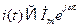, – второе уравнение Кирхгофа примет следующий вид:

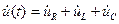(1.4)

где точка сверху означает комплексную величину:

; ; ; .

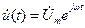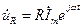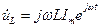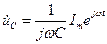С учетом формы записи величин, входящих в выражение (1.4), получаем

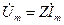, (1.5)

где 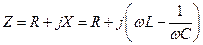(1.6)

полное сопротивление цепи (импеданс цепи).

Выражение (1.5) есть закон Ома в комплексной форме записи. При выводе этого выражения временной множитель сократился, остались только комплексные амплитуды. При необходимости временной множитель 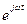может быть всегда восстановлен.

Полное сопротивление представим в показательной форме записи:

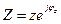(1.7)

где 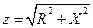– модуль полного сопротивления;

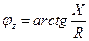– аргумент полного сопротивления.

С учетом (1.7) выражение (1.5) запишем в виде:

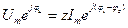. (1.8)

Если в выражении (1.6) Х = 0, то цепь имеет активный характе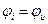р и . При

Х ≠ 0 в показателе выражения (1.8) появляется слагаемое 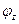характеризующее реакцию цепи на приложенное напряжение. С учетом этого замечания выражение (1.8) запишем в виде:

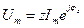. (1.9)

Умножив обе части выражения (1.9) на временной множитель 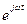, перейдем к вещественной форме записи через оператор Re[]:

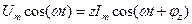. (1.10)

В выражении (1.10) начальный фазовый сдвиг тока в цепи обусловлен реакцией цепи на приложенное напряжение, то есть наличием индуктивности и емкости. Если в цепи нет индуктивности, то Х имеет отрицательное значение и ток отстает по фазе от приложенного напряжения. Если в цепи нет емкости. то Х имеет положительное значение и ток опережает по фазе приложенное напряжение. В общем случае Х зависит от частоты, и цепь имеет индуктивный характер в области частот 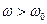и емкостной характер в области частот 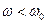, где 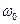– резонансная частота, при которой

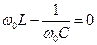
и равна

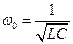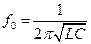, . (1.11)

Следовательно, на резонансной частоте 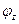= 0 и цепь имеет активный характер, при этом между приложенным напряжением и током в цепи нет фазового сдвига.

Изложенный метод получения выражения (1.5) называется методом комплексных амплитуд.

Рассмотренная в качестве примера на рис. 1.3,а цепь является цепью второго порядка. Порядок этой цепи определяет дифференциальное уравнение

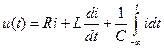
или

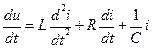. (1.12)

На рис. 1.3, б та же цепь представлена в виде четырехполюсника. При известном токе в цепи напряжение на выходе равно:

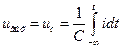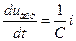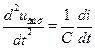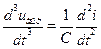; ; ; . (1.13)

С учетом (1.13) выражение (1.12) запишем в виде:

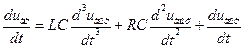(1.14)

В общем случае любая сложная цепь описывается следующим дифференциальным уравнением:

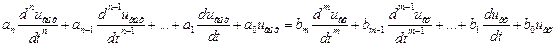. (1.15)

Для линейных цепей все коэффициенты a_n,…a₀; b_m…b₀ – вещественные постоянные величины.

Будем полагать, что u_вх – заданный входной сигнал. Тогда правая часть выражения (1.15) известна. Следовательно, анализ отклика (реакции) линейной цепи на известное входное воздействие сводится к решению линейного дифференциального уравнения n-ого порядка.

К линейным цепям применим принцип суперпозиции, суть которого в следующем: выходной сигнал на сложное (суммарное) воздействие равен алгебраической сумме выходных сигналов на простые воздействия, на которые раскладывается сложное воздействие. В математической форме этот принцип записывается так:

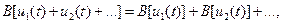(1.16)

где В – оператор, характеризующий реакцию линейной цепи на входной сигнал.