Связь энергии сигнала с полосой пропускания

Для определения энергии сигнала воспользуемся выражением (1.29):

.

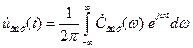Интегрируя квадраты модулей левой и правой частей в интервале 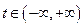, получаем величину пропорциональную энергии сигнала

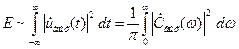. (1.34)

Зависимость 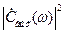называется энергетическим спектром. Она характеризует распределение энергии сигнала по частотам его спектра:

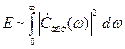. (1.35)

Если ограничить интегрирование в выражении (1.35) то отношение

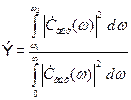(1.36)

показывает, какая часть энергии сигнала на выходе цепи сосредоточена в полосе пропускания. Если величина Э задана, то из выражения (1.36) можно определить полосу пропускания.

Средний квадрат напряжений тепловых шумов определяется формулой Найквиста:

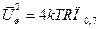, (1.37)

где 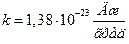– постоянная Больцмана,

Т – абсолютная температура, R – сопротивление,

П_0,7 – полоса пропускания.

Отношение энергии спектра на выходе цепи к энергии шумов на единичном сопротивлении определяется выражением

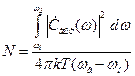. (1.38)

Из выражения (1.38) следует, что полоса пропускания линейной цепи должна определяться по максимуму отношения сигнала к шуму.

Для оценки отношений (1.36) и (1.38) необходимо рассмотреть некоторые детерминированные сигналы и их спектры. Следует заметить, что реальные сигналы, несущие информацию, имеют случайный характер и отличаются от детерминированных, которые будут рассматриваться. Однако, рассмотрение конкретных примеров позволит представить из каких соображений ограничивается энергетический спектр сигнала.