ОПРЕДЕЛЕНИЕ ПРИРАЩЕНИЯ ЭНТРОПИИ ПРИ ПЛАВЛЕНИИ ТВЕРДОГО ТЕЛА

Закон сохранения энергии устанавливает взаимопревращаемость различных видов энергии, но не указывает направленность этих процессов. Все виды энергии можно перевести в теплоту, однако теплота может быть превращена в другие виды энергии только с помощью специальных машин. При этом часть теплоты обязательно теряется, т.е. невозможен механизм, который все получаемое от нагревателя количество теплоты целиком переводил бы работе, часть этого количества теплоты должна быть отдана холодильнику. Это одна из формулировок второго начала термодинамики.

Коэффициент полезного действия (кпд) тепловой машины определяется выражением:

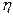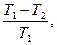= где

Т₁ – температура нагревателя;

Т₂ – температура холодильника

Отсюда видно, что коэффициент полезного действия тепловой машины тем больше, чем больше разность температур нагревателя и холодильника. Практически невозможно превратить в работу огромное количество тепла, содержащееся в воде морей и океанов, так как разность температуры окружающих тел и воды незначительна.

Для оценки «качества» теплоты в этом отношении, а также для количественного учета обесценивания и рассеивания теплоты в термодинамике пользуются величиной, которая называется приведенной теплотой:

Q_пр= ,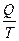

Т.е. это количество теплоты, приходящееся на один градус Кельвина.

Важной характеристикой является изменение приведенной теплоты при различных процессах. Если приведенная теплота возрастает, это значит, что возможности полезного использования теплоты уменьшилось и наоборот.

Однако в термодинамике чаше пользуются величиной, получившей название энтропии S , которая выражается через приведенные теплоты:

,

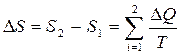т.е. разбивают весь процесс на достаточно малые участки и суммируют, считая, что температура в пределах каждого из этих участков постоянная. Тогда S₁ и S₂ – энтропия в начальном и конечном состояниях системы, а 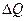- теплоты, сообщаемое или отнимаемое от системы на элементарном участке.

Другая формулировка второго начала термодинамики следующая: энтропия термодинамических систем однозначная функция состояния этих систем.

Функцией состояния называется такая физическая характеристика системы, изменение которой при переходе системы из одного состояния в другое не зависит от вида соответствующего этому переходу термодинамического процесса, а целиком определяется значениями параметров начального и конечного состояний.

Важнейшими функциями состояния системы являются внутренняя энергия U, энтропия S и свободная энергия F = U – T* 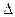S , где T* 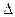S – это часть внутренней энергии, которая не может быть превращена в теплоту и называется связанной энергией.

Изменение энтропии можно подсчитать по следующей формуле:

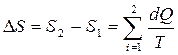(1)

По закону изменения энтропии системы в обратном процессе можно судить о направлении теплообмена (при нагревании тела возрастает, при охлаждении – убывает). При равновесных адиабатических процессах dQ = 0 и S не изменяется. При других процессах – изохорическом, изобарическом и изотермическом энтропии изменяется.

Так для изотермического процесса (Т = const ) :

.

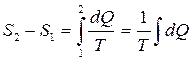В неизолированных системах S всегда возрастает, и уравнение будет иметь вид:

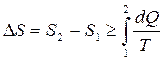
Знак равенства относится к обратимым процессам (т.е. процессам, которые можно провести в обратном направлении через те же самые состояния), а знак неравенства – к необратимым. Все реальные процессы – необратимы.

Между энтропией и вероятностью состояния существует связь. Больцман установил ее в виде соотношения:

S = k*ln*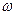

где k – постоянная Больцмана,

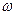- число различных способов, которыми может быть реализовано определенное состояние, называемое термодинамической вероятностью.

В соответствии с формулой Больцмана второе начало термодинамики можно сформулировать следующим образом: «Во всякой изолированной системе происходит такие изменения, которые приводят систему к наиболее вероятному состоянию».

II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.

В данной работе рассматривается изменение энтропии при нагревании и плавлении нафталина. Так как нафталин является кристаллическим веществом, то он плавится при определенной температуре.

Количество теплоты, которое надо затратить, чтобы нагреть нафталин от комнатной температуры Т_к до температуры плавления Т_п определяется по формуле:

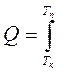С*m*d*T ,

где С – удельная теплоемкость нафталина (1222 Дж/кг*К)

m - масса нафталина.

Количество теплоты, необходимое для плавления нафталина при температуре плавления (Т_п=const), равно:

Q₂ = 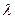*m , где

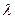- удельная теплота плавления нафталина (2*10⁵ Дж/кг).

Тогда приращение энтропии 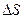при плавлении нафталина можно подсчитать по формуле (1), подставив вместо Q его значение Q₁ + Q₂ . Тогда получим:

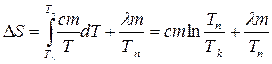(2)

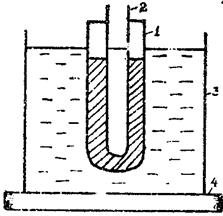
Рис.1

Экспериментальная установка для определения (рис.1) состоит из пробирки нафталином 1, в которую помещен термометр 2. Пробирка опускается в стакан с водой 3, который ставится на электрическую плитку 4.

III. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

1. Соберите установку по схеме (рис. 1)

2. Включите плитку в сеть и следите за изменением температуры в пробирке.

3. Как только температура нафталина станет выше комнатной, снимите показания термометра через каждые 15 секунд до температуры нафталина 95-100⁰С.

4. Выключите плитку из сети и освободите пробирку нафталином от сосуда с водой.

5. Снимите показания термометра через каждые 15 секунд в обратном порядке (при охлаждении нафталина).

6. Результаты измерений занесите в таблицу 1:

Таблица 1

№ п/п	Время нагревания, с	Температура
t, 0С	Т, К

7. Постройте график зависимости температуры нафталина от времени его нагрева и охлаждения и сделайте выводы.

8. Вычислите по формуле (2) приращение энтропии 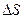при нагревании и плавлении нафталина.

9. Сделайте выводы.