МЕТОДОМ СТОЯЧИХ ЗВУКОВЫХ ВОЛН
Теплоемкость тела характеризуется количеством теплоты,необходимым для нагревание этого тела на один градус (Дж/град). Если для увеличения температуры тела на Т градусов необходимо сообщить ему ΔQ джоулей, то средняя теплоемкость тела в интервале ΔТ определяется как:
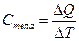 (1)
(1)
Теплоемкость тела пропорциональна массе и зависит от вещества тела. Удельная теплоемкость Суд данного вещества (дерева, железа, воздуха и т. д.) характеризуется количеством тепла на один градус, и измеряется в Дж/кг град. Удельная теплоемкость.
Для газов удобно пользоваться молярной теплоемкостью (Смол или просто С), характеризующейся количеством теплоты, нужным для нагревания одного киломоля данного вещества на один градус.
Очевидно, что
Суд/Дж/кг*град/*μ/кг/кмоль/ = С /Дж/кмоль*град/.
Поскольку в 1 киломоле любого газа содержится одинаковое количество молекул, а средняя кинетическая энергия молекул не зависит от их массы, то можно ожидать, что молярные теплоемкости всех достаточно разреженных газов должны быть одинаковыми.

Теплоемкость тела существенно зависит от того, как меняются состояния тела в процессе нагревания. Рассмотрим для простоты идеальный одноатомный газ. Если мы будем нагревать газ, заключенный в замкнутом объеме, V = const (рис. 1, а), то все подводимое тепло ΔQ будет идти только на увеличение внутренней энергии газа. Тогда первое начало термодинамики при ΔA = 0 будет иметь вид: ΔQ = ΔU.
При этом температура газа будет возрастать в соответствии с увеличением его внутренней энергии, откуда следует, что температура идеального газа пропорциональна его внутренней энергии. Давление газа Р. также будет возрастать пропорционально температуре. Обозначим теплоемкость газа при постоянном объеме через С.
Если хотим, чтобы в процессе нагревания сохранилось давление, газу следует предоставить возможность расширяться. Для этого поместим газ в цилиндр с поршнем, на который действует постоянное давление Р. = const (рис. 1, б). Так как внутренняя энергия U идеального газа не зависит от его объема, то количество теплоты, необходимое для ее увеличения, останется тем же. Но при нагревании газа до той же температуры часть подводимого тепла расходуется теперь на работу против внешних сил при расширении газа. Следовательно, для нагревания газа до той же температуры, как и в предыдущем случае (V = const), придется затратить большее количество теплоты. Таким образом, теплоемкость ΔQ/ΔТ газа при постоянном давлении, которую мы обозначим через Ср., будет больше, чем СV.
Рассмотренный пример очень важен. Он показывает, что количество теплоты ΔQ, необходимое для нагревания газа на ΔТ градусов, существенно зависит от дополнительных условий – характера измерений других микроскопических параметров, определяющих состояние газа, т. е. Р. и V. Кроме рассмотренных процессов, характеризуемых простейшими дополнительными условиями V = const и Р. = const, можно рассмотреть и множество других, отвечающих различным изменениям V и Р. при нагревании. Каждому процессу будет отвечать своя теплоемкость С.
Величины Ср. и Сv для идеального газа оказывается связанными простым соотношением:
Ср. – Сv = R (2)
Это соотношение носит название закона Роберта Майера, полученного им в 1842 году.
Для идеального газа молярная теплоемкость при постоянном давлении превышают молярную теплоемкость при постоянном объеме на величину R т. е. на 8,31 кДж/кмоль град.
Универсальная газовая постоянная R численно равна работе расширения киломоля идеального газа при нагревании его на один градус при постоянном давлении.
Опыт показывает, что во всех случаях превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. Поскольку тепловое движение есть в конечном счете, тоже механическое движение отдельных молекул (только не направленное, а хаотическое), то при всех этих превращениях должен соблюдаться закон сохранения энергии с учетом энергии не только внешних, но и внутренних движений. Такая общая формулировка этого закона носит название первого начала термодинамики и записывается в виде:
ΔQ = ΔU + ΔA, т. е.
Количество теплоты, сообщенное телу (ΔQ), идет на увеличение внутренней энергии (ΔU) и на совершение теплом работы (ΔА).
Однако, если сосуд с расширяющим газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. ΔQ = 0. Процесс, происходящий при таком условии, называется адиабатическим. Уравнение первого начала термодинамики для адиабатического процесса тогда примет вид:
ΔQ = 0 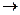 0 = ΔU + ΔA или ΔА = - ΔU. (3)
0 = ΔU + ΔA или ΔА = - ΔU. (3)
Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательная (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают.
Теплоемкость при адиабатическом процессе будет равна 0, т. е.
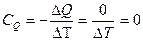
Уравнение, описывающее адиабатический процесс имеет вид:
PVγ = const ; где γ = СР/СV. (4)
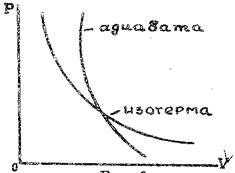
Рис.2
Так как СР>СV, то γ>1 и кривая, изображаемая уравнением (4), идет круче изотермы (рис. 2). Величина работы адиабатического процесса может быть особенно просто вычислена с помощью уравнения (3):

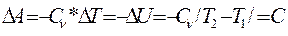
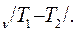
Для одноатомного газа С 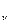 =12,5кДж/к моль град, Ср.=Сv+ =20,8 кДж/к моль град и показатель степени адиабаты γ=СР/Сv=1,67.
=12,5кДж/к моль град, Ср.=Сv+ =20,8 кДж/к моль град и показатель степени адиабаты γ=СР/Сv=1,67.
Для двухатомных газов при обычных температурах
g=29,1/20,8=1,4.
Для многоатомных газов γ еще ближе к единице.
В быстроходных двигателях внутреннего сгорания и при истечении газов через сопла реактивных двигателей процесс расширения газа протекает настолько быстро, что его можно считать практически адиабатическим и
рассчитывать по уравнению /4/.
Опыт также показывает, что для звуковых колебаний с минимальными частотами за время одного колебания /~0,1с/температура между сжатыми/ и тем самым разогретыми/ и разряженными /и тем самым охлажденными/ областями волны не успевает выравниваться. Практически процесс распространения звука можно считать адиабатическим, так что скорость распространения звука в идеальном газе определяется выражением :
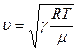 ,
,
где 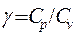
Отсюда легко найти 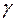 :
:

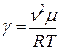 (5)
(5)
Таким образом, определение γ сводится к измерению скорости звука и абсолютной температуры воздуха. В данной работе скорость звука определяется методом стоячих волн - методом Кундта.
II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Схема экспериментальной установки изображена на рисунке 3. Телефон т, получая электрический сигнал от генератора1, излучает звуковые волны в трубу 2. Достигнув микрофона М, звуковая волна преобразуется в напряжение, которое поступает на вертикально отклоняющие пластины У электронного осциллографа 3.Напряжение на горизонтально отклоняющие пластины X подается непосредственно с выходных клемм звукового генератора. Телефон жестко закреплен на левом конце трубы, а микрофон может свободно перемещаться внутри нее.
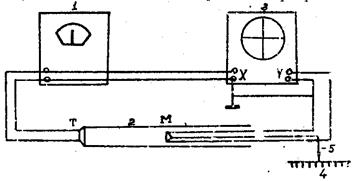
Рис.3
Фазовый сдвиг сигнала, поступающего на пластины У, относительно сигнала, подведенного к пластинам X зависит от времени, которое тратит звук на прохождение расстояния между микрофоном и телефоном, может быть использована для определения длины волны λ. При включении установки на экране осциллографа должен быть виден эллис. Изменяя расстояние между микрофоном и телефоном, можно добиться превращения эллипса в прямую линию. Если теперь сместить микрофон на λ/2, то на экране вновь возникнет прямая линия, проходящая на этот раз через другие квадранты. При дальнейшем смещении прямая вновь переменит свое направление и т.д. Таким образом, при помощи фигур, получивших название фигур Лиссажу, можно непосредственно измерить длину звуковой волны в воздухе и по формуле 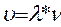 определить скорость звука, где
определить скорость звука, где  - частота генератора в Гц.
- частота генератора в Гц.
III.ПОРЯДОК ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ.
1. Включите осциллограф и дайте ему прогреться в течение 10 минут.
2. Включите и настройте звуковой генератор на частоту 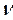 /частота задается преподавателем/.Установите напряжение на выходе генератора 1,5 В.
/частота задается преподавателем/.Установите напряжение на выходе генератора 1,5 В.
3. Установите указатель штока микрофона 5 в крайнее правое положение шкалы 4 /рис/, при этом на экране осциллографа появится фигура Лиссажу /эллипс или прямая линия/.
4. Перемещая шток с микрофоном в лево, зафиксируйте положение штока микрофона / 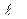 /, при которых эллипс превращается в четкую прямую линию, что соответствует узлам стоячей волны /отсчет производить в см по шкале 4/.
/, при которых эллипс превращается в четкую прямую линию, что соответствует узлам стоячей волны /отсчет производить в см по шкале 4/.
5. Вычислите разность между узловыми точками, которая является половиной длины волны 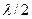 .
.
6. Вычислите длину волны 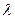 и скорость звуковой волны по формуле
и скорость звуковой волны по формуле 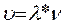 .
.
7. Определите термометром температуру окружающей среды.
8. Вычислите по формуле /5/.
9. Оцените погрешность измерений по формуле :

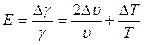 ;
; 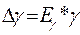

10. Результаты измерений занесите в таблицу :
Таблица 1
Результаты эксперимента
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| Ср. |
11.Сделайте выводы.
Дата добавления: 2015-06-17; просмотров: 1648;
