Теоретическая часть. Механика твердого тела основана на использовании абстрактной модели – понятии «абсолютно твердого тела»
Механика твердого тела основана на использовании абстрактной модели – понятии «абсолютно твердого тела». Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться, т.е. при любых условиях расстояние между какими-либо двумя его точками (или частицами тела) остается постоянным. В природе абсолютно твердых тел нет, т.е. это – идеализированная модель.
Деформацией твердого тела называется изменение его размеров и объема, сопровождающееся чаще всего изменением формы этого тела. Лишь в случаях всестороннего равномерно распределенного по поверхности тела сжатия или растяжения форма тела не меняется.
Причины деформаций:
- изменение температуры (тепловое расширение);
- внешние силовые воздействия.
При деформациях происходят смещения частиц, находящихся в узлах кристаллической решетки, из первоначальных положений в новые, т.е. изменяется взаимное расположение частиц тела. Это приводит к следующему: 1) возникновению упругих сил взаимодействия между частицами (смещенными от положения равновесия), которые стремятся вернуть их в исходные положения; внутренние упругие силы уравновешивают внешние силовые факторы, приложенные к телу; 2) увеличению потенциальной энергии деформируемого тела на величину работы, совершенной при смещении частиц, по преодолению внутренних упругих сил.
Различают упругие и пластические (остаточные) деформации. В первом случае тело полностью, а во втором лишь частично, восстанавливает свои прежние размеры и форму после снятия внешней нагрузки. В реальности все деформации в той или иной степени пластичны. Но если остаточные деформации пренебрежимо малы, то можно считать деформацию упругой. Этому отвечают малые деформации. В пределах малых деформаций все деформации удовлетворяют следующим основным законам:
- в пределах упругости деформация пропорциональна величине внешнего усилия;
- перемена знака внешнего усилия вызывает только перемену знака деформации, без изменения ее абсолютной величины;
- при действии нескольких внешних усилий общая деформация равна сумме частных деформаций.
В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига.
Остановимся на одностороннем или продольном растяжении (сжатии), которое состоит в увеличении (уменьшении) длины тела под действием растягивающей (сжимающей) силы F. Для этого рассмотрим однородный стержень (проволоку) длиной l и площадью поперечного сечения S, один конец которого закреплен, а к другому приложена сила F, изменившая длину стержня на величину Δl . Величина силы 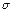 , приходящаяся на единицу площади поперечного сечения стержня, называется напряжением:
, приходящаяся на единицу площади поперечного сечения стержня, называется напряжением:
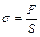 . (13.1)
. (13.1)
Мерой деформации служит относительная деформация, которая в данном случае определяется как относительная продольная деформация:
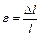 . (13.2)
. (13.2)
Величины 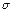 и
и 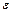 связаны в случае упругих деформаций законом Гука:
связаны в случае упругих деформаций законом Гука:
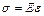 . (13.3)
. (13.3)
Используя соотношения (13.1)-(13.3) получим:
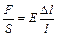 ,
,
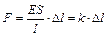 . (13.4)
. (13.4)
Коэффициент пропорциональности Е в формуле (13.3) называется модулем Юнга. Он является характеристикой упругих свойств материала, а коэффициент k в (13.4) называется коэффициентом упругости тела. Из (13.3) и (13.4) следует, что модуль Юнга определяется напряжением, вызывающим удвоение длины стержня. Таким образом, модуль Юнга равен напряжению, при котором относительное удлинение стало бы равным единице, если бы при таком относительном удлинении еще сохранялась пропорциональность между ним и напряжением. В действительности, гораздо раньше, чем будет достигнуто напряжение, равное модулю Юнга, тело начнет испытывать пластическую деформацию, а затем подвергнется разрыву. Деформация твердых тел подчиняется закону Гука лишь до определенного предела ( 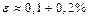 ), называемого пределом пропорциональности. Продольная деформация стержня всегда вызывает его поперечную деформацию: удлиняясь стержень становится соответственно тоньше. Относительная поперечная деформация:
), называемого пределом пропорциональности. Продольная деформация стержня всегда вызывает его поперечную деформацию: удлиняясь стержень становится соответственно тоньше. Относительная поперечная деформация:
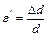 , (13.5)
, (13.5)
где d – диаметр стержня. Из опыта вытекает взаимосвязь:
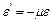 , (13.6)
, (13.6)
где μ – положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона.
Рассчитаем работу, которую нужно совершить, чтобы растянуть данный стержень на величину Δl. Чтобы растягивать стержень, нужно в каждый момент времени действовать на него с силой, соответствующей текущему удлинению и определяемой по формуле (13.4). Таким образом, искомая работа А определяется как:
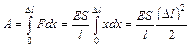 . (13.7)
. (13.7)
С другой стороны, работа равна изменению потенциальной энергии тела: 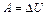 . Принимая за ноль значение потенциальной энергии тела в отсутствие деформации, получим выражение для определения потенциальной энергии
. Принимая за ноль значение потенциальной энергии тела в отсутствие деформации, получим выражение для определения потенциальной энергии 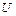 упруго деформированного тела:
упруго деформированного тела: 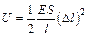 или
или
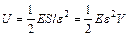 . (13.8)
. (13.8)
где 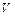 - объем стержня (изменение объема стержня при его деформации здесь не учитывалось).
- объем стержня (изменение объема стержня при его деформации здесь не учитывалось).
Величина, определяемая как
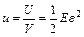 , (13.9)
, (13.9)
называется плотностью потенциальной энергии. В случае однородного стержня при одинаковой в любой его точке деформации энергию можно считать равномерно распределенной по объему стержня. В общем случае неоднородной деформации плотность энергии может меняться от точки к точке.
Выразим модуль Юнга из формулы (13.4):
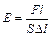 . (13.10)
. (13.10)
В случае исследования проволоки цилиндрической формы площадь ее поперечного сечения равна 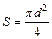 . Тогда расчетная формуладля нахождения значения модуля Юнга материала, из которого изготовлена проволока может быть записана как:
. Тогда расчетная формуладля нахождения значения модуля Юнга материала, из которого изготовлена проволока может быть записана как:
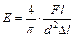 . (13.11)
. (13.11)
Дата добавления: 2015-06-17; просмотров: 628;
