Теоретическая часть. Метод крутильного баллистического маятника, используемый в данной работе для определения скорости пули

Метод крутильного баллистического маятника, используемый в данной работе для определения скорости пули, основан на применении закона сохранения момента импульса и основного уравнения динамики вращательного движения твердого тела. Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением (рис. 11.1):

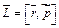
, (11.1)

где 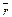− радиус-вектор, проведенный из точки О в точку А, 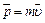−импульс материальной точки А. Модуль вектора момента импульса:

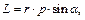(11.2)

где α – угол между векторам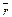и и .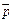

При вращении твердого тела вокруг неподвижной оси Z каждая его частица массой m_i движется по окружности постоянного радиуса r_i с некоторой скоростью υ_i . В этом случае – 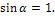Момент импульса отдельной частицы тела равен:

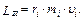(11.3)

Момент импульса твердого тела относительно оси Z есть сумма моментов импульса отдельных частиц тела:

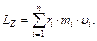(11.4)

Используя соотношение 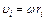, получим:

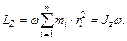(11.5)

Таким образом, момент импульса твердого тела относительно оси Z равен произведению момента инерции тела относительно той же оси на угловую скорость вращения.

Если продифференцировать по времени это выражение, то получим уравнение:

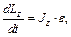(11.6)

где ε – угловое ускорение твердого тела.

Основное уравнение динамики вращательного движения тела относительно неподвижной оси Z имеет вид: 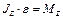, где 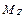момент внешних сил, действующих на тело относительно оси Z. Тогда уравнение (11.6) можно записать: 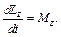Данное уравнение также называется уравнением динамики вращательного движения тела (другая форма записи) и в векторном виде может быть представлено следующим образом:

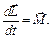(11.7)

В замкнутой системе момент внешних сил равен нулю ( 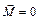), поэтому 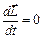, следовательно:

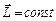. (11.8)

Это выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется со временем.

Используя закон сохранения момента импульса и уравнение динамики вращательного движения, можно изучать взаимодействия тел, в результате которых одно из них начинает вращаться.

Соударение пули с баллистическим крутильным маятником является одним из таких взаимодействий. Крутильный маятник представляет собой симметричное тело, закрепленное вертикально с помощью двух упругих нитей. Ось вращения маятника проходит через точки крепления подвеса и центр масс тела (рис.11.2). Если повернуть тело в горизонтальной плоскости на угол φ, то в закручивающихся нитях подвеса возникают силы, возвращающие его в начальное положение. При небольших углах закручивания момент этих сил относительно оси маятника пропорционален величине угла:

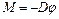, (11.9)

где D – постоянная упругих сил (постоянная кручения).

Когда горизонтально летящая пуля попадает в маятник, то происходит неупругое соударение этих тел. После удара маятник начинает совершать крутильные колебания относительно оси вращения. Движение колебательной системы определяется уравнением гармонических колебаний, которое следует из основного закона динамики вращательного движения (11.7) и соотношения (11.9):

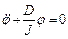. (11.10)

где J – момент инерции колебательной системы относительно оси вращения, .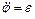

Решением этого уравнения является:

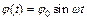, (11.11)

где φ₀ – максимальный угол отклонения маятника, ω – частота колебаний маятника. Согласно закону сохранения момента импульса начальные условия для данной системы имеют вид:

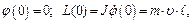(11.12)

где m –масса пули, υ – ее скорость, ℓ – расстояние от оси вращения маятника до точки попадания пули.

Из(11.11)можно определить, что:

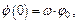(11.13)

где 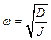циклическая частота колебаний системы (маятника).

Соответственно, период колебаний маятника:

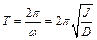. (11.14)

Из (11.12) и (11.13) можно определить скорость пули:

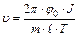. (11.15)

Момент инерции данной колебательной системы (маятника) (рис.11.4) можно рассчитать, используя соотношение:

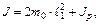(11.16)

где m₀ – масса груза, ℓ₁ = 0,0525 м – расстояние от оси вращения до центров масс грузов, 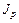– момент инерции свободной рамки (без грузов).

Момент инерции колебательной системы можно найти из отношения квадратов периодов колебаний свободной рамки и колебательной системы. Квадрат периода колебаний свободной рамки определяется следующим образом:

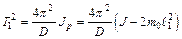(11.17)

Следовательно:

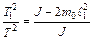. (11.18)

Отношение (11.18) позволяет определить момент инерции колебательной системы:

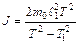. (11.19)

Скорость пули можно найти из (11.15), используя соотношение (11.19):

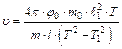. (11.20)