Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. 4 страница
Айналмалы қозғалыстағы дененің М нүктесінің 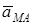 үдеуінің модулі мен бағыты былай табылады
үдеуінің модулі мен бағыты былай табылады
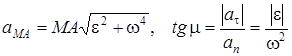 . (6)
. (6)
Ð  –
– 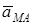 вектордың МА бағытымен құратын бұрышы. Есеп шығару барысында (6)-ды
вектордың МА бағытымен құратын бұрышы. Есеп шығару барысында (6)-ды
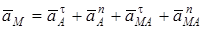 (7)
(7)
түрінде жазған ыңғайлы.
Жанама үдеу 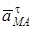 МА кесіндісіне перпендикуляр. Егер қозғалыс үдемелі болса, онда оның бағыты дененің айналу бағытымен бірдей болады; егер дененің қозғалысы кемімелі болса, онда оның бағыты дененің айналуына қарсы бағытта болады.
МА кесіндісіне перпендикуляр. Егер қозғалыс үдемелі болса, онда оның бағыты дененің айналу бағытымен бірдей болады; егер дененің қозғалысы кемімелі болса, онда оның бағыты дененің айналуына қарсы бағытта болады.
Жазық қозғалыстағы дененің кез келген М нүктесінің үдеуін табу үшін, А полюстың 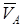 жылдамдығы мен
жылдамдығы мен 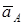 үдеуі немесе полюстың жылдамдығы мен басқа бір нүктенің траекториясы белгілі болуы керек.
үдеуі немесе полюстың жылдамдығы мен басқа бір нүктенің траекториясы белгілі болуы керек.
2.8.2 Лездік үдеулер центрі.
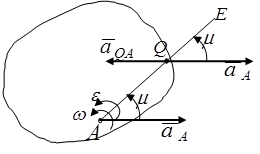 Дененің жазық-параллель қозғалысында оның S қимасында кез келген кезде үдеуі нөлге тең бір Q нүкте болады. Мұндай нүктені лездік үдеулер центрі деп атаймыз.
Дененің жазық-параллель қозғалысында оның S қимасында кез келген кезде үдеуі нөлге тең бір Q нүкте болады. Мұндай нүктені лездік үдеулер центрі деп атаймыз.
Лездік үдеулер центрін табу үшін (S) қимада кез келген бір А нүктенің 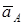 үдеуі мен
үдеуі мен 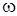 және
және 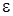 белгілі болуы қажет. Олар белгілі болса,
белгілі болуы қажет. Олар белгілі болса,
1)  бұрышын табамыз:
бұрышын табамыз:
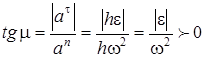 .
.
2) 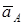 үдеу векторымен
үдеу векторымен  бұрышын құратын АЕ түзуін жүргіземіз. Егер айнала қозғалыс үдемелі болса, үдеу векторынан
бұрышын құратын АЕ түзуін жүргіземіз. Егер айнала қозғалыс үдемелі болса, үдеу векторынан  бұрыш оң бағыт жағына, егер айнала қозғалыс кемімелі болса, теріс бағыт жағына құрылады.
бұрыш оң бағыт жағына, егер айнала қозғалыс кемімелі болса, теріс бағыт жағына құрылады.
3) АЕ бойымен AQ кесіндіні белгілейміз:
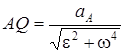 .
.
Q нүктесі лездік үдеу нүктесі болу керек 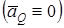 .
.
Енді Q нүктесін полюс деп алсақ, онда кез келген M нүктесі үшін
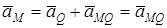 және
және 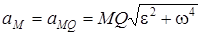 .
.
Соңғы өрнектерден 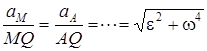 екені анықталады.
екені анықталады.
Нәтижеде
1. кез келген нүктенің үдеуі лездік үдеулер центрін айнала қозғалысының үдеуіне тең.
2. дене нүктелерінің үдеулері сол нүктелерден лездік үдеулер центріне дейінгі қашықтықтарға пропорционал. Лездік жылдамдықтар центрі мен лездік үдеулер центрі үнемі сәйкес келе бермейді.
Негізгі әдебиеттер: 4 [IІ бөлім, 12 тарау, 124-127б], 8 [IІ бөлім, §84].
Қосымша әдебиеттер: 11 [IІ бөлім, 3 тарау, §7, 159-162б].
Бақылау сұрақтары:
1. Жазық фигураның кез келген нүктесінің үдеуін анықтау.
2. 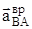 ,
, 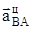 үдеулерінің шамалары мен бағыттары.
үдеулерінің шамалары мен бағыттары.
ДӘРІС-9.Нүктенің күрделі қозғалысы.
2.9.1 Нүктенің салыстырмалы, тасымал және абсолют қозғалыстары.
Егер нүкте екі немесе одан артық қарапайым қозғалыстарға қатысса, онда нүктенің қозғалысын күрделі қозғалыс деп атаймыз.
Мысалы, ұшақтың, кеменің, трамвайдың ішінде кісінің жүруі күрделі қозғалыс болады, өйткені ол, біріншіден, ұшақтың, кеменің, трамвайдың ішінде қозғалады, екіншіден, ұшақпен, кемемен, трамваймен бірге жерге қатысты қозғалады. Судың бетімен келе жатқан қайық та күрделі қозғалыста болады. Ол, біріншіден, суға қатысты қозғалыста, екіншіден, судың жағаға қатысты қозғалысында болады.
Кез келген қозғалыстағы D денені және денеге қатысты, мысалы, оның бетімен қозғалатын, бірақ одан тәуелсіз М нүктені қарастырайық. М нүктеге сәйкес дененің өзінің нүктесін МD деп белгілейік. Oxyz координаттар жүйесін қозғалмалы координаттар жүйесі деп алайық. Қозғалмайтын, мысалы, Жермен байланысқан O1x1y1z1 санақ жүйесін қозғалмайтын координаттар жүйесі дейік.
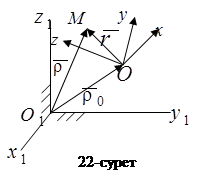 Дененің МD нүктесінің қозғалысын М нүкте үшін тасымал қозғалыс деп атаймыз. Тасымал қозғалыстың сипаттамаларына “е” индексін тіркеп жазамыз:
Дененің МD нүктесінің қозғалысын М нүкте үшін тасымал қозғалыс деп атаймыз. Тасымал қозғалыстың сипаттамаларына “е” индексін тіркеп жазамыз: 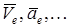 – М нүктесінің тасымал қозғалысының жылдамдығы, үдеуі, т.с.с.
– М нүктесінің тасымал қозғалысының жылдамдығы, үдеуі, т.с.с.
М нүктенің D денеге немесе Oxyz жүйеге қатысты өз қозғалысын оның салыстырмалы қозғалысы дейміз. Салыстырмалы қозғалыстың сипаттамаларына “r” индексін тіркеп жазамыз:
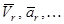 – М нүктесінің салыстырмалы қозғалысының жылдамдығы, үдеуі, т.с.с
– М нүктесінің салыстырмалы қозғалысының жылдамдығы, үдеуі, т.с.с
М нүктенің қозғалмайтын O1x1y1z1 жүйеге қатысты қозғалысын оның абсолют қозғалысы деп атаймыз. Ол тасымал және салыстырмалы қозғалыстардан құралады.
М нүктенің абсолют қозғалысы 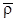 - радиус вектормен, “О” полюстің абсолют қозғалысы
- радиус вектормен, “О” полюстің абсолют қозғалысы 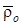 - радиус вектормен, М нүктенің салыстырмалы қозғалысының
- радиус вектормен, М нүктенің салыстырмалы қозғалысының 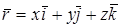 радиус вектормен беріледі (22-сурет).
радиус вектормен беріледі (22-сурет).
Күрделі қозғалыстың негізгі мәселесі абсолют, салыстырмалы, тасымал қозғалыстарының жылдамдықтарының, үдеулерінің арасындағы байланыстарды табу.
2.9.2 Жылдамдықтарды қосу теоремасы.
Нүктенің абсолют қозғалысы тасымал және салыстырмалы қозғалыстардан құралады. Дененің тасымал қозғалысының өзі күрделі қозғалыс. Жалпы жағдайда, МD нүкте “О” полюспен бірге ілгерілемелі және полюсқа қатысты айналма қозғалыста болады.
Нүктенің абсолют қозғалысы
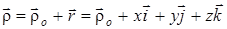 (а)
(а)
теңдеуімен беріледі. Олай болса абсолют жылдамдық
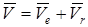 . (1)
. (1)
Теорема. Нүктенің абсолют жылдамдығы оның тасымал және салыстырмалы қозғалыс жылдамдықтарының геометриялық қосындысына тең.
Абсолют жылдамдықтың сан мәні (модулі)
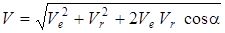 , (2)
, (2)
мұндағы 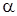 -
- 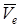 және
және 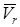 векторларының арасындағы бұрыш.
векторларының арасындағы бұрыш.
Егер тасымал қозғалыс ілгерілемелі болса, онда
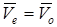 .
.
2.9.3 Үдеулерді қосу теоремасы. (Кориолис теоремасы)
Нүктенің абсолют үдеуін табу үшін абсолют жылдамдықтан уақыт бойынша туынды аламыз. Сонда
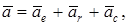 (3)
(3)
мұндағы 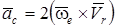 - Кориолис немесе бұру үдеуі деп аталады, яғни нүктенің Кориолис үдеуі тасымал қозғалыстың бұрыштық жылдамдығы мен салыстырмалы жылдамдықтың екі еселенген векторлық көбейтіндісіне тең. Кориолис удеуі векторының бағыты
- Кориолис немесе бұру үдеуі деп аталады, яғни нүктенің Кориолис үдеуі тасымал қозғалыстың бұрыштық жылдамдығы мен салыстырмалы жылдамдықтың екі еселенген векторлық көбейтіндісіне тең. Кориолис удеуі векторының бағыты 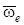 және
және 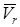 векторлары арқылы өтетін жазықтыққа перпендикуляр.
векторлары арқылы өтетін жазықтыққа перпендикуляр.
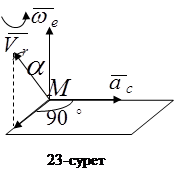 |
Жуковский ережесі: Кориолис удеуі векторының бағытын анықтау үшін салыстырмалы жылдамдық векторын тасымал бұрыштық жылдамдық векторына перпендикуляр жазықтыққа проекциялап, осы проекцияны дененің айналу бағытында  -қа бұру қажет (2-сурет).
-қа бұру қажет (2-сурет).
Кориолис үдеуінің модулі
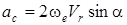 , (4)
, (4)
мұндағы 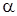 -
- 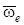 және
және 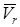 векторларының арасындағы бұрыш.
векторларының арасындағы бұрыш.
Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең.
Абсолют үдеудің сан мәні (модулі)
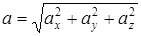 , (5)
, (5)
мұндағы
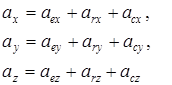
формуласымен анықталады.
Егер тасымал қозғалыс ілгерілемелі қозғалыс болса, 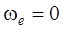 болғандықтан
болғандықтан
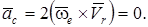
Олай болса,
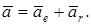 (6)
(6)
Теорема. Егер тасымал қозғалыс ілгерілемелі болса, онда абсолют үдеу тасымал және салыстырмалы үдеулердің геометриялық қосындысына тең.
Бұл жағдайда абсолют үдеудің модулі
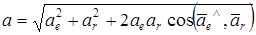 (7)
(7)
Негізгі әдебиеттер: 4 [IІ бөлім, 11 тарау, 101-112б], 8 [IІ бөлім, §§89-91].
Қосымша әдебиеттер: 11 [IІ бөлім, 2 тарау, §7, 144-148б].
Бақылау сұрақтары:
1 Нүктенің абсолют, салыстырмалы және тасымал қозғалыстары.
2 Жылдамдықтарды қосу туралы теорема.
3 Нүктенің тасымал, салыстырмалы, Кориолис және абсолют үдеулері.
4 Үдеулерді қосу туралы Кориолис теоремасы.
5 Кориолис үдеуінің модулін және бағытын анықтау.
6Жуковский ережесі.
Дата добавления: 2015-06-17; просмотров: 4980;
