Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. 1 страница

Дәріс сабақтарының конспектілері

1-модуль «Статика»

ДӘРІС-1.Кіріспе. Статика. Статикаға кіріспе. Жинақталатын күштер жүйесі.

Механиканы теориялық және қолданбалы механика деп екіге жіктейді, бірақ олар бірімен бірі тығыз байланысты. Материялық денелердің қозғалыс заңдарын Теориялық механика ғылымы зерттейді.

Теориялық механика үш бөлімнен тұрады: статика, кинематика, динамика.

1.1.1 Статиканың негізгі ұғымдары. Статика сөзі гректің ‘Status’ деген сөзінен шыққан. Ол тыныштықта болу, бір орында тұру, қозғалмау деген ұғымдарды білдіреді.

Статика – денеге түсірілген күштер жиынын қарапайым түрге келтіретін және олардың тепе-теңдік шарттарын тағайындайтын теориялық механиканың бөлімі. Күш деп денелердің әсерлесуінің өлшеуіші ретінде алынатын шаманы атаймыз. Күш – векторлық шама. Оның денеге әсері модулімен, бағытымен, түсу нүктесімен анықталады.

Күштің өлшем бірлігі халықаралық СИ өлшем бірліктер жүйесінде 1Н (Ньютон), техникалық өлшем бірліктер жүйесінде 1 кг (килограмм күшпен) арқылы анықталады.

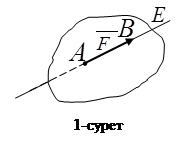Күшті бағытталған 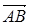кесіндімен бейнелеуге болады (1-сурет). 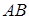кесіндісі 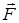күшінің сан мәнін, бағытын, әсер ету нүктесін сипаттайды. Бойымен күш векторы бағытталған DE түзуін күштің әсер ету сызығы деп атаймыз. А нүктесі күштің әсер ету нүктесі болады.

Денеге түскен бірнеше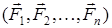

күштердің жиынтығы күштер жүйесі деп аталады. Егер денеге түскен 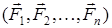бір күштер жүйесін екінші күштер жүйесімен 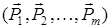алмастырғанда дененің бастапқы күйі өзгермесе, мұндай екі жүйе өзара пара-пар болады

~ .

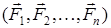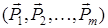Егер күштер жүйесінің әсерінен дене тыныштығы бұзылмаса, мұндай күштер жүйесі нөлге пара-пар болады.

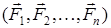~ 0.

Егер денеге түскен 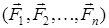күштер жүйесі бір күшке 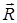пара-пар болса, онда ол күшті тең әсерлі күш деп атайды

~ .

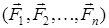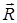Модулі тең әсерлі күшке тең, ал бағыты оның әсер ету сызығы бойымен қарама-қарсы бағытталған күшті теңгеруші күш деп атайды.

1.1.2 Статиканың аксиомалары. Статиканың барлық теоремалары мен теңдеулері аксиомалардың көмегімен қорытып шығарылады.

1-аксиома. Екі күш әсер ететін қатты дене тепе-теңдікте болуы үшін, ол күштердің модульдері тең, ал бағыттары бір түзудін бойымен қарама-қарсы болуы қажетті және жеткілікті.

2-аксиома. Қатты денеге әсер ететін кез келген күштер жүйесіне нөлге пара-пар күштер жүйесін қосқаннан немесе алғаннан бастапқы күштер жүйесінің әсері өзгермейді.

1, 2-аксиомалардың салдары.Әсер ету сызығы бойымен күшті кез келген басқа нүктеге көшіруге болады, одан күштің денеге әсері өзгермейді.

3-аксиома.Қатты дененің бір нүктесіне түскен екі күшті осы

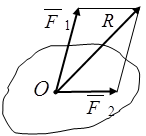күштердің геометриялық қосындысына тең және сол нүктеге түскен тең әсерлі күшпен ауыстыруға болады. Тең әсерлі күш бастапқы күштерден құрылған параллелограммның диагоналімен анықталады.

4-аксиома.Екі дене бір-бірімен сан мәндері тең, бір түзудің бойымен қарама-қарсы бағытталған күштермен әсерлеседі.

5-аксиома.Кез келген механикалық жүйеге қосымша байланыстар қосылса, одан механикалық жүйенің бастапқы тепе-теңдік күйі өзгермейді.

1.1.3 Байланыстар және олардың реакциялары. Егер дененің қозғалысы басқа ешбір денемен шектелмесе, онда мұндай дене еркін дене деп аталады, басқаша жағдайда дене еркін емес дене болады. Қозғалысқа кедергі жасайтын денелерді байланыстардеп атайды. Байланыс тарапынан туатын күш байланыс реакциясы немесе кері әсер күші деп аталады.

Реакциялар денелерді қозғалтпайды, тек қозғалуына кедергі жасайды. Сол себептен реакция күші пассив күштерге жатады. Берілген күштер кейде актив күштер деп аталады. Актив күштер байланыс реакцияларына тәуелсіз. Байланыс реакциялары берілген күштерге тәуелді болады.

Кейбір жиі кездесетін байланыстарды қарастырайық (2-сурет):

а) Жылтыр бет. Мұндай байланыстың реакциясы жанасушы беттерге ортақ нормаль бойымен бағытталады.

б) Егер жанасушы беттердің бірі нүкте болса, онда реакция күші келесі бетке нормаль бойымен бағытталады.

в) Жіп. Жіп АВ бағытында дененің А нүктесінен алыстауына кедергі жасайды. Сол себептен 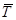реакція күші осы бағытқа қарама-қарсы болып, әр уақытта А – жіптің іліну нүктесіне қарай бағытталады.

г) Жылжымалы цилиндрлік топса. Байланыс өзінің жылжу бағытында топса қозғалысына кедергі жасамайды, оның перпендикуляр бағыттағы жылжуын шектейді. Сол себептен реакция тіреу жазықтығына перпендикуляр бағытталады.

д) Жылжымайтын цилиндрлік топса.Дене цилиндрлік ось бойымен жылжи алады, ал оске нормаль бойымен кез-келген бағытта жылжи алмайды, демек реакция күші оске нормаль жазықтықта жатады, бірақ бағыты белгісіз. Мұнда реакция күші х, у остерінің бағытында құраушы күштерге жіктеледі.

е) Жылжымайтын сфералық топса. Мұндай топсамен байланысқанда дененің бір нүктесі ғана қозғалмайды, бірақ дене сол нүктені айнала алады. Сол себептен байланыс реакциясы кеңістікте кез келген бағытта болуы мүмкін.

Аксиома 6(байланыстар аксиомасы). Денеге әсер ететін байланыстарды алып тастап, олардың әсерін реакцияларымен алмастыру арқылы кез келген еркін емес денені еркін деп қарастыруға болады.

1.1.4 Жинақталатын күштер жүйесі. Әсер ету сызықтары бір нүктеде қиылысатын күштер жинақталатын күштер жүйесі деп аталады.

Жинақталатын күштер жүйесінің тең әсерлі күші. Теорема.Жинақталатын күштер жүйесін осы күштердің геометриялық қосындысына тең және олардың әсер ету сызықтарының қиылысу нүктесіне түсірілген тең әсерлі күшпен алмастыруға болады:

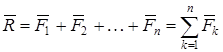, (1)

Жинақталатын күштер жүйесінің тең әсерлі күшін күштер көпбұрышының әдісімен де анықтауға болады. (Көпбұрышты тұрғызу мысалы дәріс оқығанда қарастырылады).

Жинақталатын күштер жүйесінің тең әсерлі күшін күштің координата остеріне проекциялары арқылы аналитикалық түрде анықтауға болады. Бұл жерде векторлардың геометриялық қосындысының кез келген оске проекциясы қосылғыш векторлардың осы остерге проекцияларының қосындысына тең екенін ескереміз. Осыған сәйкес, жинақталатын күштер жүйесін құратын күштердің декарт координата остеріне проекцияларын біле отырып тең әсерлі күштің осы остерге проекцияларын анықтауға болады

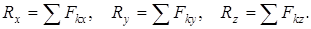(2)

Сонда тең әсерлі күштің модулі

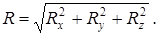(3)

Оның бағыты бағыттаушы косинустармен анықталады

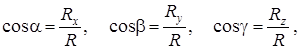(4)

мұндағы 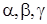– 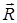векторының 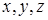өстерімен жасайтын бұрыштары.

Жинақталатын күштер жүйесінің тепе-теңдік шарттары.

Теорема:Жинақталатын күштер жүйесі тепе-теңдікте болу үшін оның тең әсерлі күші (немесе барлық күштердің геометриялық қосындысы) нөлге тең болуы қажетті және жеткілікті:

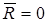. (5)

Геометриялық тұрғыдан бұл осы күштерден тұрғызылған көпбұрыштың тұйық болатынын білдіреді.

Кеңістіктегі жинақталатын күштер жүйесінің қажетті және жеткілікті тепе-теңдік шарттары былай жазылады:

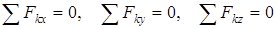. (6)

Теңдеулерге берілген күштермен қатар дененің қозғалыс еркіндігін шектейтін байланыстардың реакциялары да кіреді.

Сонымен, қатты денеге әсер ететін кеңістіктегі жинақталатын күштер жүйесітепе-теңдікте болуы үшін бұл күштердің декарт координата остерінің әрқайсысына проекцияларының қосындысы нөлге тең болуы қажетті және жеткілікті

Сонда, қатты денеге әсер ететін жазықтықтағы жинақталатын күштер жүйесітепе-теңдікте болуы үшін бұл күштердің декарт координата остерінің әрқайсысына проекцияларының қосындысы нөлге тең болуы қажетті және жеткілікті:

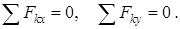(7)

Үш күш туралы теорема. Егер бір жазықтықта жатқан, өзара параллель емес үш күштің әсерінен дене тепе-теңдікте болса, онда күштердің әсер ету сызықтары бір нүктеде қиылысады.

Негізгі әдебиеттер: 4 [I бөлім, 1,2 тараулар, 5-23б], 8 [I бөлім, 1 тарау,9-31б].

Қосымша әдебиеттер: 11 [I бөлім, 1тарау, §§1-4, 5-24б].

Бақылау сұрақтары:

1. Теориялық механика нені зерттейді.

2. Статика нені зерттейді.

3. Күш, күштер жүйесі, пара-пар жүйелер, тең әсерлі күш, теңестірілген күштер жүйесі ұғымдары.

4. Статиканың аксиомалары.

5. Байланыстар және олардың реакциялары.

6. Жинақталатын күштер жүйесі және оның тең әсерлі күші.

7. Жинақталатын күштер жүйесінің тепе-теңдік шарттары.

8.Параллель емес үш күш туралы теорема.

ДӘРІС-2.Моменттер теориясы. Статиканың негізгі теоремасы.

1. Күштің нүктеге қатысты моменті. Күштің әсерінен қатты дене ілгерілемелі немесе айналмалы қозғалыс жасайды. Күштің айналдырушы әсері моментпен сипатталады.

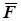күшінің О нүктесіне қатысты моменті деп осы нүктеге түсірілген 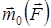векторын айтады. Бұл вектордың модулі (шамасы) күш модулі мен күштің нүктеге қатысты иінінің көбейтіндісіне тең, ал бағыты күш пен нүкте арқылы өтетін күш жазықтығына перпендикуляр, оның ұшынан қарағанда күш денені сағат тіліне қарсы бағытта айналдыратындай болып көрінеді (3-сурет).

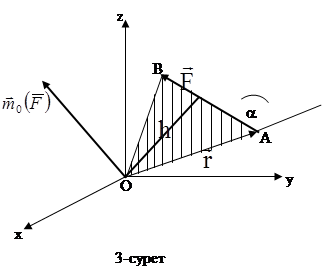Күштің О нүктесіне қатысты моментінің шамасы немесе модулі:

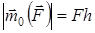. (1)

Күштің нүктеге қатысты иіні (h) деп нүктеден күштің әсер ету сызығына дейінгі ең жақын ара қашықтықты (перпендикулярды) айтады.

Күштің О нүктесіне қатысты моментінің векторын күштің түсу нүктесінің радиус-векторы мен күш векторының векторлық көбейтіндісі ретінде жазуға болады:

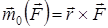. (2)

1. 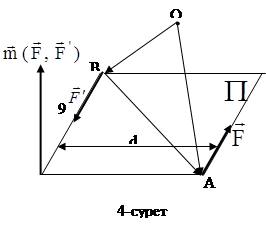Қос күш және оның моменті. Қатты денеге түскен модульдері тең, өзара параллель, бағыттары қарама қарсы кез келген 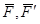күштерді қос күш

деп айтамыз. Қос күштің әсерінен дене айналмалы қозғалыс жасайды, демек, қос күштің моменті болады. Қос күш жатқан 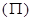жазықтығы қос күштің әсер ету жазықтығы деп аталады. Қос күшті құрайтын күштердің әсер ету сызықтарының арасындағы ең жақын ара қашықтық (перпендикуляр) қос күштің иіні (d) деп аталады (4-сурет).

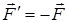екенін ескеріп, кез келген О нүктеге қатысты бұл екі күштің моменттерінің геометриялық қосындысын алуға болады:

.

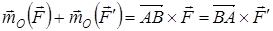Бұл өрнек қос күш моментінің векторы деп аталады, ол О нүктесіне тәуелсіз:

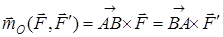. (3)

Қос күш моментінің шамасы (модулі) оны құрайтын күштердің біреуінің модулі мен қос күш иінінің d көбейтіндісіне тең:

.

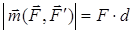Қос күш моменті векторының бағытықос күштің әсер ету жазықтығына перпендикуляр, ұшынан қарағанда қос күш денені сағат тіліне қарсы бағытта айналдыратындай болып көрінеді. Оны кез келген нүктеге түсіруге болады, себебі ол О нүктесіне тәуелсіз, яғни қос күш моментінің векторы – жылжымалы вектор.

1. Қос күштер туралы теоремалар (дәлелдеусіз). 1-теорема. Бір жазықтықта жатқан екі қос күшті моменті осы қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады.

Салдар. Бір жазықтықта жатқан кез келген қос күштер жүйесін моменті барлық қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады.

2-теорема. Моменттері тең екі қос күш өзара пара-пар болады.

1-салдар.Дененің күйін өзгертпейқос күшті параллель жазықтыққа көшіруге болады.

2-салдар.Қос күштің моменті мен айналу бағытын сақтай отырып, оның шамасы мен иінін өзгертуге болады. Одан дененің бастапқы күйі өзгермейді.

3-теорема.Қиылысатын жазықтықтарда жатқанекі қос күшті осы қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады.

1, 2, 3 теоремалардың салдары.Түрлі жазықтықтарда жатқан қос күштердің кез келген санын моменті барлық қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады. Сонымен, денеге әсер ететін қос күштер жүйесі бір қос күшке пара-пар екен. Тең әсерлі қос күштің 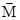моменті құраушы қос күштердің 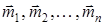моменттерінің геометриялық қосындысына тең:

.

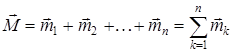Қос күштер жүйесінің тепе-теңдік шарты. Моменттері 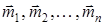қос күштердің әсеріндегі дене тепе-теңдікте болу үшін барлық қос күштердің моменттерінің геометриялық қосындысының нөлге тең болуы қажет және жеткілікті:

.

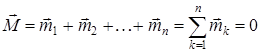1. Күшті параллель көшіру туралы лемма.

Лемма.Дененің бірнүктесіне түскен күшті басқа нүктеге параллель көшіруге болады. Күштің денеге әсері өзгермеу үшін көшірілген күшке моменті

берілген күштің жаңа нүктеге қатысты моментіне тең қос күш қосу керек.

1. Статиканың негізгі теоремасы. Денеге 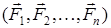күштер жүйесі әсер етсін. Берілген күштердің геометриялық қосындысы жүйенің бас векторы деп аталады:

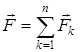. (4)

Барлық күштердің О нүктесіне қатысты моменттерінің геометриялық қосындысы жүйенің О нүктесіне қатысты бас моменті деп аталады:

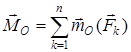.(5)

Теорема. Абсолют қатты денеге әсер ететін кез келген күштер жүйесін берілген О центріне келтіргенде жүйенің бас векторына тең, келтіру центріне түскен бір күшпен және моменті жүйенің бас моментіне тең бір қос күшпен алмастыруға болады.

1. Тепе-теңдік шарттары. Теорема. Кез келген күштер жүйесі тепе-теңдікте болу үшін оның бас векторы мен бас моментінің нөлге тең болуы қажет және жеткілікті (дәлелдеусіз)

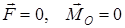. (6)

1. Вариньон теоремасы. Теорема.Жинақталатын күштер жүйесінің тең әсерлікүшінің кез келген нүктеге қатысты моменті жүйе күштерінің сол нүктеге қатысты моменттерінің геометриялық қосындысына тең (дәлелдеусіз)

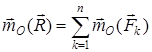. (7)

Негізгі әдебиеттер: 4 [I бөлім, 3-5 тараулар, 24-38б], 8 [I бөлім, §§ 8-13, 31-41б].

Қосымша әдебиеттер: 11 [I бөлім, 2тарау, §§1,2, 24-27б].

Бақылау сұрақтары:

Нүктеге (центрге) қатысты күш моментінің векторы.

Нүктеге қатысты күш иінінің анықтамасы.

Қос күштің, оның иіні мен әсер ету жазықтығының және моментінің анықтамалары.

Қос күш туралы теоремалар.

Қос күштер жүйесінің тепе-теңдік шарттары.

Күшті параллель көшіру туралы лемма.

Статиканың негізгі теоремасы.

Күштер жүйесінің геометриялық тепе-теңдік шарттары.

Вариньон теоремасы.

ДӘРІС-3.Кез келген жазық күштер жүйесі.

1.Әсер ету сызықтары бір жазықтықта кез келген бағытта орналасқан күштер жүйесі жазықтықтағы кез келген күштер жүйесі деп аталады. Мұндай күштердің жазықтықтағы кез келген нүктеге қатысты моменттерінің векторлары осы жазықтыққа перпендикуляр, бір біріне параллель бағытталады. Бұл моменттерді бір бірінен таңбасымен айыруға болады. Осыған байланысты, жазықтықтағы кез келген күштер жүйесі үшін момент векторларының орнына олардың алгебралық шамалары қарастырылады.

1.3.1. Күштің нүктеге қатысты моментінің және қос күш моментінің алгебралық шамалары. Күштің нүктеге қатысты алгебралық моменті депсәйкес таңбамен алынған күш модулі мен күштің нүктеге қатысты иінінің

көбейтіндісін айтады:

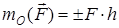. (1)

Егер күш денені сағат тіліне қарсы бағытта бұруға тырысса плюс таңбасы алынады, сағат тілімен бағыттас бұруға тырысса минус таңбасы алынады.

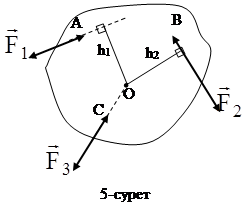Егер күштің әсер ету сызығы нүктеден өтсе, онда оның бұл нүктеге қатысты моменті нөлге тең болады (5- сурет):

, , .

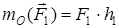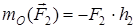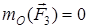Қос күштің алгебралық моменті депплюс немесе минус таңбасымен алынған оны құрайтын күштердің біреуінің модулі мен қос күштің иінінің көбейтіндісін айтады:

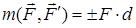. (2)

Егер қос күш денені сағат тіліне қарсы бағытта бұруға тырысса, плюс таңбасы алынады, ал сағат тілімен бағыттас бұруға тырысса, минус таңбасы алынады (6а, 6ә-суреттер)

, .

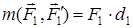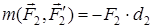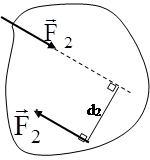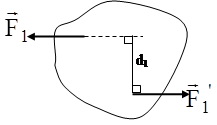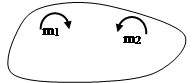а) ә) б)

6-сурет

Қос күштің моменті қос күштің әсерін толық сипаттайтындықтан, кейде қос күшті оның моментінің бағытын көрсететін доғамен бейнелейді 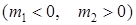(6б-сурет).

1.3.2. Жазықтықтағы кез келген күштер жүйесінің бас векторы мен бас моменті. Жазықтықтағы кез келген күштер жүйесі үшін бас вектор барлық күштердің геометриялық қосындысы болады және декарт координата жүйесінің остеріне проекцияланады: