Күштің кез келген М0М1 орын ауыстырудағы жұмысы элементар жұмыстан осы орын ауыстыру бойымен алынған интегралға тең.
(11) – (14) өрнектеріне сәйкес күш жұмысын төрт түрде жазуға болады:
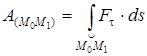 , (15)
, (15)
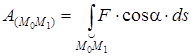 (16)
(16)
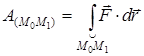 (17)
(17)
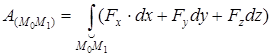 . (18)
. (18)
Барлық жағдайларда интеграл М0М1 қисығы бойымен алынады, яғни қисық сызықты интеграл болады.
Уақыт бірлігі аралығында орындалатын күштің жұмысын анықтайтын шаманы қуат деп атайды. Егер жұмыс бірқалыпты орындалса, қуат
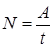 ,
,
мұндағы t – жұмыс жасалатын уақыт. Жалпы жағдайда
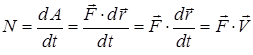 , (19)
, (19)
демек, күш қуаты 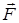 күші мен нүкте жылдамдығының
күші мен нүкте жылдамдығының 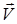 скалярлық көбейтіндісіне тең.
скалярлық көбейтіндісіне тең.
3.12.2 Жұмысты есептеу мысалдары.
· Ауырлық күшінің жұмысы.Ауырлық күші 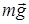 әсер ететін нүкте бастапқы М0 (x0, y0, z0) орнынан М1 (x1, y1, z1)-ге орын ауыстырсын. Ауырлық күшінің жұмысын (18) өрнегімен есептейік, сонда
әсер ететін нүкте бастапқы М0 (x0, y0, z0) орнынан М1 (x1, y1, z1)-ге орын ауыстырсын. Ауырлық күшінің жұмысын (18) өрнегімен есептейік, сонда
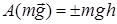 , (20)
, (20)
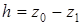 - нүктенің орын ауыстыру биіктігі.
- нүктенің орын ауыстыру биіктігі.
Демек, ауырлық күшінің жұмысы плюс не минус таңбасымен алынған ауырлық күші модулі мен вертикаль орын ауыстырудың көбейтіндісіне тең екен. Плюс таңбасы нүкте төмен орын ауыстырғанда, ал минус таңбасы нүкте жоғары қарай орын ауыстырғанда алынады.
·  Серпімділік күшінің жұмысы. Серіппенің бос ұшына бекітілген және горизонталь жазықтықта жатқан М жүгін қарастырайық (25 сурет). Координатаның О бас нүктесі етіп созылмаған серіппенің ұшын аламыз (
Серпімділік күшінің жұмысы. Серіппенің бос ұшына бекітілген және горизонталь жазықтықта жатқан М жүгін қарастырайық (25 сурет). Координатаның О бас нүктесі етіп созылмаған серіппенің ұшын аламыз ( 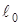 –деформацияланбаған серіппенің ұзындығы). Егер жүкті О тепе-теңдік орнынан серіппенің ұзындығы
–деформацияланбаған серіппенің ұзындығы). Егер жүкті О тепе-теңдік орнынан серіппенің ұзындығы  болатындай етіп созсақ, серіппе
болатындай етіп созсақ, серіппе 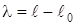 -ге созылады да, жүкке О нүктесіне бағытталған серпімділік күші
-ге созылады да, жүкке О нүктесіне бағытталған серпімділік күші 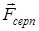 әсер етеді. 25-суреттен
әсер етеді. 25-суреттен  екенін көреміз, сондықтан серпімділік күшін былай жазуға болады:
екенін көреміз, сондықтан серпімділік күшін былай жазуға болады:
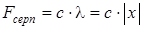 и
и  ,
,
мұндағы с – серіппенің серпімділік коэффициенті.
Жүк бастапқы М0(х0) орнынан М1(х1)-ге орын ауыстырғандағы серпімділік күшінің жұмысын, 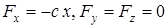 деп алып, (18) теңдеуінен анықтаймыз, демек
деп алып, (18) теңдеуінен анықтаймыз, демек
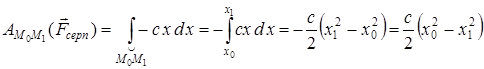 .
.
Бұл өрнектегі х0 серіппенің бастапқы деформациясы l0, ал х1 – соңғы деформациюсы l1. Сондықтан серпімділік күшінің жұмысын мына түрде жазуға болады:
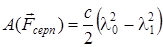 . (21)
. (21)
Демек, серпімділік күшінің жұмысы серіппенің серпімділік коэффициенті мен бастапқы және соңғы деформациялар квадраттары айырмасының көбейтіндісінің жартысына тең.
(21) өрнегі М нүктесінің орын ауыстыруы түзу сызықты болмаса да орын алады. Бұлсерпімділік күшінің жұмысы нүкте траекториясының түріне тәуелді емес екендігін көрсетеді.
· Үйкеліс күшінің жұмысы. Егер нүкте кедір-бұдырлы жазықтықпен қозғалса, оған әсер ететін үйкеліс күшінің модулі f N болады. Бұл жерде f – үйкеліс коэффициенті, ал N – жазықтықтың нормаль реакциясы. Үйкеліс күші қозғалысқа қарсы бағытталғандықтан 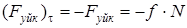 және (15) өрнегі бойынша
және (15) өрнегі бойынша
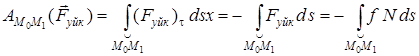 . (22)
. (22)
Егер үйкеліс күші тұрақты болса, онда
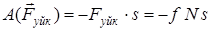 , (23)
, (23)
s – нүкте қозғалатын М0М1 қисығы доғасының ұзындығы.
Сонымен, сырғанау үйкелісі күшінің жұмысы әрқашан теріс таңбалы және нүктенің жүріп өткен жолына тәуелді екен.
3.12.3 Нүктенің кинетикалық энергиясы және оның өзгеруі туралы теорема. Нүкте қозғалысының келесі динамикалық сипаттамасы – кинетикалық энергия.
Нүктенің кинетикалық энергиясы деп оның массасы мен жылдамдығының квадратының көбейтіндісінің жартысына тең 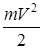 скаляр шаманы айтады.
скаляр шаманы айтады.
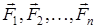 күштер әсер ететін М материялық нүктені қарастырайық. Ол қисық бойымен
күштер әсер ететін М материялық нүктені қарастырайық. Ол қисық бойымен 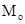 орыннан
орыннан 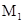 орынға орын ауыстырсын.
орынға орын ауыстырсын.  сәйкесінше
сәйкесінше 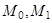 нүктелердегі жылдамдықтары болсын.
нүктелердегі жылдамдықтары болсын.
Нүкте динамикасының негізгі теңдеуінен (Ньютонның екінші заңы):
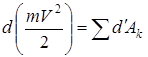 . (24)
. (24)
(24) – нүктенің кинетикалық энергиясының өзгеруі туралы теореманың дифференциалдық түрі деп аталады:нүктенің кинетикалық энергиясының толық дифференциалы нүктеге әсер ететін барлық күштердің элементар жұмыстарының қосындысына тең.
Бұл теоремадан
 (25)
(25)
екенін көреміз, яғни нүктенің кинетикалық энергиясының толық дифференциалы нүктеге әсер ететін барлық күштердің қуаттарының қосындысына тең.
Нүкте бастапқы М0 орыннан М1-ге орын ауыстырғанда оның бастапқы жылдамдығы 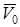 -ден
-ден 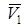 -ге дейін өзгеретінін ескеріп, (24) теңдеуін интегралдаймыз, сонда:
-ге дейін өзгеретінін ескеріп, (24) теңдеуін интегралдаймыз, сонда:
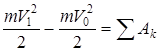 . (26)
. (26)
(26) – нүктенің кинетикалық энергиясының өзгеруі туралы теореманың интералдық (шекті) түрін береді:нүкте шекті орын ауыстырғандағы оның кинетикалық энергиясының өзгеруіосы орын ауыстыруда нүктеге әсер ететін барлық күштердің жұмыстарының алгебралық қосындысына тең.
3.12.4 Материялық нүкте үшін Даламбер принципі.Материялық нүкте үшін Даламбер принципі нүкте динамикасының есептерін статиканың қарапайым әдістерімен шығаруға мүмкіндік береді.
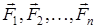 актив күштері мен
актив күштері мен 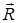 реакция күші әсер ететін материялық нүктені қарастырайық. Бұл нүкте үшін динамиканың негізгі заңы
реакция күші әсер ететін материялық нүктені қарастырайық. Бұл нүкте үшін динамиканың негізгі заңы
 . (27)
. (27)
түрінде жазылады. Соңғы өрнекті түрлендірейік:
 . (28)
. (28)
Белгілеу енгізейік:
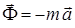 . (29)
. (29)
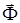 векторы материялық нүктеніңинерция күші деп аталады. Оның модулі нүктенің массасы мен үдеуінің көбейтіндісіне тең, ал бағыты үдеу векторына қарама-қарсы болады.
векторы материялық нүктеніңинерция күші деп аталады. Оның модулі нүктенің массасы мен үдеуінің көбейтіндісіне тең, ал бағыты үдеу векторына қарама-қарсы болады.
(29) өрнегін ескерсек (28) теңдеуі мына түрге келеді:
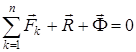 . (30)
. (30)
(30) – материялық нүкте үшін Даламбер принципі деп аталады:қозғалыстағы материялық нүктеге әсер ететін актив күштер, реакция күші мен инерция күші теңестірілген күштер жүйесін құрайды. Бірақ материялық нүктеге тек актив күштер мен реакция күші ғана әсер ететін ескеру керек, ал инерция күші нүктеге әсер етпейді, сондықтан да ол жасанды күш болады.
Негізгі әдебиеттер: 4 [IІІ бөлім, 15,16 тараулар, 147, 150-152б], 8 [IІІ бөлім, §§112-114].
Қосымша әдебиеттер: 11 [IІІ бөлім, 4 тарау, §§5,6, 323-338б].
Бақылау сұрақтары:
1. Күштің элементар жұмысы; оның аналитикалық өрнегі.
2. Ауырлық күшінің, серпіділік күшінің, тартылу күшінің жұмысы.
3. Нүктенің кинетикалық энергиясының өрнегі.
4. Нүктенің кинетикалық энергиясының өзгеруі туралы теореманың дифференциалдық және интегралдық түрлері.
5. Материялық нүкте үшін Даламбер принципі.
1. Инерция күштері.
ДӘРІС-13.Жүйе динамикасына кіріспе. Инерция моменттері.
«Динамика» бөлімінің бірінші бөлігінде күштер әсеріндегі материялық нүкте қозғалысының заңдарын талдадық. Енді материялық нүктелердің механикалық жүйесінің қозғалысын қарастырайық.
1. Механикалық жүйе, оның массасы мен массалар центрі. Механикалық жүйе деп қозғалыстары мен орны өзара тәуелді болып келетін материялық нүктелер жиынтығын айтады. Қатты дене өзгермейтін механикалық жүйе болып табылады.
Жүйедегі нүктелердің массаларының қосындысына тең шама жүйе массасы деп аталады:
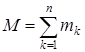 , (1)
, (1)
мұндағы mk – k-номерлі материялық нүктенің массасы, ал n – жүйедегі нүктелердің саны.
Механикалық жүйенің массалар центрі немесе инерция центрі деп радиус-векторы
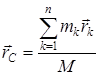 . (2)
. (2)
теңдеуімен анықталатын геометриялық нүктені айтады.
1. Күштердің классификациясы. Статика бөлімі мен нүкте динамикасындағыдай, жүйеге әсер ететін күштерді байланыстарға тәуелсіз актив күштерге және реакция күштеріне бөлуге болады.
Сонымен қатар механикалық жүйеде күштерді сыртқы және ішкі күштер деп те бөледі.
Жүйеге кірмейтін денелердің жүйе нүктелеріне әсерінен туатын күштер сыртқы күштер деп аталады. Бұл күштерді  деп белгілейміз. Жүйе нүктелерінің өзара әсерінен туатын күштер ішкі күштер деп аталады да,
деп белгілейміз. Жүйе нүктелерінің өзара әсерінен туатын күштер ішкі күштер деп аталады да, 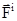 деп белгіленеді.
деп белгіленеді.
Жүйенің ішкі күштерінің екі қасиеті бар:
1. Барлық ішкі күштердің геометриялық қосындысы нөлге тең:
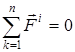 . (3)
. (3)
2. Жүйенің барлық ішкі күштерінің кез келген центрге қатысты моменттерінің геометриялық қосындысы нөлге тең:
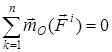 . (4)
. (4)
1. Инерция моменттері.Механикалық жүйенің қозғалысы оның массасына, әсер ететін күштерге және жүйедегі массалардың таралуына тәуелді. Жүйедегі массалардың таралуы оның массалар центрінің орнымен және инерция моментімен сипатталады.
Өске қатысты инерция моменті (өстік инерция моменті). Дененің массасы ілгерілемелі қозғалыста қандай роль атқарса, өстік инерция моменті дененің айналмалы қозғалысында сондай роль атқарады.
Механикалық жүйенің  өсіне қатысты инерция моменті деп жүйенің барлық нүктелерінің массаларының олардан осы өске дейінгі ара қашықтық квадраттарының көбейтіндісіне тең скаляр шаманы айтады:
өсіне қатысты инерция моменті деп жүйенің барлық нүктелерінің массаларының олардан осы өске дейінгі ара қашықтық квадраттарының көбейтіндісіне тең скаляр шаманы айтады:
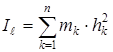 , (5)
, (5)
мұндағы hk – k номерлі нүктенің  өсіне дейінгі ара қашықтығы.
өсіне дейінгі ара қашықтығы.
Механикалық жүйенің x, y және z координата өстеріне қатысты инерция моменттері былай өрнектеледі:
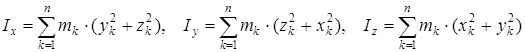 . (6)
. (6)
(5) және (6) өрнектері жүйе үшін де, қатты дене үшін де орын алады. Біртұтас дене жағдайында оны массасы 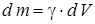 (мұндағы g – дененің тығыздығы),
(мұндағы g – дененің тығыздығы),  элементар көлемдерге бөледі. (5) мен (6) өрнектерінің оң жағындағы суммалар үш еселік интегралға айналады:
элементар көлемдерге бөледі. (5) мен (6) өрнектерінің оң жағындағы суммалар үш еселік интегралға айналады:
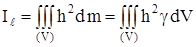 , (7)
, (7)
және
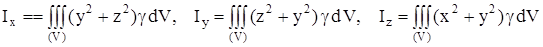 . (8)
. (8)
Бұл өрнектердегі интеграл дененің бүкіл V көлеміне таралады. Кейде оны екі еселік интегралмен немесе анықталған интегралмен алмастыруға болады. Біртекті денелердің инерция моменттерін санағанда олардың g тығыздығы тұрақты шама екенін есте сақтау керек.
Инерция радиусы. Есептеулерде инерция радиусы ұғымы жиі қолданылады. Дененің өске қатысты инерция радиусы деп өстен бүкіл дененің М массасы шоғырланған нүктеге дейінгі r ара қашықтықты айтады. Нүктенің осы өске қатысты инерция моменті дененің сол өске қатысты 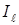 инерция моментіне тең болуы керек:
инерция моментіне тең болуы керек:
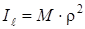 . (9)
. (9)
Инерция радиусын біле отырып, (9) өрнегінен дененің инерция моментін анықтауға болады, немесе керісінше, дененің инерция моментін біле отырып, инерция радиусын анықтауға болады.
Гюйгенс-Штейнер теоремасы. Біреуі массалар центрі арқылы өтетін өзара параллель өстерге қатысты дененің инерция моменттерінің арасындағы тәуелділікті Гюйгенс-Штейнер теоремасы береді: дененің кез келген өске қатысты инерция моменті оның массалар центрі арқылы берілген өске параллель өтетін өске қатысты инерция моментіне дене массасын өстер арасындағы қашықтық квадратына көбейтіп қосқанға тең.
Сонымен, Гюйгенс-Штейнер теоремасы былай жазылады:
 , (10)
, (10)
мұндағы 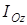 - дененің кез келген Oz өсіне қатысты инерция моменті,
- дененің кез келген Oz өсіне қатысты инерция моменті,  - дененің массалар центрі арқылы Oz өсіне параллель өтетін Cz| өсіне қатысты инерция моменті, М – дененің массасы, ал d – Oz және Cz| өстері арасындағы қашықтық
- дененің массалар центрі арқылы Oz өсіне параллель өтетін Cz| өсіне қатысты инерция моменті, М – дененің массасы, ал d – Oz және Cz| өстері арасындағы қашықтық
(10 өрнегінен 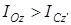 екенін көреміз. Демек, дененің ең кіші инерция моменті массалар центрі арқылы өтетін өске қатысты болады екен.
екенін көреміз. Демек, дененің ең кіші инерция моменті массалар центрі арқылы өтетін өске қатысты болады екен.
Кейбір денелердің өстік инерция моменттері. Кейбір біртекті денелердің инерция моменттерін есептеуге мүмкіндік беретін өрнектерді алайық.
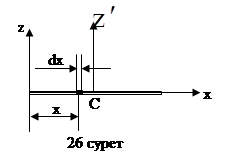 1. Біртекті жіңішке стержень. Ұзындығы
1. Біртекті жіңішке стержень. Ұзындығы 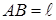 , массасы М біртекті жіңішкестерженьді қарастырайық (26 сурет). Ах өсін стержень бойымен бағыттаймыз. Біртекті стерженнің оның ұшы арқылы стерженьге перпендикуляр өтетін өске қатысты инерция моментінің түрі:
, массасы М біртекті жіңішкестерженьді қарастырайық (26 сурет). Ах өсін стержень бойымен бағыттаймыз. Біртекті стерженнің оның ұшы арқылы стерженьге перпендикуляр өтетін өске қатысты инерция моментінің түрі:
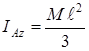 . (11)
. (11)
(10) Гюйгенс-Штейнер теоремасын қолданып, біртекті жіңішке стерженнің оның массалар центрі арқылы стерженьге перпендикуляр өтетін өске қатысты инерция моментін алуға болады
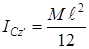 . (12)
. (12)
2. Біртекті жіңішке дөңгелек сақина. Радиусы R, массасы М біртекті сақинаны қарастырып, сақинаның массалар центрі арқылы оған перпендикуляр өтетін 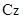 өсіне қатыс- ты инерция моментін табайық. Сақинаның барлық нүктелері
өсіне қатыс- ты инерция моментін табайық. Сақинаның барлық нүктелері 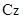 өсінен h = R қашықтықта жатады. Сондықтан (3.8.1) өрнегінен біртекті жіңішке дөңгелек сақинаныңоныңцентрі арқылы сақина жазықтығына перпендикуляр өтетін өске қатысты инерция моментінің өрнегін аламыз:
өсінен h = R қашықтықта жатады. Сондықтан (3.8.1) өрнегінен біртекті жіңішке дөңгелек сақинаныңоныңцентрі арқылы сақина жазықтығына перпендикуляр өтетін өске қатысты инерция моментінің өрнегін аламыз:
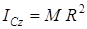 . (13)
. (13)
3. Біртекті дөңгелек диск. Радиусы R, массасы М біртекті жіңішке диск берілсін. Оның массалар центрі арқылы дискіге перпендикуляр өтетін өске қатысты инерция моментін санау үшін дискіні жіңішке сақиналарға бөліп, интегралдар аламыз. Нәтижесінде, біртекті жіңішке дискінің массалар центрі арқылы дискіге перпендикуляр өтетін өске қатысты инерция моменті саналатын өрнек аламыз:
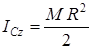 . (14)
. (14)
(14) өрнегімен радиусы R және массасы М біртекті цилиндрдің оның Oz симметрия өсіне қатысты инерция моменті де саналады.
Негізгі әдебиеттер: 4 [IІІ бөлім, 17 тарау, 168-172б], 8 [IV бөлім, §§129-132].
Қосымша әдебиеттер: 11 [IІІ бөлім, 3 тарау, §§1-4, 272-281б].
Бақылау сұрақтары:
Механикалық жүйе. Жүйе массасы.
Жүйе массасының центрі және оның координаталары.
Жүйеге әсер ететін күштердің классификациясы: сыртқы және ішкі күштер, берілген (актив) және байланыс реакциялары
Ішкі күштердің қасиеттері.
Жүйенің және қатты дененің өске қатысты инерция моменті; олардың координата өстеріне қатысты аналитикалық өрнектері.
Инерция радиусы.
Гюйгенс-Штейнер теоремасы.
Кейбір денелердің өстік инерция моменттері.
ДӘРІС-14.Жүйе динамикасының жалпы теоремалары.
Берілген күштер мен бастапқы шарттар бойынша механикалық жүйенің қозғалысын табу үшін жүйенің әрбір нүктесінің қозғалысын білу міндет емес.Жүйе динамикасының жалпы теоремаларының көмегімен жүйе қозғалысын толығымен зерттеуге болады.
1. Механикалық жүйе қозғалысының дифференциалдық теңдеулері. n материялық нүктеден тұратын жүйені қарастырайық. Байланыстарды олардың реакцияларымен алмастырамыз. Жүйенің k-номерлі нүктесіне әсер ететін барлық сыртқы және ішкі күштердің тең әсерлі күштерін 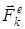 және
және  арқылы белгілейміз. Енді әр нүкте үшін Ньютонның екінші заңын жазайық:
арқылы белгілейміз. Енді әр нүкте үшін Ньютонның екінші заңын жазайық:
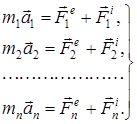 (1)
(1)
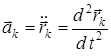 болғандықтан, (1)-жүйе дифференциалдық теңдеулер жүйесі болады. Олар механикалық жүйе қозғалысының дифференциалдық теңдеуінің векторлық түрін береді. Бұл теңдеулердің саны жүйедегі нүктелердің санына, яғни n-ге, тең.
болғандықтан, (1)-жүйе дифференциалдық теңдеулер жүйесі болады. Олар механикалық жүйе қозғалысының дифференциалдық теңдеуінің векторлық түрін береді. Бұл теңдеулердің саны жүйедегі нүктелердің санына, яғни n-ге, тең.
(1) теңдеулерін декарттық координата өстеріне проекциялап, механикалық жүйе қозғалысының осы өстерге проекцияланған 3n дифференциалдық теңдеулерін алуға болады.
1. Механикалық жүйенің массалар центрінің қозғалысы туралы теорема. Көп жағдайда жүйенің қозғалыс сипатын анықтау үшін оның массалар центрінің қозғалыс заңын білу керек болады. Осы заңды анықтау үшін механикалық жүйе қозғалысының дифференциалдық теңдеулерін (1) түрінде құрып, оның оң жағы мен сол жағын қосайық:
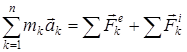 . (2)
. (2)
Осы теңдеудің сол жағын түрлендіріп, барлық ішкі күштердің қосындысының нөлге тең болатынын ескерсек жүйенің массалар центрінің қозғалысы туралы теореманы аламыз:
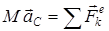 . (3)
. (3)
Теорема: жүйе массасы мен оның массалар центрі үдеуінің көбейтіндісі жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысына тең.
(3) векторлық теңдеуі оның декарттық координата өстеріне проекциялары болатын үш скаляр теңдеуге пара пар болады:
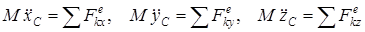 . (4)
. (4)
(4) теңдеулерінің шешімі жүйенің массалар центрінің қозғалыс заңы болады. Егер дене ілгерілемелі қозғалса, массалар центрінің қозғалысы оның қозғалысын толық анықтайды.
Жүйенің массалар центрінің қозғалысы туралы теореманың салдары:
1. Егер жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысы нөлге тең болса, онда жүйенің массалар центрі тыныштықта болады немесе бірқалыпты түзу сызықты қозғалады.
2. Егер жүйеге әсер ететін барлық сыртқы күштердің бір өске проекциясы нөлге тең болса, онда жүйенің массалар центрінің жылдамдығының осы өске проекциясы өзгермейді.
3. Жүйенің массалар центрінің қозғалысын ешқандай ішкі күштермен өзгертуге болмайды. Атап айтқанда, ішкі күштер жүйенің массалар центрінің тепе теңдігін бұза алмайды. Ішкі күштер жүйенің массалар центрінің қозғалысына тек сыртқы күштер арқылы әсер ете алады.
1. Механикалық жүйенің қозғалыс мөлшері. Біз нүктенің қозғалыс мөлшеріоның массасы мен жылдамдық векторының көбейтіндісіне тең екенін білеміз. Механикалық жүйенің қозғалыс мөлшері деп жүйедегі барлық нүктелердің қозғалыс мөлшерлерінің геометриялық қосындысына тең  векторын айтады:
векторын айтады:
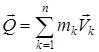 . (5)
. (5)
Жүйенің қозғалыс мөлшерініңвекторын мына түрде де жазуға болады
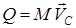 , (6)
, (6)
демек, жүйенің қозғалыс мөлшері бүкіл жүйенің массасы мен оның массалар центрі жылдамдығының көбейтіндісіне тең.
Механикалық жүйенің қозғалыс мөлшері жүйенің массалар центрімен бірге ілгерілемелі қозғалысын сипаттайды.
1. Жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема. n материялық нүктеден тұратын механикалық жүйені қарастырып, оның қозғалысының (1) дифференциалдық теңдеулерін 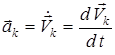 екенін ескеріп жазайық. Барлық теңдеулерді қосып, алынған теңдіктің сол жағын түрлендірсек және жүйенің ішкі күштерінің қасиетін ескерсек жүйеніңқозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық түрін аламыз:
екенін ескеріп жазайық. Барлық теңдеулерді қосып, алынған теңдіктің сол жағын түрлендірсек және жүйенің ішкі күштерінің қасиетін ескерсек жүйеніңқозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық түрін аламыз:
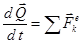 . (7)
. (7)
Теорема: механикалық жүйенің қозғалыс мөлшері векторының уақыт бойынша туындысы жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысына тең.
(3) теңдеуі декарттық координата жүйесінің өстеріне проекцияланған үш скаляр теңдеуге пара пар:
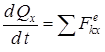 ,
, 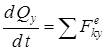 ,
, 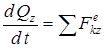 . (8)
. (8)
Осы теореманы басқа түрде жазуға болады. Механикалық жүйенің бастапқы 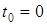 уақыттағы қозғалыс мөлшерін
уақыттағы қозғалыс мөлшерін 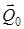 деп, ал
деп, ал  уақыттағы қозғалыс мөлшерін
уақыттағы қозғалыс мөлшерін 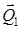 деп белгілеп, (7) теңдеуін интегралдайық, сонда
деп белгілеп, (7) теңдеуін интегралдайық, сонда
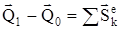 , (9)
, (9)
(9) – жүйенің қозғалыс мөлшерінің өзгеруі туралы теореманың интегралдық түрі:кез келген уақыт аралығындағы жүйенің қозғалыс мөлшерінің өзгеруі осы уақыт аралығында жүйеге әсер ететін барлық сыртқы күштердің импульстерінің геометриялық қосындысына тең.
Есеп шығарғанда (9) векторлық теореманы декарттық координата жүйесінің өстеріне проекциялау керек:
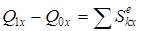 ,
, 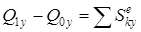 ,
, 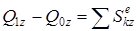 . (10)
. (10)
Жүйенің қозғалыс мөлшерінің өзгеруі туралы теоремадан қозғалыс мөлшерініңсақталу заңдарын аламыз:
Егер жүйеге әсер ететін барлық сыртқы күштердің геометриялық қосындысы нөлге тең болса, онда жүйенің қозғалыс мөлшерінің векторының шамасы да, бағыты да өзгермейді.
Егер жүйеге әсер ететін барлық сыртқы күштердің бір өске проекциясының қосындысы нөлге тең болса, онда жүйенің қозғалыс мөлшерінің осы өске проекциясы тұрақты болады.
Бұл заңдардан ішкі күштер жүйенің қозғалыс мөлшерін өзгерте алмайтынын көреміз.
1. Механикалық жүйенің кинетикалық моменті. Жүйенің қозғалыс мөлшерінің векторы жүйенің ілгерілемелі қозғалысын сипаттайды. Жүйенің айналмалы қозғалысы кинетикалық момент деп аталатын шамамен сипатталады.
Бір материялық нүктенің О центріне қатысты қозғалыс мөлшерінің моменті былай анықталады: 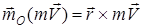 . Механикалық жүйенің О центріне қатысты қозғалыс мөлшерінің бас моменті (немесекинетикалық моменті) деп жүйедегі барлық нүктелердің қозғалыс мөлшерлерінің сол нүктеге қатысты моменттерінің геометриялық қосындысын айтады:
. Механикалық жүйенің О центріне қатысты қозғалыс мөлшерінің бас моменті (немесекинетикалық моменті) деп жүйедегі барлық нүктелердің қозғалыс мөлшерлерінің сол нүктеге қатысты моменттерінің геометриялық қосындысын айтады:
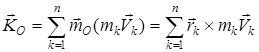 . (11)
. (11)
Мұндағы  – басы О центрінде болатын
– басы О центрінде болатын 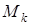 материялық нүктенің радиус-векторы, mk мен
материялық нүктенің радиус-векторы, mk мен 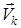 – осы нүктенің массасы мен жылдамдығы.
– осы нүктенің массасы мен жылдамдығы.
Вектор болғандықтан, 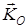 кинетикалық момент проекцияларымен берілуі мүмкін. Атап айтқанда, (11) теңдеуінің декарттық координата өстеріне проекциялары былай жазылады:
кинетикалық момент проекцияларымен берілуі мүмкін. Атап айтқанда, (11) теңдеуінің декарттық координата өстеріне проекциялары былай жазылады:
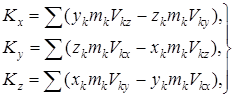 (12)
(12)
мұндағы xk , yk , zk – Mk нүктесінің координаталары
(12) – механикалық жүйенің координата өстеріне қатыстыкинетикалық моменттері.
Жеке жағдайда, айналмалы қозғалыстағы қатты дененің айналу өсіне қатыстыкинетикалық моменті мына өрнекпен анықталады:
 . (13)
. (13)
Демек, айналмалы қозғалыстағы қатты дененің айналу өсіне қатысты кинетикалық моменті дененің осы өске қатысты инерция моменті мен осы өске проекцияланған дененің бұрыштық жылдамдығының көбейтіндісіне тең екен.
1. Жүйенің кинетикалық моментінің өзгеруі туралы теорема. n материялық нүктеден тұратын жүйеге әсер ететін барлық күштер мен реакция күштерін сыртқы және ішкі күштерге бөлейік. Сонда жүйенің k-нүктесі үшін О центріне қатысты кинетикалық моменттің өзгеруі туралы теорема былай жазуға болады:
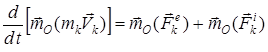 ,
,
мұндағы 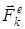 мен
мен  – осы нүктеге әсер ететін барлық сыртқы және ішкі күштердің тең әсерлілері.
– осы нүктеге әсер ететін барлық сыртқы және ішкі күштердің тең әсерлілері.
Осы теореманы жүйенің барлық нүктелері үшін жазып, оларды қосуға болады. Нәтижесінде мынаны аламыз:
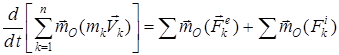 .
.
Бұл өрнектегі соңғы қосылғыш ішкі күштердің қасиеті бойынша нөлге тең, ал дифференциал астындағы өрнек жүйенің О центріне қатысты кинетикалық моменті 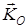 . Сонымен, жүйенің кинетикалық моментінің өзгеруі туралы теореманы аламыз:
. Сонымен, жүйенің кинетикалық моментінің өзгеруі туралы теореманы аламыз:
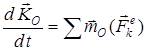 . (14)
. (14)
Теорема: механикалық жүйенің О центріне қатысты кинетикалық моментінің уақыт бойынша туындысы жүйеге әсер ететін барлық сыртқы күштердің сол центрге қатысты моменттерінің геометриялық қосындысына тең.
(14) теңдеуін координата өстеріне проекциялап, өстерге қатысты моменттер теоремасын аламыз:
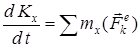 ,
,  ,
, 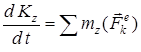 . (15)
. (15)
Бұл теорема дененің айналмалы қозғалысын зерттеуде, гироскоптар теориясында, соққы теориясында кеңінен қолданылады.
Жүйенің кинетикалық моментінің сақталу заңдары:
Егер барлық сыртқы күштердің бір центрге қатысты моменттерінің геометриялық қосындысы нөлге тең болса, онда жүйенің осы центрге қатысты кинетикалық моментінің шамасы да, бағыты да өзгермейді.
Егер сыртқы күштердің бір центрге қатысты моменттерінің қосындысы нөлге тең болса, онда жүйенің осы центрге қатысты кинетикалық моменті тұрақты болады.
Негізгі әдебиеттер: 4 [IІІ бөлім, 17 тарау, 177-182б], 8 [IV бөлім, §§134-140].
Қосымша әдебиеттер: 11 [IІІ бөлім, 4 тарау, §§1-4, 293-315, 326-336б].
Бақылау сұрақтары:
Механикалық жүйе қозғалысының дифференциалдық теңдеулері.
Жүйенің массалар центрінің қозғалысы туралы теорема.
Массалар центрі қозғалысының сақталу заңы.
Жүйенің қозғалыс мөлшері.
Жүйенің қозғалыс мөлшерінің өзгеруі туралы теорема; сақталу заңы.
Жүйенің қозғалыс мөлшерінің бас моменті немесе кинетикалық моменті.
Қатты дененің өсті айнала қозғалысының кинетикалық моменті.
Жүйенің кинетикалық моментінің өзгеруі туралы теорема; сақталу заңы.
ДӘРІС-15.Жүйе динамикасының жалпы теоремалары (жалғасы).
2.6.1 Жүйе мен қатты дененің кинетикалық энергиясы. Бір нүктенің кинетикалық энергиясы 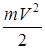 өрнегімен анықталады. Жүйенің кинетикалық энергиясы деп жүйедегі барлық нүктелердің кинетикалық энергияларының қосындысына тең Т скаляр шаманы айтады
өрнегімен анықталады. Жүйенің кинетикалық энергиясы деп жүйедегі барлық нүктелердің кинетикалық энергияларының қосындысына тең Т скаляр шаманы айтады
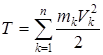 . (16)
. (16)
Жүйенің кинетикалық энергиясы жүйенің қозғалыс бағытына тәуелді емес, ол жүйенің ілгерілемелі қозғалысын да, айналмалы қозғалысын да сипаттайды.
Көбінесе механикалық жүйе қатты денеден немесе қатты денелердің жиынтығынан құралады. Осыған байланысты әртүрлі қозғалыстағы қатты дененің кинетикалық энергиясын санау қажет болады.
Қатты дененің ілгерілемелі қозғалысы. Біз мұндай қозғалыстағы дененің барлық нүктелерінің жылдамдықтарының бірдей болатынын кинематикадан білеміз. Демек, кез келген k нүкте үшін 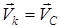 , бұл жерде
, бұл жерде 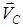 – дененің массалар центрінің жылдамдығы. (16) өрнегінен мынаны аламыз:
– дененің массалар центрінің жылдамдығы. (16) өрнегінен мынаны аламыз:
 , (17)
, (17)
мұндағы М – дененің массасы.
Сонымен, ілгерілемелі қозғалыстағы қатты дененің кинетикалық энергиясы дененің массасы мен оның массалар центрі жылдамдығы квадраты көбейтіндісінің жартысына тең.
Қатты дененің айналмалы қозғалысы. Егер дене қозғалмайтын Oz өсімен айналатын болса, онда оның айналу өсінен hk қашықтықтағы кез келген 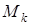 нүктесінің жылдамдығы
нүктесінің жылдамдығы  болады. Жылдамдықтың осы мәнін (16)-ға қойсақ:
болады. Жылдамдықтың осы мәнін (16)-ға қойсақ:
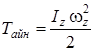 , (18)
, (18)
яғни айналмалы қозғалыстағы қатты дененің кинетикалық энергиясы дененің айналу өсіне қатысты инерция моменті мен бұрыштық жылдамдықтың квадратының көбейтіндісінің жартысына тең.
Қатты дененің жазық-параллель қозғалысы. Біз қатты дененің жазық-параллель қозғалысын оның полюспен бірге ілгерілемелі қозғалысы мен полюс төңірегіндегі айналмалы қозғалысының қосындысы деп қарастыруға болатынын кинематикадан білеміз. Полюс ретінде дененің массалар центрін алған ыңғайлы. Сонда
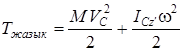 . (19)
. (19)
Жазық-параллель қозғалыстағы қатты дененің кинетикалық энергиясы оның массалар центрімен бірге ілгерілемелі қозғалысының кинетикалық энергиясы мен центр арқылы қозғалыс жазықтығына перпендикуляр өтетін өске қатысты айналмалы қозғалысының кинетикалық энергиясының қосындысына тең.
Егер жүйе бірнеше денеден тұрса, онда оның Т кинетикалық энергиясы жүйедегі барлық денелердің 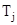 кинетикалық энергияларының қосындысына тең:
кинетикалық энергияларының қосындысына тең:
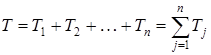 .
.
3.15.2 Жүйеге әсер ететін күштердің жұмысы мен қуаты. Механикалық жүйе қозғалысын зерттегенде жүйеге әсер ететін күштердің жұмысын санау қажеттілігі пайда болады. Күш жұмысын санаудың кейбір дербес жағдайларын қарастырамыз.
1. Ауырлық күшінің жұмысы. Біртекті салмақ өрісіндегі жүйенің әрбір 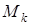 нүтесіне ауырлық күші әсер етеді. Жүйе бастапқы орыннан шекті орынға орын ауыстырғанда ауырлық күшінің толық жұмысы мына өрнекпен анықталады (z өсі вертикаль жоғары бағытталған):
нүтесіне ауырлық күші әсер етеді. Жүйе бастапқы орыннан шекті орынға орын ауыстырғанда ауырлық күшінің толық жұмысы мына өрнекпен анықталады (z өсі вертикаль жоғары бағытталған):
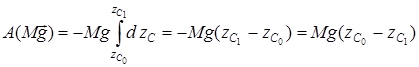 .
.
Бұл өрнектегі 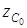 мен
мен 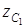 – жүйенің zC ауырлық центрі координатасының бастапқы және шекті орындардағы мәндері.
– жүйенің zC ауырлық центрі координатасының бастапқы және шекті орындардағы мәндері.
Енді жүйенің массалар центрінің hC орын ауыстыру биіктігі ұғымын ендірейік:
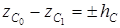 ,
,
нәтижесінде механикалық жүйенің ауырлық күші жұмысының өрнегін аламыз:
 , (20)
, (20)
демек, жүйенің ауырлық күшінің жұмысы плюс немесе минус таңбасымен алынған бүкіл жүйе салмағы мен жүйенің ауырлық центрінің вертикаль орын ауыстыруының көбейтіндісіне тең. Плюс таңбасы жүйенің ауырлық центрі төмен қарай орын ауыстырғанда, ал минус таңбасы – жоғары қарай орын ауыстырғанда алынады.
2. Айналмалы қозғалыстағы денеге әсер ететін күштің жұмысы. Дененің z айналу өсінен h қашықтықта жатқан кез келген нүктеге 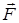 күші түсірілсін.
күші түсірілсін.
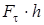 көбейтіндісін Mz арқылы белгілеп, айналдырушы момент деп атаймыз. Сонда дене шекті бұрышқа бұрылғанда
көбейтіндісін Mz арқылы белгілеп, айналдырушы момент деп атаймыз. Сонда дене шекті бұрышқа бұрылғанда 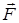 күшінің жұмысы төмендегі өрнекпен анықталатынын аламыз:
күшінің жұмысы төмендегі өрнекпен анықталатынын аламыз:
 , (21)
, (21)
мұндағы j1 – дененің айналу бұрышы.
Егер қозғалыс барысында күш моменті өзгермесе, яғни  болса, онда
болса, онда
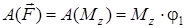 , (22)
, (22)
яғни, айналмалы қозғалыстағы денеге әсер ететін тұрақты моменттің жұмысы осы момент пен дененің айналу бұрышының көбейтіндісіне тең.
Бұл жағдайда күш қуаты мынандай болады:
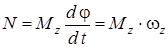 . (23)
. (23)
Домалау үйкелісі моментінің жұмысы. Бізге статикадан шамасы 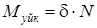 тең, бір дененің екінші бір дене бетімен домалаған кезде домалау үйкелісі моментінің пайда болатыны белгілі (d – домалау үйкелісінің коэффициенті).
тең, бір дененің екінші бір дене бетімен домалаған кезде домалау үйкелісі моментінің пайда болатыны белгілі (d – домалау үйкелісінің коэффициенті).
Егер R - домалайтын дененің радиусы, N - нормаль реакция, SC - дененің массалар центрінің өтетін жолы деп алсақ, онда домалау үйкелісі моментінің жұмысын былай жазуға болады:
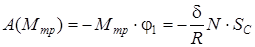 (24)
(24)
Жүйенің кинетикалық энергиясының өзгеруі туралы теорема. Егер жүйенің k-нөмірлі нүктесін қарастырсақ, онда бұл нүкте үшін кинетикалық энергияның өзгеруі туралы теорема орын алады. Егер 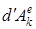 мен
мен 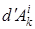 – осы нүктеге әсер ететін сыртқы және ішкі күштердің элементар жұмыстары деп алсақ, онда бұл теореманың дифференциалдық түрі:
– осы нүктеге әсер ететін сыртқы және ішкі күштердің элементар жұмыстары деп алсақ, онда бұл теореманың дифференциалдық түрі:
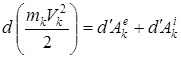 .
.
Осындай теоремаларды жүйенің барлық нүктелері үшін жазуға болады. Бұл теоремаларды қоссақ нәтижесінде мына өрнекті аламыз:
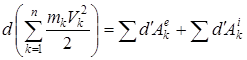
немесе (16) өрнегін ескерсек
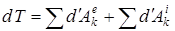 . (25)
. (25)
(25) өрнек жүйенің кинетикалық энергиясының өзгеруі туралы теореманың дифференциалдық түрін білдіреді.
Жүйенің кинетикалық энергиясы Т0 –ге тең болатын 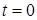 бастапқы уақыт пен жүйенің кинетикалық энергиясы Т1 –ге тең болатын
бастапқы уақыт пен жүйенің кинетикалық энергиясы Т1 –ге тең болатын  шекті уақытты қарастырайық. Жүйе бастапқы орыннан шекті орынға орын ауыстырғанда (25) өрнегінің екі жағынан да интеграл алсақ, жүйенің кинетикалық энергиясының өзгеруі туралы теореманың интегралдық (шекті) түрін аламыз:
шекті уақытты қарастырайық. Жүйе бастапқы орыннан шекті орынға орын ауыстырғанда (25) өрнегінің екі жағынан да интеграл алсақ, жүйенің кинетикалық энергиясының өзгеруі туралы теореманың интегралдық (шекті) түрін аламыз:
 , (26)
, (26)
демек жүйе шекті орын ауыстырғандаоның кинетикалық энергиясының өзгеруі осы орын ауыстыруда жүйеге әсер ететінбарлық сыртқы және ішкі күштердің жұмыстарының қосындысына тең.
Негізгі әдебиеттер: 8 [IV бөлім, §§147-149].
Қосымша әдебиеттер: 11 [IІІ бөлім, 4 тарау, §5, 338-341б].
Бақылау сұрақтары:
1. Механикалық жүйенің кинетикалық энергиясы.
2. Әртүрлі қозғалыстағы қатты дененің кинетикалық энергиясы.
3. Айналмалы қозғалыстағы қатты денеге түсірілген күштің жұмысы мен қуаты.
4. Механикалық жүйенің кинетикалық энергиясының өзгеруі туралы теорема.
Дата добавления: 2015-06-17; просмотров: 4621;
