Тәжірибелік сабақтардың жоспарлары

Модуль №1 «Статика»

ТӘЖІРИБЕЛІК САБАҚ-1.Жинақталатын күштер жүйесі.

Тапсырма: Жинақталған күштер жүйесінің тепе-теңдігінің аналитикалық шарттарын есеп шығаруда пайдалана білу.

Әдістемелік ұсыныстар:Берілген тақырып бойынша есептер шығару үшін студент

36. статиканың негізгі ұғымдары мен анықтамаларын, статиканың аксиомаларын;

37. байланыс реакцияларының негізгі түрлерін;

38. күштерді өстерге проекциялауды;

39. денелердің тепе-теңдік шарттарын

білуі керек.

Есептерді шығару реті:

Тепе-теңдігі қарастырылатын нүктені немесе денені белгілеу.

Денені байланыстардан босатып, суретте оған әсер етуші актив күштер мен байланыс реакцияларын кескіндеу.

Координат жүйесін енгізіп, тепе-теңдік теңдеулерін құру. Жинақталған күштер жүйесі үшін координата осінің біреуін белгісіз реакцияның әсер ету сызығы бойымен бағыттасақ, онда құрылған теңдеулерді шешу жеңіл болады.

Егер денеге тек үш күш қана әсер етсе, онда геометриялық әдісті қолданған дұрыс. Бұл жағдайда тепе-теңдік теңдеулерінің орнына күштер үшбұрышы салынады. Күштер үшбұрышын белгілі күштен бастап салған жөн. Ізделінді шамалар күштер үшбұрышынан синустар (немесе косинустар) теоремасының көмегімен анықталады.

Есептер шығару үлгілері.

Есеп №1. Салмағы 10 Н біртекті шарды вертикаль жазықтықта өзара 150° бұрыш құратын АВ және СD тростары ұстап тұр. АВ тросы горизонтпен 60°

бұрыш құрайды (1а сурет). Тростардың керу күштерін табыңдар.

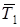Шешімі. Шарды О материялық нүкте деп есептеп, оны байланыстардан босатып, байланыстардың денеге әсерін реакциялармен алмастырайық. Енді О нүктесін бір нүктеге жинақталатын үш жазық күш әсер ететін еркін нүкте деп қарастыруға болады: актив күш және СD мен АВ тростарының керу күштері мен 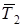. Бұл реакция күштері тростардың бойымен бағытталған. , , 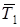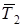- жинақталған күштер жүйесін құрайды (1ә сурет).

Есепті шығарудың екі жолын қарастырайық.

1. Геометриялық әдіс.

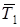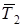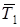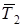, және күштері тепе-теңдікте болғандықтан, осы күштерден құрылған күштер үшбұрышы тұйық болады(2-сурет). Алдымен шамасы мен бағыты белгілі күшін салайық. Бұл күштің екі ұшы арқылы және күштеріне тең және оларға параллель екі кесінді жүргіземіз (1б сурет). Алынған масштабқа сай тұйық күш үшбұрышының DС және АВ қабырғалары тростардың реакцияларының бағыты мен шамасын береді (Графиктік әдіс ).

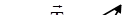Күш үшбұрышынан салу бойынша DС=АС, яғни ,

.

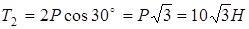Немесе синустар теоремасын пайдалансақ

; .

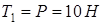2. Аналитикалық әдіс.

Күштердің координат өстеріне қатысты проекциялары ыңғайлы болатындай координат жүйесі енгізіледі (3-сурет). Берілген есепте координат жүйесінің бас нүктесі ретінде О нүктесін алып, жинақталатын жазық күштер жүйесінің тепе-

теңдік шарттарын жазамыз:

.

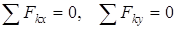Барлық күштердің координат осьтеріне проекцияларын тауып, олардың алгебралық қосындысын нөлге теңестірейік:

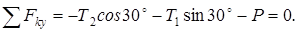
Осы теңдеулер жүйесінен белгісіз реакциялар ;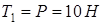

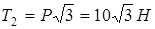
түріндеанықталады.

Есеп № 2. 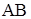арқалық А нүтесінде жылжымайтын топсамен, ал В нүктесінде жылжымалы цилиндрлік топсамен бекітілген. Арқалықтың О нүктесіне арқалық өсіне 45° бұрышпен орналасқан 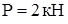күш әсер етеді (4- сурет). Тірек реакцияларын анықтаңдар, мұндағы .

Шешімі. АВ арқалықтың тепе-теңдігін қарастырамыз. Оған әсер ететін байланыстарды алып тастап (А және В топсалары), оларды реакцияларымен алмастырамыз. Жылжымайтын цилиндрлік топсаның реакциясы координата өстерінің бойымен бағытталған екі құраушыдан тұрады, ал жылжымалы цилиндртік топсаның реакциясы тіреуші бетке перпендикуляр бағытталған. Белгісіздер саны теңдеулер санынан артық болғандықтан үш күш туралы теореманы пайдаланамыз.

А топсасындағы реакция күшінің екі құраушысы бір тең әсерлі күшке келеді. Демек үш күш туралы теорема бойынша бұл күштердің әсер ету сызықтары бір нүктеде қиылысады. Бағыттары белгілі күштердің ( 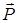және 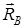) әсер ету сызықтарын созып С қиылысу нүктесін табуға болады. Ізделінді үшінші күштің 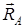әсер ету сызығы осы С нүктесінен өтуі керек (4-сурет). 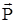күшінің модулін және басқа екі күштің ( 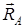және 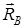) бағыттарын біле отырып, соңғы күштердің модулдерін табуға болады.

Алынған жинақталған күштер жүйесі үшін тепе-теңдік теңдеулерін құрамыз:

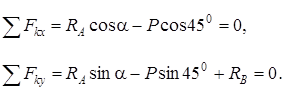
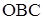үшбұрышынан

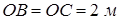екендігі шығады, ал 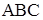үшбұрышынан

.

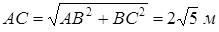Демек

.

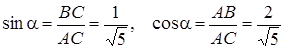Сонымен

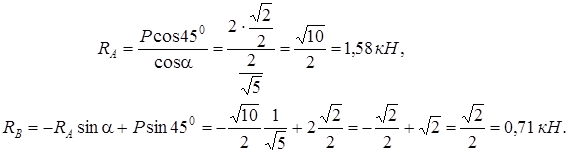
Негізгі әдебиет 6 [№№ 2.8; 2.20; 2.29; 2.31(а); 2.33].

Қосымша әдебиет 13 [5-10, 22-34б].

Бақылау сұрақтары:

Байланыстар және олардың реакциялары.

Жинақталатын күштер жүйесінің тепе-теңдігінің геометриялық шарты.

Күштің өстерге проекциялары.

4. Жинақталатын күштер жүйесінің тепе-теңдігінің аналитикалық шарттары.

5.Параллель емес үш күш туралы теорема.

ТӘЖІРИБЕЛІК САБАҚ-2, 3.Кез келген жазық күштер жүйесі. Денелер жүйесінің тепе-теңдігі.

Тапсырма: Кез келген бағыттағы күштер жүйесінің тепе-теңдігінің аналитикалық шарттарын есеп шығаруда пайдалана білу. Денелер жүйесінің тепе-теңдік шарттарын қанағаттандыратын белгісіз күштерді табу.

Әдістемелік ұсыныстар:Берілген тақырып бойынша есептер шығару үшін студент

40. нүктеге қатысты күш моментін;

41. кез келген жазық күштер жүйесінің аналитикалық тепе-теңдік шарттарын;

42. жазықтықтағы параллель күштер жүйесінің тепе-теңдік шарттарын;

43. таралған күштерді бір нүктеге түскен күшке келтіруді;

44. денелер жүйесінің тепе-теңдік шарттарын

білуі керек.

Есептерді шығару реті:

1. Тепе-теңдігі қарастырылатын нүктені немесе денені белгілеу.

2. Денені байланыстардан босатып, суретте оған әсер етуші актив күштер мен байланыс реакцияларын кескіндеу.

3. Декарт координата өстерін таңдап алу.

4. Актив күштерімен қатар реакция күштерін де қамтитын жазық күштер жүйесі үшін тепе-теңдік теңдеулерін құру.