Ші модуль. ДИНАМИКА

ДӘРІС-10.Динамика. Материалық нүкте динамикасы.

3.10.1 Динамикаға кіріспе.Динамика – күш әсерінен материялық денелердің қозғалысын зерттейтін теориялық механиканың бөлімі. Динамикада тек тұрақты күштер ғана емес, сонымен бірге уақытқа, координаталарға және жылдамдыққа тәуелді айнымалы күштер де қарастырылады. Айнымалы күштер тұрақты күштердің заңдарына бағынады, яғни оларды қосуға, жіктеуге болады, олардың моменттері және т.б. болады.

3.10.2 Материялық нүкте динамикасы. Материялық нүкте деп қозғалысын зерттегенде өлшемдерін ескермеуге болатын материялық денені айтады.

3.10.2.1 Материялық нүкте динамикасының негізгі заңдары. Ньютонның үш заңы материялық нүкте динамикасының негізгі заңдары болып табылады.

Ньютонның бірінші заңы.Егер материялық нүктеге сырттан ешбір күш әсер етпесе немесе әсер ететін күштер жүйесі нөлге пара-пар болса, онда нүкте тыныштық күйде немесе бірқалыпты және түзу сызықты қозғалыста болады. Ньютонның бірінші заңы орындалатын санақ жүйелері инерциялық санақ жүйелері деп аталады.

Ньютонның екінші заңы (динамиканың негізгі заңы). Материялық нүктенің үдеуі оған әсер етуші күшке тура пропорционал, бағыты күшпен бағыттас. Нүкте массасы пропорционалдық коэффициент болып табылады.

Бұл заңның математикалық өрнегі:

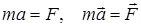. (1)

Егер денеге бірнеше 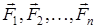күштер әсер етсеНьютонның екінші заңы былай жазылады:

. (2)

Ньютонның үшінші заңы.Екі материялық нүкте бір-біріне модульдері тең, бір түзудің бойымен қарама-қарсы бағытталған күштермен әсер етеді.

3.10.2.2 Нүкте динамикасының негізгі мәселелері. Материялық нүктенің негізгі мәселелері еркін және еркін емес нүктелер үшін айтылады..

Қозғалысы басқа денелермен шектелмеген нүктені еркін материялық нүкте дейміз. Осындай нүкте үшін динамиканың екі негізгі мәселесі қарастырылады:

Динамиканың бірінші негізгі мәселесі:Нүктенің массасы мен қозғалыс заңын біле отырып, оған әсер ететін күштерді анықтау.

Динамиканың екінші негізгі мәселесі:Нүктенің массасы мен оған әсер ететін күштерді біле отырып, оның қозғалыс заңын анықтау.

Екі мәселе де Ньютонның екінші (2) заңының көмегімен шешіледі.

Қозғалысы басқа денелермен шектелген нүкте еркін емес материялық нүкте деп аталады. Мұндай нүкте үшін оған әсер ететін барлық актив 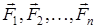күштерге реакция күштерін қосу қажет. Оларды бір күшпен белгілейміз. Сонда Ньютонның екінші заңы былай жазылады:

. (3)

(3) өрнегімен еркін емес нүкте үшін де динамиканың екі негізгі мәселесі шешіледі:

Динамиканың бірінші негізгі мәселесі:Нүктенің массасын, қозғалыс заңын және оған әсер ететін актив күштерді біле отырып, реакция күштерін анықтау.

Динамиканың екінші негізгі мәселесі:Нүктенің массасын және оған әсер ететін актив күштерді біле отырып, оның қозғалыс заңын және реакция күштерін анықтау.

Нүкте динамиканың бірінші негізгі мәселесінің шешуі. Бұл мәселені шешу үшін Ньютонның екінші заңын құрып, сосын оны координата өстеріне проекциялау керек.

3.10.2.3 Материялық нүкте қозғалысының дифференциалдық теңдеулерін интегралдау. Материялық нүктенің инерциялық санақ жүйесіндегі орнын 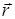радиус-векторымен анықтаймыз. Нүктеге әсер ететін күш жалпы жағдайда t уақытқа, нүктенің орнына, яғни 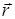радиус-векторға және 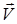нүктенің жылдамдығына тәуелді бола алады, яғни 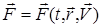. Егер нүктенің үдеуі 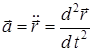, ал жылдамдығы екенін ескерсек, Ньютонның екінші заңы немесе нүкте динамикасының негізгі теңдеуі мына түрде жазылады:

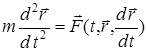. (4)

Бұл теңдеу векторлық түрдегі нүкте қозғалысының дифференциалдық теңдеуі деп аталады.

(4) теңдеуі декарттық координата жүйесінің өстеріне проекцияланған үш скалярлық теңдеуге пара-пар:

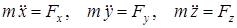. (5)

Нүкте динамикасының екінші мәселесінің шешуі белгісіз x, y, z функцияларына қатысты екінші дәрежелі үш дифференциалдық теңдеулер жүйесінен тұратын оның қозғалысының дифференциалдық (5) теңдеулерін интегралдауға тіреледі.

Бұл теңдеулердің жалпы шешімі С₁, С₂, …, С₆ алты интегралдық тұрақтыларға тәуелді:

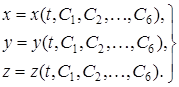(6)

Интегралдық тұрақтылар әртүрлі мәнге ие бола алады, сондықтан бірдей күш әсер ететін нүкте түрлі қозғалыс жасай алады. Сонымен, нүкте қозғалысының нақты заңын анықтау үшін тек күштің берілуі жеткіліксіз екен. Интегралдық тұрақтылар бастапқы уақытқа байланысты шарттардан

t=0: 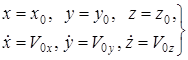(7)

табылады

. (8)

Табылған тұрақтыларды (6) жалпы шешімге қойып, берілген бастапқы шарттарға сәйкес келетін есептің шешуін аламыз.

Негізгі әдебиеттер: 4 [IІІ бөлім, 13 тарау, 128-138б], 8 [IІІ бөлім, §§99-108].

Қосымша әдебиеттер: 11 [IІІ бөлім, 1 тарау, §§1-5, 235-247б].

Бақылау сұрақтары:

Динамика нені зерттейді?

Ньютонның заңдары.

Еркін және еркін емес материялық нүкте үшін динамиканың негізгі мәселелері.

ДӘРІС-11.Нүкте динамикасының жалпы теоремалары.

Нүкте динамикасының есептерін шығарғанда нүкте қозғалысының дифференциалдық теңдеулерін интегралдау қажет. Көп жағдайда бұл теңдеулерді интегралдау оңай емес. Сондықтан нүкте динамикасының жалпы теоремаларын пайдаланады

3.11.1 Нүктенің қозғалыс мөлшері. Күш импульсі. Нүкте қозғалысының негізгі динамикалық сипаттамаларының бірі – қозғалыс мөлшері.

Нүктенің қозғалыс мөлшері деп оның массасы мен жылдамдық векторының көбейтіндісіне тең ( 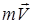) векторлық шаманы айтады. Қозғалыс мөлшерінің векторы әрқашан нүкте жылдамдығымен бағыттас болады.

Белгілі уақыт аралығындағы күштің нүктеге әсерін күш импульсі дейді.

Күштің элементар импульсі деп күш векторының элементар уақытқа көбейтіндісіне тең векторлық шаманы айтады:

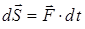(1)

Бұл вектор күштің әсер ету сызығының бойымен бағытталады.

Шекті уақыт аралығындағы күш импульсі 0-ден t₁-ге дейінгі аралықтағы элементар импульстен алынған интегралға тең:

. (2)

Егер күштің сан мәні мен бағыты тұрақты болса ( ), онда .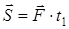

Есеп шығарғанда күш импульсін координата өстеріне проекциялайды, декарттық координата жүйесі үшін бұл проекциялар былай жазылады:

. (3)

1. Нүктенің қозғалыс мөлшерінің өзгеруі туралы теорема. Нүкте үдеуінің векторы жылдамдық векторынан уақыт бойынша алынған бірінші туындыға тең 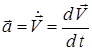екенін ескерсек, нүкте динамикасының негізгі заңын ( ) былай жазуға болады:

. (4)

(4) теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманың дифференциалдық түрін береді:нүктенің қозғалыс мөлшерінің уақыт бойынша бірінші туындысы нүктеге әсер ететін барлық күштердің геометриялық қосындысына тең.

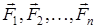күштері әсер ететін М нүктесінің t = 0 ден t = t₁-ге дейінгі шекті уақыт аралығында М₀-ден М₁-ге дейінгі қозғалысын қарастырайық. Оның жылдамдығы 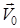-ден 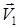-ге дейін өзгерсін. (4) теңдеуіндегі теңдіктің екі жағын да dt-ға көбейтіп, интеграл алайық:

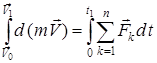немесе .

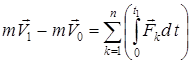Егер (2) өрнегін ескерсек:

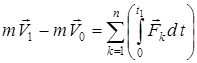. (5)

(5) теңдеуі нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманың интералдық (шекті) түрін береді:шекті уақыт аралығындағы нүктенің қозғалыс мөлшерінің өзгеруі осы уақыт аралығында нүктеге әсер ететін барлық күштер импульстерінің геометриялық қосындысына тең.

Есеп шығарғанда (5) теореманы координата өстеріне проекциялау керек. Декарттық координата жүйесінің өстеріне проекцияласақ:

(6)

1. Нүктенің қозғалыс мөлшерінің моменті және оның өзгеруі туралы теорема. Кейбір есептерде динамикалық сипаттамалар ретінде центрге немесе өске қатысты нүктенің қозғалыс мөлшерінің моменті қарастырылады.

Нүктенің О центріне қатысты қозғалыс мөлшерінің моменті деп

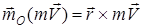(7)

өрнекпен анықталатын 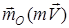векторлық шаманы айтады, мұндағы 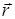- нүктенің О центріне қатыстырадиус-векторы. Бұл вектор 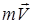векторы мен О центрі арқылы өтетін жазықтыққа перпендикуляр, ұшынан қарағанда 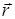векторынан 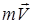векторына қарай ең жақын бұрылу сағат тіліне қарсы болып көрінетіндей бағытталған. Оның сан шамасы , мұндағы h – О центрінен М нүктесінен траекторияға жүргізілен жанама арасындағы ең жақын ара қашықтық (перпендикуляр).

(7) векторының өске проекциясы нүктенің өске қатыстықозғалыс мөлшерінің моментін анықтайды. Декарттық координата жүйесінің өстері үшін, күштердің моменттері сияқты, нүктеніңx, y және z өстеріне қатысты қозғалыс мөлшерінің моменттерінің аналитикалық өрнектерін жазуға болады:

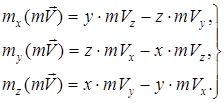(8)

Бұл теңдеулердегі x, y, z – нүкте координаталары, V_x, V_y, V_z – нүкте жылдамдығының координата өстеріне проекциялары.

Нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теорема уақыт өткен сайынғы 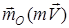векторының өзгеруін анықтайды.

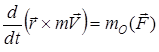. (9)

Бұл теңдеу нүктенің центрге қатысты қозғалыс мөлшері моментінің өзгеруі туралы теореманы білдіреді: нүктенің кез келген О центріне қатысты қозғалыс мөлшері моментінен уақыт бойынша алынған туынды нүктеге әсер ететін күштің осы центрге қатысты моментіне тең.

(9) векторлық теңдеу үш скалярлық теңдеуге пара-пар

(10)

(10) теңдеулері нүктенің x, y, z координата өстеріне қатысты қозғалыс мөлшері моменттерінің өзгеруі туралы теореманы береді: нүктенің кез келген өске қатысты қозғалыс мөлшері моментінен уақыт бойынша алынған туынды нүктеге әсер ететін күштің осы өске қатысты моментіне тең.

Қозғалыс мөлшерінің моменті үшін екі сақталу заңы орындалады:

1 Егер әсер ететін күштің бір центрге қатысты моменті нөлге тең болса, онда нүктенің осы центрге қатысты қозғалыс мөлшері моментінің сан шамасы мен бағыты тұрақты болады.

2 Егер әсер ететін күштің бір өске қатысты моменті нөлге тең болса, онда нүктенің осы өске қатысты қозғалыс мөлшерінің моменті тұрақты болады. Бұл тұжырымды (10) өрнегі береді.

Негізгі әдебиеттер: 4 [IІІ бөлім, 16 тарау, 158-162б], 8 [IІІ бөлім, §§109-111, 116].

Қосымша әдебиеттер: 11 [IІІ бөлім, 4 тарау, §§3,4, 296-297, 306, 308, 312б].

Бақылау сұрақтары:

1. Шекті уақыт аралығындағы күш импульсі.

1. Нүктенің қозғалыс мөлшері мен оның өзгеруі туралы теореманың дифференциалдық және шекті түрлері.

1. Қозғалыс мөлшерінің моменті.

1. Нүктенің центрге және өске қатысты қозғалыс мөлшері моментінің өзгеруі туралы теоремалар.

1. Нүктенің центрге және өске қатысты қозғалыс мөлшері моментінің сақталу заңы.

ДӘРІС-12.Нүкте динамикасының жалпы теоремалары (жалғасы). Нүкте үшін Даламбер принципі.

3.12.1 Күш жұмысы. Қуат. Нүкте орын ауыстырғандағы күш әсерін сипаттау үшін жұмыс ұғымы қолданылады. М нүктесіне әсер ететін 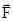күшінің (24 сурет) элементар жұмысы деп

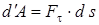, (11)

скаляр шамасын айтады, мұндағы 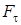- 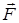күшінің Мt жанама өске проекциясы (немесе 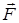күшінің М нүктесінің 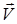жылдамдығы бағытына проекциясы); ds – М нүктесінің элементар орын ауыстыру модулі.

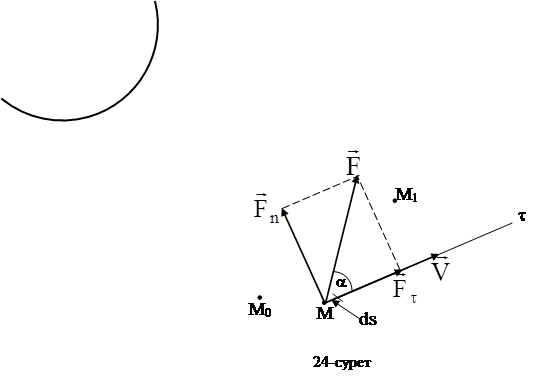
(a - және Мt арасындағы бұрыш) болғандықтан, (11) өрнегінен күштің элементар жұмысының тағы бір өрнегін аламыз:

. (12)

1. Егер a бұрышы сүйір болса (0<a<90⁰), жұмыс оң таңбалы болады. Ал a = 0 болғанда элементар жұмыс .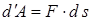

2. Егер a бұрышы доғал болса (90⁰ < a < 180⁰), жұмыс теріс таңбалы болады. Ал a = 180⁰ болғанда элементар жұмыс .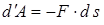

3. Егер a = 90⁰ болса, яғни егер күш векторы жүріп өткен жолға немесе жылдамдыққа перпендикуляр бағытталса, күштің элементар жұмысы нөлге тең болады.

Кинематикадан 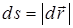екендігі белгілі (бұл жердегі 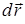- нүктенің элементар орын ауыстыру векторы), сондықтан элементар жұмысты мына түрде жазуға болады:

,

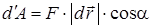бұл 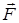және 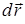векторларының скалярлық көбейтіндісі, яғни

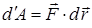. (13)

(13) өрнегін векторлардың проекциялары арқылы да жазуға болады:

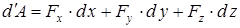, (14)

x, y, z – 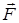күшінің түсу нүктесінің координаталары.

<2 3 456 7 8 >

Дата добавления: 2015-06-17; просмотров: 7780;