Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. 2 страница
 . (3)
. (3)
Бас вектордың шамасы (модулі) мына өрнекпен анықталады:
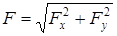 , (4)
, (4)
ал бағыты бағыттаушы косинустардың көмегімен анықталады:
 ,
, 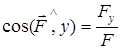 . (5)
. (5)
Бұл жағдайда О нүктесіне қатысты бас момент барлық күштердің О нүктесіне қатысты моменттерінің алгебралық қосындысы болады:
 . (6)
. (6)
Егер денеге күштермен қатар қос күштер әсер етсе, олардың моменттері жүйенің бас моментіне қосылады.
1.3.3 Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттары. Күштердің кез келген жазық жүйесі тепе-теңдікте болу үшін оның бас векторы мен кез келген бір О нүктесіне қатысты алынған бас моментінің нөлге тең болуы қажет және жеткілікті, яғни
 .
.
Бұл шарттар аналитикалық түрде скалярлық тепе-теңдік шарттары түрінде жазылады.
Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының бірінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің екі координата өсіне (х пен у) проекцияларының қосындысы мен күштер жазықтығындағы кез келген О нүктеге қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
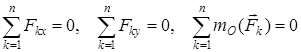 (7)
(7)
Жазықтықтағы кез келген күштер жүйесінің аналитикалық тепе-теңдік шарттарын бұдан басқа тағы екі түрде жазуға болады.
Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының екінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің күштер жазықтығындағы бір өске (х) проекцияларының қосындысы мен осы өске перпендикуляр түзуде жатпайтын екі нүктеге (А және В) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
 . (8)
. (8)
Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттарының үшінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін бір түзудің бойында жатпайтын үш нүктеге (А, В және С) қатысты алынған барлық күштердің моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
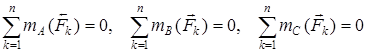 . (9)
. (9)
Есеп шығарған кезде, егер күштің нүктеге қатысты иінін анықтау қиын болса, онда күшті құраушыларға жіктеп, Вариньон теоремасын қолдануға болады.
1.3.4 Таралған күштер. Қатаң бекітпе. Денелер жүйесінің тепе-теңдігі. Дененің бір нүктесіне түскен күш қадалған күш деп аталады. Бұдан басқа түзу бойымен, жазықтыққа немесе көлемге әсер ететін күштер де бар. Мұндай күштер таралған күштер деп аталады.
 Жазықтықтағы кез келген күштер жүйесі үшін түзу сызық бойымен таралған күштерді қарастырамыз.
Жазықтықтағы кез келген күштер жүйесі үшін түзу сызық бойымен таралған күштерді қарастырамыз.
Біркелкі таралған күш (жүк) депәсері түзу сызық бойымен біркелкі таралған күшті айтады (7- сурет).
Біркелкі таралған күштің таралу қарқындылығы,
яғни жүктелген кесіндінің ұзындық бірлігіне келетін күш беріледі. Бұл жағдайда біркелкі таралған күш тең әсерлі 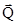 күшпен алмастырылады. Оның модулі
күшпен алмастырылады. Оның модулі
 , (10)
, (10)
ал түсу нүктесі жүктелген кесіндінің ортасы болады (7- сурет).
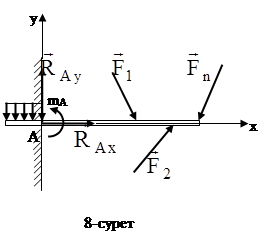 Қатаң бекітілген дене (қатаң бекітпе). Кейбір жағдайларда дененің бір ұшы қабырғаға немесе еденге қазықша қадай бекітіледі.
Қатаң бекітілген дене (қатаң бекітпе). Кейбір жағдайларда дененің бір ұшы қабырғаға немесе еденге қазықша қадай бекітіледі.
Бұл бекітуді қатаң бекітпе (қадалған ұш) деп атаймыз. Жылжымайтын (қозғалмайтын) топсаға қарағанда байланыстың мұндай түрі дене қозғалысына тағы да бір кедергі жасайды. Ол – дененің айналуының шектелуі. Бұл жағдайда дененің көлденең қимасында оның бекітілген ұшынан таралған күштер жүйесі (реакциялар) әсер етеді. Бұл күштерді қиманың А нүктеcіне келтірілген деп санап, оларды осы центрге
түсірілген  және
және  құраушылары бар бір күшпен және моменті
құраушылары бар бір күшпен және моменті  - қатаң бекітпенің реактивті моменті болатын бір қос күшпен алмастыруға болады (8- сурет).
- қатаң бекітпенің реактивті моменті болатын бір қос күшпен алмастыруға болады (8- сурет).
Өзара байланыстағы (құрама құрылманың) денелер жүйесінің тепе-теңдігін қарастырғанда жүйені жеке денелерге бөліп, денелердің әрқайсысының тепе-теңдігін бөлек зерттеу қажет. Бөлініп тасталғанденелердің әсері реакция күштерімен (ішкі күштермен) алмастырылады. Төртінші аксиомаға сәйкес, бөлінген денелердің бір біріне әсер ететін реакция күштерінің шамалары тең, бағыттары қарама қарсы бағытталады.
Негізгі әдебиеттер: 4 [I бөлім, 6 тарау, 39-51б], 8 [I бөлім, §§14-24, 46-66б].
Қосымша әдебиеттер: 11 [I бөлім, 5 тарау, §§1-6, 48-60б].
Бақылау сұрақтары:
Кез келген жазық күштер жүйесінің анықтамасы.
Нүктеге қатысты күш моменті мен қос күш моментінің алгебралық мәні.
Күштер жүйесінің бас векторы мен бас моменті.
Жазық күштер жүйесінің аналитикалық тепе-теңдік шарттары, олардың түрлері.
ДӘРІС-4.Дененің ауырлық центрі.
1. Параллель күштер центрі. 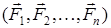 параллель күштер жүйесін қарастырайық. Олардың тең әсерлі күші:
параллель күштер жүйесін қарастырайық. Олардың тең әсерлі күші:
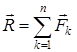 . (1)
. (1)
Енді осы күштерді олардың түсу нүктесі төңірегінде бір бағытта және бірдей бұрышқа бұрайық. Алынған күштер жүйесі модульдері мен түсу нүктелері өзгермеген параллель күштер жүйесі болады. Осындай күштер жүйесінің әрқайсысының тең әсерлі күшінің модулі бұрынғыдай, ал бағыты әртүрлі болады. Күштер жүйесін кез келген жаққа бұрғанда тең әсерлі күштің әсер ету сызығы бір С нүктесі арқылы өтетін болады. Осы нүкте параллель күштер центрі деп аталады.
Вариньон теоремасын қолданып осы нүктенің радиус-векторын алуға болады. Дәріс оқығанда қарастырылатын біраз түрлендірулерден кейін параллель күштер центрінің радиус-векторын анықтайтын өрнек алынады:
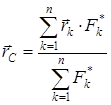 , (2)
, (2)
мұндағы  -
-  күшінің түсу нүктесінің радиус-векторы , ал
күшінің түсу нүктесінің радиус-векторы , ал 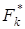 бағытына сәйкес не
бағытына сәйкес не 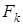 -ға, не
-ға, не  -ға тең.
-ға тең.
1.4.2. Қатты дененің ауырлық центрі. Жер бетіне жақын орналасқан дененің әр нүктесіне жердің центріне бағытталған ауырлық күштері әсер етеді. Егер дене өлшемдері жер өлшемдерінен әлдеқайда кіші болса, онда бұл күштерді барлығының шамалары тұрақты және бір біріне параллель деп есептеуге болады.
Берілген дененің нүктелеріне әсер ететін 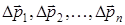 ауырлық күштердің тең әсерлісі
ауырлық күштердің тең әсерлісі 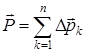 , параллель күштер жүйесінің тең әсерлі күші ретінде, әрқашан бір нүктеден өтеді. Осы күштің модулі дененің салмағы болады. Дененің ауырлық центрі деп оның барлық нүктелерінің ауырлық күштерін құратын параллель күштер жүйесінің центрін атайды. Дененің ауырлық центрінің радиус-векторын (2) өрнегіне сәйкес мына формуламен санауға болады:
, параллель күштер жүйесінің тең әсерлі күші ретінде, әрқашан бір нүктеден өтеді. Осы күштің модулі дененің салмағы болады. Дененің ауырлық центрі деп оның барлық нүктелерінің ауырлық күштерін құратын параллель күштер жүйесінің центрін атайды. Дененің ауырлық центрінің радиус-векторын (2) өрнегіне сәйкес мына формуламен санауға болады:
 . (3)
. (3)
Егер денені жеке бөлшектерге бөлу мүмкін болмаса, онда көлемнің ауырлық центрінің радиус-векторын мына өрнекпен санауға болады:
 , (4)
, (4)
мұндағы g - дененің меншікті салмағы.
Біртекті денелердің меншікті салмағы тұрақты шама, сондықтан (4) өрнегінің алымы мен бөліміндегі g-ны интеграл таңбасының алдына шығарып, қысқартуға болады. Сонымен қатар, бөлімде тұрған интеграл дененің көлеміне тең. Демек, біртекті көлемнің ауырлық центрінің радиус-векторын мына өрнекпен анықталады:
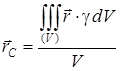 . (5)
. (5)
Осы сияқты өрнектерді біртекті жазық дене мен сызық үшін де жазуға болады.
1. Ауырлық центрдің координаталарын анықтау әдістері. Көлемнің, жазық дене немесе сызықтың ауырлық центрінің координаталарын анықтау интегралдық есептеуді талап етеді. Іс жүзінде ауырлық центрінің орны алдын ала белгілі бірнеше денеден тұратын денелерді жиі кездестіруге болады. Осындай денелердің ауырлық центрінің орнын интегралдық есептеусіз, белгілі бір әдістермен анықтауға болады.
1. Симметрия әдісі. Бұл әдіс біртекті дененің симметрия жазықтығы, симметрия өсі немесе симметрия центрі бар болған кезде қолданылады. Мұндай дененің ауырлық центрі симметрия жазықтығында, не симметрия өсінде, не симметрия центрінде жатады.
1. Бөлшектеу әдісі. Егер берілген дененің пішіні күрделі болса, онда оны ауырлық центрлері оңай табылатын бірнеше бөлшекке бөлеміз. Бөлшектердің ауырлық центрлерін жеке-жеке тауып алғаннан соң біртіндеп дененің ауырлық центрін табамыз.
1. Теріс массалар әдісі. Бұл әдісті қуысты денелерге қолданады. Оны бөлшектеу әдісінің бір түрі деуге болады. Бұл әдісте қуыстарды теріс таңбалы көлемдер, аудандар деп есептейді.
1. Кейбір біртекті денелердің ауырлық центрі. Күрделі денелердің ауырлық центрінің орнын бөлшектеу немесе теріс массалар әдістерімен анықтау үшін күрделі дене бөлінетін қарапайым денелердің ауырлық центрлерін таба білу керек. Осындай біртекті денелерді қарастырайық.
 Үшбұрыш ауданының ауырлық центрі. Біртекті үшбұрыш ауданының ауырлық центрі (С нүктесі) үшбұрыштың медианаларының қиылысу нүктесінде жатады(8-сурет).Олай болса
Үшбұрыш ауданының ауырлық центрі. Біртекті үшбұрыш ауданының ауырлық центрі (С нүктесі) үшбұрыштың медианаларының қиылысу нүктесінде жатады(8-сурет).Олай болса
 .
.
 Шеңбер доғасының ауырлық центрі. Центрі О нүктесіндегі радиусы R шеңбердің АВ доғасын қарастырайық. Доғаның орталық бұрышы АОВ = 2a (10- сурет). Егер Ох өсін симметрия өсі етіп алсақ, ауырлық центрі осы өстің бойында жатады. Доғаның біртекті сызық екенін ескерсек, оның ауырлық центрінің хС координатасын (5) өрнегінің көмегімен табамыз:
Шеңбер доғасының ауырлық центрі. Центрі О нүктесіндегі радиусы R шеңбердің АВ доғасын қарастырайық. Доғаның орталық бұрышы АОВ = 2a (10- сурет). Егер Ох өсін симметрия өсі етіп алсақ, ауырлық центрі осы өстің бойында жатады. Доғаның біртекті сызық екенін ескерсек, оның ауырлық центрінің хС координатасын (5) өрнегінің көмегімен табамыз:
 . (6)
. (6)
Біраз түрлендірулерден соң радиусы R орталық бұрышы 2a біртекті шеңбер доғасының ауырлық центрінің координа-тасын төмендегі түрде аламыз
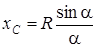 . (7)
. (7)
Дөңгелек сектор ауданының ауырлық центрі. Радиусы R орталық бұрышы 2a дөңгелек сектор ауданының ауырлық центрі Ох симметрия өсінде жатады (11-сурет). ОАВ секторының ауданын О нүктесінен жүргізілген радиустармен n секторға ойша бөлеміз.
Шеңбер доғасының ауырлық центрінің (7) өрнегін қолданып радиусы R орталық бұрышы 2a біртекті дөңгелек сектор ауданының ауырлық центрінің координатасының өрнегін алуға болады:
 . (8)
. (8)
Негізгі әдебиеттер: 4 [I бөлім, 8 тарау, 60-68б], 8 [I бөлім, §§53-57, 129-137б].
Қосымша әдебиеттер: 11 [I бөлім, 8 тарау, §§1-3, 93-102б].
Бақылау сұрақтары:
Параллель күштер жүйесін тең әсерлі күшке келтіру.
Параллель күштер центрі; оның радиус-векторы мен координаталары.
Қатты дененің ауырлық центрі; көлемнің, ауданның және сызықтың ауырлық центрі.
Ауырлық центрді анықтау әдістері.
Кейбір біртекті денелердің ауырлық центрі.
2-модуль «Кинематика»
ДӘРІС-5.Кинематикаға кіріспе. Нүкте кинематикасы.
2.5.1 Кинематикаға кіріспе. Кинематика деп материялық нүктенің немесе дененің қозғалуының тек геометриялық қасиеттерін зерттейтін теориялық механиканың бөлімін айтады. Сол себептен кинематикада күштер мен массаларды қарастырмайды.
Кинематика мәшине және тетіктер қозғалыстарын зертеуде, динамикада, дене, газ, сұйық орталардың қозғалыстарын зерттегенде қолданылады.
Дененің, нүктенің қозғалысын қарастыру үшін санақ жүйесін таңдап алу қажет. Егер кез келген уақытта нүктенің, дененің координаталары өзгеріп отырса, дене санақ жүйесінде қозғалыста болады.
Кинематикада нүктенің жолын, жылдамдығын, үдеуін уақытқа тәуелді функция деп қарастырады. Оларды кинематикалық сипаттамалар дейміз.
Кеңістіктегі нүктенің санақ жүйесіндегі орнының кез келген уақытта белгілі болуын нүкте қозғалысын "кинематикаша анықтау" деп айтамыз.
Дененің қозғалыс заңы белгілі болған жағдайда, оның кинематикалық сипаттамаларын (жылдамдық, үдеу,...) анықтау кинематиканың негізгі мәселесі болып табылады.
2.5.2 Нүкте қозғалысын анықтау әдістері
1 Табиғи әдіс. Кеңістіктегі нүктенің қозғалыс жолын траектория деп атаймыз.
Табиғи әдісті нүктенің траекториясы алдын ала белгілі болған жағдайда пайдаланған жөн.
Егер кеңістікте қозғалатын 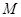 нүктенің траекториясы, О бастапқы нүктесі, қозғалудың оң бағыты,
нүктенің траекториясы, О бастапқы нүктесі, қозғалудың оң бағыты, 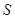 доғалық координатасы берілсе, нүктенің қозғалыс заңы табиғи әдіспен берілген дейміз. Нүкте қозғалғанда оның траекториясының бойымен алынатын қашықтығы,
доғалық координатасы берілсе, нүктенің қозғалыс заңы табиғи әдіспен берілген дейміз. Нүкте қозғалғанда оның траекториясының бойымен алынатын қашықтығы, 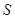 доғалық координатасы
доғалық координатасы  уақыттың функциясы болады:
уақыттың функциясы болады:
 . (1)
. (1)
(1) - нүктенің қозғалыс заңы деп аталады.
2. Координаттық әдіс.  декарт координата жүйесіне қатысты
декарт координата жүйесіне қатысты 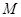 нүктенің орны
нүктенің орны 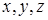 координаттармен анықталады. Нүкте қозғалғанда уақытқа байланысты нүкте координаттары да өзгеріп отырады, яғни уақытқа тәуелді функциялар болады
координаттармен анықталады. Нүкте қозғалғанда уақытқа байланысты нүкте координаттары да өзгеріп отырады, яғни уақытқа тәуелді функциялар болады

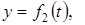
 . (2)
. (2)
Бұл теңдеулерді тік бұрышты декарт координаталарындағы нүкте қозғалысының теңдеулері немесе нүктенің қозғалыс заңдары деп атаймыз.
Траекторияны координаталық түрде жазу үшін нүкте қозғалысының (2) теңдеулерінен  уақытты жою керек.
уақытты жою керек.
3. Векторлық әдіс. Нүктенің кез келген уақыттағы орнын  бас нүктеден шыққан
бас нүктеден шыққан 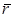 радиус-вектормен анықтауға болады. Нүкте кеңістікте қозғалғанда
радиус-вектормен анықтауға болады. Нүкте кеңістікте қозғалғанда  уақыттың өзгеруіне сәйкес радиус-вектордың модулі және бағыты өзгереді, яғни
уақыттың өзгеруіне сәйкес радиус-вектордың модулі және бағыты өзгереді, яғни 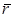 уақытқа тәуелді функция болады:
уақытқа тәуелді функция болады:
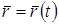 . (3)
. (3)
Бұл теңдеу нүктенің векторлық түрдегі қозғалыс заңын береді.
Радиус-вектордың ұшының кеңістіктегі геометриялық орындарын вектордың годографы дейді. Радиус-вектордың годографы  нүктесінің траекториясын анықтайды.
нүктесінің траекториясын анықтайды.
2.5.3 Нүктенің жылдамдығы мен үдеуі.
9. Векторлық әдіс.
Нүктенің t уақыттағы орны  радиус-векторымен, ал
радиус-векторымен, ал 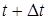 уақыттағы орны
уақыттағы орны  радиус-векторымен анықталсын (12- сурет). Осы векторлардың айырмасын
радиус-векторымен анықталсын (12- сурет). Осы векторлардың айырмасын  арқылы белгілейік, яғни
арқылы белгілейік, яғни
 . (4)
. (4)
Бұл вектор нүктенің элементар  уақыттағы элементар орын ауыстыруы деп аталады.
уақыттағы элементар орын ауыстыруы деп аталады.
Элементар Δ 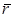 орын ауыстыру векторының элементар
орын ауыстыру векторының элементар 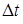 уақытқа қатынасы нүктенің орташа жылдамдығы деп аталады:
уақытқа қатынасы нүктенің орташа жылдамдығы деп аталады:
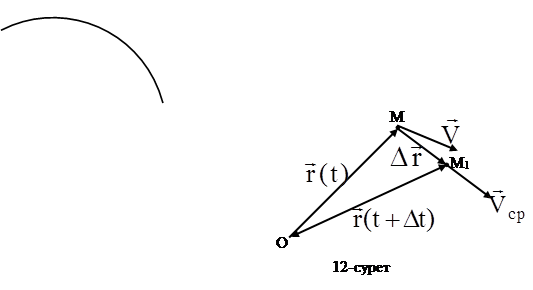
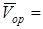
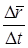 (5)
(5)
Орташа жылдамдықвекторы Δ 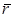 векторы сияқты бағытталады.
векторы сияқты бағытталады.
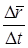 қатынасының
қатынасының 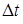 нөлге ұмтылғандағы шегі нүкте жылдамдығы деп аталады, яғни
нөлге ұмтылғандағы шегі нүкте жылдамдығы деп аталады, яғни
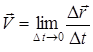 . (6)
. (6)
Демек, нүкте жылдамдығының векторы оның радиус-векторынан уақыт бойынша алынған бірінші туындыға тең екен:
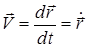 . (7)
. (7)
Жылдамдық векторы нүкте траекториясына жанама бойымен бағытталады (12-сурет).
Дәл осындай талдау жасап 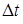 уақыттағы нүктенің орташа үдеуінің:
уақыттағы нүктенің орташа үдеуінің:

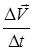 (8)
(8)
және берілген уақыттағы нүкте үдеуінің өрнектерін аламыз:
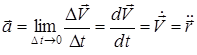 . (9)
. (9)
Демек, нүкте үдеуінің векторы оның жылдамдығының векторынан уақыт бойынша алынған бірінші туындыға немесе радиус-векторынан уақыт бойынша алынған екінші туындыға тең екен.
Нүкте үдеуінің векторы әқашан нүкте траекториясының ойыс жағына қарай бағытталады.
3 Координаталық әдіс. Нүкте қозғалысы координаталық әдіспен берілсе оның радиус-векторын декарттық координата жүйесінің тұрақты  вектолары арқылы жазуға болады:
вектолары арқылы жазуға болады: 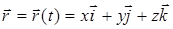 . (7) өрнекті ескере отырып нүктенің жылдамдық векторының декарттық координата өстеріне проекцияларын аламыз:
. (7) өрнекті ескере отырып нүктенің жылдамдық векторының декарттық координата өстеріне проекцияларын аламыз:
 . (10)
. (10)
Нүкте жылдамдығының сан шамасы
 (11)
(11)
өрнегімен, ал бағыты мына бағыттаушы косинустармен анықталады:
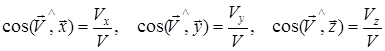 (12)
(12)
Дәл осылай нүкте үдеуінің декарттық координата өстеріне проекцияларын:
 , (13)
, (13)
нүкте үдеуінің сан шамасын:
 (14)
(14)
және үдеу векторының бағыттаушы косинустарын аламыз:
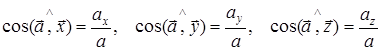 . (15)
. (15)
4 Табиғи әдіс. Бұл әдіспен берілген нүкте үшін жылдамдықтың жалпы анықтамасына сәйкес түрлендірулер жасағаннан кейін, қозғалысы табиғи әдіспен берілген нүкте жылдамдығы векторының өрнегін аламыз:
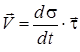 . (16)
. (16)
Нүкте жылдамдығы векторының жанама өске проекциясын анықтайтын  белгілеу ендірсек, онда жылдамдық векторы былай өрнектеледі:
белгілеу ендірсек, онда жылдамдық векторы былай өрнектеледі:
 . (17)
. (17)
Егер  болса жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай ал
болса жылдамдық векторы нүкте траекториясына жанама бойынша қозғалыстың оң бағытына қарай ал  болса – теріс бағытына қарай бағытталады. Жылдамдықтың сан шамасы:
болса – теріс бағытына қарай бағытталады. Жылдамдықтың сан шамасы:
Дата добавления: 2015-06-17; просмотров: 3708;
