Теорема. Нүктенің абсолют үдеуі оның тасымал, салыстырмалы және Кориолис үлеулерінің геометриялық қосындысына тең. 3 страница
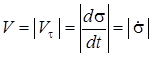 . (18)
. (18)
Қозғалысы табиғи әдіспен берілген нүкте үдеуінің векторын анықтау үшін табиғи үшжақтық ұғымын ендіреміз (13а сурет). Бұл санақ жүйесінің ерекшілігі – оның бас нүктесі ретінде қозғалыстағы нүкте алынады да, жүйе сол нүктемен бірге қозғалады. Нүкте траекториясына жанама өсті 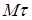 деп, бас нормаль өсті
деп, бас нормаль өсті  деп белгілейміз. Мtn жазықтығына нормаль өсті
деп белгілейміз. Мtn жазықтығына нормаль өсті 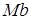 деп белгілеп, бинормаль өсі деп атаймыз.
деп белгілеп, бинормаль өсі деп атаймыз.
Нүкте үдеуін анықтау үшін қозғалыс барысында 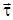 векторының бағытының өзгеретінін ескере отырып, оның жылдамдығы векторынан (17) бірінші туынды аламыз:
векторының бағытының өзгеретінін ескере отырып, оның жылдамдығы векторынан (17) бірінші туынды аламыз:
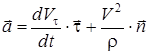 . (19)
. (19)

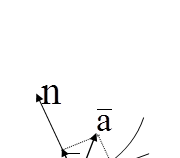
а)
13-сурет
(19) өрнегінен нүкте үдеуі векторының жанасушы жазықтықта жататынын және екі құраушыдан (жанама және нормаль) тұратынын көреміз. Үдеудің жанама құраушысы траекторияға жанама бойынша, ал нормаль құраушысы – бас нормаль бойымен траекторияның ойыс жағына қарай бағытталған (13ә сурет). Сонымен, нүктенің толық үдеуінің векторы үдеудің жанама және нормаль құраушыларының геометриялық қосындысына тең екен:
 . (20)
. (20)
Үдеудің жанама өске проекциясы нүктенің жанама үдеуі деп:
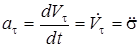 , (21)
, (21)
ал бас нормальға проекциясы нүктенің нормальүдеуі деп аталады:
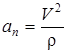 , (22)
, (22)
мұндағы r – траекторияның қисықтық радиусы.
Нүктенің толық үдеуінің сан шамасы (модулі) Пифагор теоремасымен анықталады:
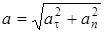 . (23)
. (23)
2.5.4 Нүкте қозғалысының кейбір дербес жағдайлары. Нүкте қозғалысының бірнеше дербес жағдайларын қарастырып, оның негізгі кинематикалық сипаттамаларын анықтайық..
1. Нүктенің түзу сызықты қозғалысы.Түзу сызықты қозғалыстағы нүктенің қисықтық радиусы шексіздікке тең. Мұндай қозғалыста (22) өрнегінен нормаль үдеудің нөлге айналатынын, ал толық үдеудің жанама үдеуге тең екенін көреміз:
 .
.
Бұл жағдайда жылдамдықтың тек шамасы ғана өзгереді, демек жанама үдеужылдамдық шамасының өзгеруін сипаттайды.
Бірқалыпты қозғалыс.Қозғалыс барысында жылдамдық шамасы әрқашан тұрақты болатын қозғалысбірқалыпты қозғалыс деп аталады. Мұндай қозғалыс кезінде (21) өрнегіне сәйкес жанама үдеунөлге тең, ал толық үдеу тек нормаль үдеуге тең болады:
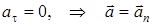
Мұндай қозғалыста жылдамдықтың тек бағыты ғана өзгереді, сондықтан нормаль үдеужылдамдық бағытының өзгеруін сипаттайды.
Нүктенің бірқалыпты түзу сызықты қозғалысы.Нүкте бір мезгілде бірқалыпты және түзу сызықты қозғалыс жасағандықтан оның жанама және нормаль үдеулері бір мезгілде нөлге айналады. Демек, мұндай қозғалыста нүктенің толық үдеуі де нөлге тең болады:
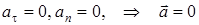 .
.
Бірқалыпты және түзу сызықты қозғалыстағы нүкте жылдамдығының шамасы да, бағыты да тұрақты болады.
Негізгі әдебиеттер: 4 [IІ бөлім, 9 тарау, 69-89б], 8 [IІ бөлім, §§58-68].
Қосымша әдебиеттер: 11 [IІ бөлім, 1 тарау, §§1-5, 103-121б].
Бақылау сұрақтары:
1. Кинематика пәні және оның негізгі ұғымдары.
2. Кинематика мәселелері.
3. Нүкте қозғаласының берілу тәсілдері.
4. Нүктенің жылдамдығы мен үдеуі.
5. Табиғи үшжақтық. нүктенің жанама және нормаль үдеулері.
ДӘРІС-6.Қатты дененің қарапайым қозғалыстары.
2.6Қатты дененің қарапайым қозғалыстары. Абсолют қатты дене деп кез келген екі нүктесінің аралығы өзгермейтін денені атаймыз.
Қатты дене кинематикасында екі мәселе қарастырамыз: дененің қозғалыс заңы берілгенде дененің 1) кинематикалық сипаттамаларын анықтау, 2) әр нүктесінің кинематикалық сипаттамаларын табу.
Ілгерілемелі және тұрақты өсті айнала қозғалыстар дененің қарапайым қозғалыстарына жатады. Күрделі қозғалыстар осындай қозғалыстардың қосындыларынан тұрады.
2.6.1Ілгерілемелі қозғалыс. Дене қозғалғанда денеде белгіленген бір түзу кесінді өзіне өзі параллель болып отырса, дененің қозғалысын ілгерілемелі қозғалыс деп атаймыз.
Теорема. Егер кез келген дене ілгерілемелі қозғалыста болса, онда оның барлық нүктелері бірдей жылдамдықпен, бірдей үдеумен және бірдей траекториямен қозғалады.
Бұдан ілгерілемелі қозғалыс бір нүктенің қозғалысымен анықталатынын байқаймыз.
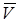 жылдамдықты,
жылдамдықты, 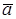 үдеуді ілгерілемелі қозғалыстағы дене жылдамдығы, дене үдеуі деп атаймыз.
үдеуді ілгерілемелі қозғалыстағы дене жылдамдығы, дене үдеуі деп атаймыз.
2.6.2 Дененің тұрақты өсті айнала қозғалуы. Егер дене қозғалғанда оның кез келген екі нүктесі қозғалмайтын (орын ауыстырмайтын) болса, ондай қозғалысты тұрақты өсті айнала қозғалу дейміз. Қозғалмайтын екі А, В нүктелерден өтетін түзуді айналмалы қозғалыстың өсі дейміз.
Аталған А, В нүктелердің аралығы өзгермейтін болғандықтан, АВ өсінде жатқан барлық нүктелер қозғалысқа қатыспайды. Өс бойында жатпайтын нүктелер шеңбер бойымен қозғалады. Шеңберлер өске перпендикуляр жазықтықтарда жатады. Олардың центрлері өстің бойында болады.
Айналмалы қозғалыстағы дененің кез келген уақыттағы орнын табу үшін кеңістікте бір қозғалмайтын (І) және денемен бірге қозғалатын (ІІ) жазықтық аламыз. Бастапқы 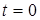 кезде (ІІ) екінші жазықтық қозғалуын бірінші жазықтың орнынан бастаса, кез келген t уақытта (ІІ)-жазықтық j бұрышқа бұрылады. Бұл бұрышты дененің айналу бұрышы деп атаймыз. Айналу бұрышы j радианмен
кезде (ІІ) екінші жазықтық қозғалуын бірінші жазықтың орнынан бастаса, кез келген t уақытта (ІІ)-жазықтық j бұрышқа бұрылады. Бұл бұрышты дененің айналу бұрышы деп атаймыз. Айналу бұрышы j радианмен
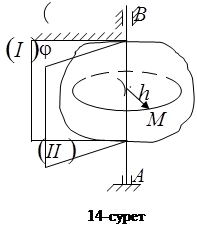 өлшенеді,
өлшенеді, 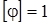 радиан.
радиан.  бұрышы уақытқа тәуелді:
бұрышы уақытқа тәуелді:
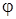 =
= 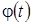 (1)
(1)
(4)-теңдеуді дененің айналу заңы, немесе дененің айналу теңдеуі деп атаймыз.
Айналу бұрышының бірінші туындысын дененің 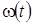 бұрыштық жылдамдығы
бұрыштық жылдамдығы
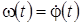 , (2)
, (2)
екінші 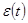 туындысын
туындысын
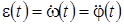 (3)
(3)
бұрыштық үдеуі деп атаймыз.
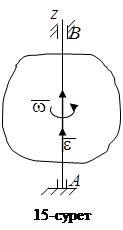
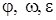 шамаларын айнала қозғалыстың кинематикалық сипаттамалары дейді. Өлшемдері:
шамаларын айнала қозғалыстың кинематикалық сипаттамалары дейді. Өлшемдері:  ,
, 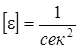 .
.
Бұрыштық жылдамдықтың оң бағыты деп өстің ұшынан қарағанда сағат тілінің айналуына қарсы бағытты айтамыз.
Бұрыштық жылдамдықты вектор 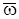 түрінде қарастыруға болады (15-сурет). Ол үшін оны өспен бағыттас етіп алғанда, оның ұшынан дене сағат тіліне қарсы бағытта айналатындай болып көрінуі керек.
түрінде қарастыруға болады (15-сурет). Ол үшін оны өспен бағыттас етіп алғанда, оның ұшынан дене сағат тіліне қарсы бағытта айналатындай болып көрінуі керек.
Бұрыштық үдеуді де вектор 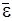 ретінде қарастырсақ, айналу үдемелі болса,
ретінде қарастырсақ, айналу үдемелі болса, 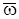 мен
мен 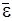 векторлары бағыттас, ал айналу кемімелі болса, қарама -қарсы бағытталған болады.
векторлары бағыттас, ал айналу кемімелі болса, қарама -қарсы бағытталған болады.
2.6.3 Дененің бірқалыпты және бірқалыпты айнымалы қозғалыстары. Егер 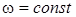 болса, онда айналуды бірқалыпты айналу дейді.
болса, онда айналуды бірқалыпты айналу дейді.
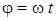 . (4)
. (4)
(4) – қозғалмайтын өске қатысты бірқалыпты айналу заңы. (4) теңдеуінен
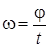 . (5)
. (5)
Техникада көп жағдайда дене бірқалыпты айналғанда бұрыштық жылдамдықтың орнына 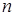 минуттік айналым саны қарастырылады.
минуттік айналым саны қарастырылады. 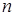 мен
мен 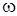 -ның байланысы оңай анықталады:
-ның байланысы оңай анықталады:
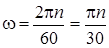 . (6)
. (6)
Егерде 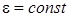 болса, онда айналуды бірқалыпты анымалы айналу дейміз. Бірқалыпты айнымалы айналу заңы
болса, онда айналуды бірқалыпты анымалы айналу дейміз. Бірқалыпты айнымалы айналу заңы
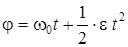 (7)
(7)
Түрінде жазылады.
2.6.4 Тұрақты өсті айнала қозғалатын дене нүктелерінің жылдамдықтары мен үдеулері.
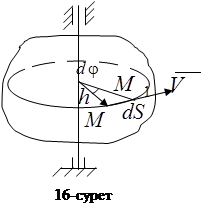 Тұрақты өстен h аралықтағы кез келген М нүктенің қозғалысын қарастырайық (16-сурет). Ол дененің айнала қозғалысында радиусы h, өске перпендикуляр шеңбермен қозғалады. Элементар
Тұрақты өстен h аралықтағы кез келген М нүктенің қозғалысын қарастырайық (16-сурет). Ол дененің айнала қозғалысында радиусы h, өске перпендикуляр шеңбермен қозғалады. Элементар  уақыт аралығында дене
уақыт аралығында дене 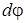 бұрышқа айналса, нүкте шеңбер бойымен
бұрышқа айналса, нүкте шеңбер бойымен 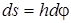 аралыққа көшеді.
аралыққа көшеді.
Онда нүкте жылдамдығы
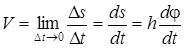
болады, яғни
 . (8)
. (8)
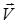 жылдамдық М нүктеде шеңбердің жанамасымен бағыттас болады.
жылдамдық М нүктеде шеңбердің жанамасымен бағыттас болады.
 Нүктенің үдеуін табу үшін белгілі өрнектерді пайдаланамыз:
Нүктенің үдеуін табу үшін белгілі өрнектерді пайдаланамыз:
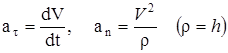 . (8)-ді еске алсақ
. (8)-ді еске алсақ 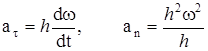 , яғни
, яғни
 . (9)
. (9)
Жанама үдеу 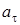 траектория жанамасының бойымен бағытталады,
траектория жанамасының бойымен бағытталады, 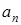 нормальдық үдеу радиус бойымен центрге бағытталады (17-сурет).
нормальдық үдеу радиус бойымен центрге бағытталады (17-сурет).
Толық үдеу модулі
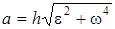 . (10)
. (10)
Толық үдеу векторы радиуспен  бұрышын жасайды:
бұрышын жасайды:
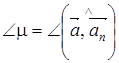 ;
; 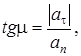 (11)
(11)
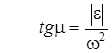 (11/)
(11/)
Негізгі әдебиеттер: 4 [IІ бөлім, 10 тарау, 90-100б], 8 [IІ бөлім, §§73-76, 170-179б].
Қосымша әдебиеттер: 11 [IІ бөлім, 2 тарау, §§2,3, 135-144б].
Бақылау сұрақтары:
1. Қатты дененің ілгерілемелі қозғалысы.
2. Қатты дененің тұрақты өсті айнала қозғалысы.
3. Дененің бұрыштық жылдамдығы мен бұрыштық үдеуі.
4. Айналмалы қозғалыстағы дене нүктесінің жылдамдығы мен үдеуі.
ДӘРІС-7.Қатты дененің жазық-параллель қозғалысы.
2.7.1 Қатты дененің жазық-паралель қозғалысының теңдеулері
Егер дененің барлық нүктелері қозғалмайтын жазықтыққа параллель көшіп отырса, онда дененің қозғалысын жазық-параллель қозғалыс деп атаймыз. Жазық-параллель қозғалыста денедегі 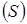 қима қозғалмайтын жазықтыққа параллель қозғалып отырады. Дененің қозғалысын анықтау үшін
қима қозғалмайтын жазықтыққа параллель қозғалып отырады. Дененің қозғалысын анықтау үшін 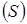 қиманың қозғалысын білген жеткілікті.
қиманың қозғалысын білген жеткілікті. 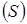 қиманың әр сәттегі өз жазықтығындағы орны оның кез келген
қиманың әр сәттегі өз жазықтығындағы орны оның кез келген 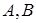 нүктелерімен немесе
нүктелерімен немесе 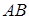 кесіндісімен анықталады.
кесіндісімен анықталады.
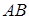 кесіндінің орны кез келген уақытта
кесіндінің орны кез келген уақытта 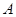 нүктесінің орнымен, яғни
нүктесінің орнымен, яғни 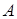 нүктесінің
нүктесінің 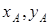 координаталарымен және
координаталарымен және 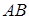 кесіндінің
кесіндінің 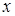 өсімен құратын
өсімен құратын 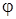 бұрышымен анықталады (2-сурет). Аталған
бұрышымен анықталады (2-сурет). Аталған 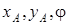 шамалар уақытқа байланысты өзгеріп отырады. Демек, қатты дененің жазық-паралель қозғалысы
шамалар уақытқа байланысты өзгеріп отырады. Демек, қатты дененің жазық-паралель қозғалысы
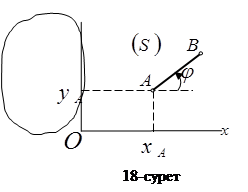
 ,
, 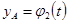 ,
, 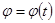 (1)
(1)
теңдеулерімен беріледі. Бұл теңдеулерді дененің жазық-паралель қозғалысының теңдеулері немесе
қозғалыс заңы деп атаймыз. Денедегі кез келген қозғалысы белгілі 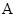 нүктесін полюс деп атаймыз.
нүктесін полюс деп атаймыз.
Демек, қатты дененің жазық-паралель қозғалысы оның ілгерілемелі қозғалысы мен полюс нүктесін айнала қозғалысынан құралады.
Ілгерілемелі қозғалыста нүктелер полюспен бірдей қозғалады. Негізгі кинематикалық сипаттамалар: 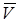 -жылдамдық,
-жылдамдық, 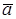 -үдеу,
-үдеу, 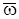 -бұрыштың жылдамдық,
-бұрыштың жылдамдық, 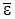 -бұрыштық үдеу болады. Олар дене қозғалысының (1)-ші теңдеулерінен табылады.
-бұрыштық үдеу болады. Олар дене қозғалысының (1)-ші теңдеулерінен табылады.
2.7.2 Жазық қозғалыстағы дене нүктелерінің жылдамдықтарын табу.
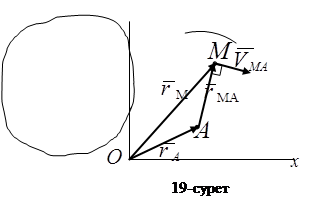 Жазық-параллель қозғалыстағы қатты дененің кез келген М нүктесінің жылдамдығын табайық (19-сурет).
Жазық-параллель қозғалыстағы қатты дененің кез келген М нүктесінің жылдамдығын табайық (19-сурет).
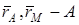 және
және 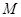 нүктелерінің
нүктелерінің 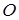 нүктеге қатысты радиус-векторлары.
нүктеге қатысты радиус-векторлары.  векторы М нүктенің
векторы М нүктенің 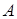 полюсті айнала қозғалуын сипаттайды. Қарастырылатын дене қатты дене болғандықтан
полюсті айнала қозғалуын сипаттайды. Қарастырылатын дене қатты дене болғандықтан  векторының модулі өзгермейді.
векторының модулі өзгермейді.
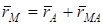 ,
,  екенін еске алсақ,
екенін еске алсақ,
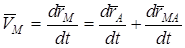 ,
,
мұндағы 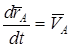 - полюс жылдамдығы,
- полюс жылдамдығы,  -
- 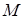 нүктенің дене үйек нүктесін айналғанда алатын жылдамдығы. Демек,
нүктенің дене үйек нүктесін айналғанда алатын жылдамдығы. Демек,
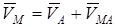 , (2)
, (2)
мұндағы
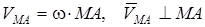 .
.
Сонымен, дененің кез келген М нүктесінің жылдамдығы полюс ретінде алынған дененің басқа А нүктесінің жылдамдығы мен М нүктесінің полюсті денемен бірге айналғанда алатын жылдамдығының геометриялық қосындысына тең.
Теорема: Жазық паралель қозғалыстағы қатты дененің кез келген екі нүктесінің жылдамдықтарының сол нүктелерден өтетін түзуге проекциялары өзара тең.
2.7.3 Нүкте жылдамдығын лездік жылдамдықтар (нүктесі) центрі арқылы табу. Дененің 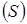 қимасының қозғалысында кез келген уақытта жылдамдығы нөлге тең бір нүкте болады. Ол нүктені айналу центрі немесе жылдамдықтардың лездік центрі деп атаймыз.
қимасының қозғалысында кез келген уақытта жылдамдығы нөлге тең бір нүкте болады. Ол нүктені айналу центрі немесе жылдамдықтардың лездік центрі деп атаймыз.
Ондай нүкте кез келген уақытта бар болады және жалғыз. Оны Р деп белгілейік. Енді 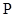 нүктені полюс деп алсақ
нүктені полюс деп алсақ
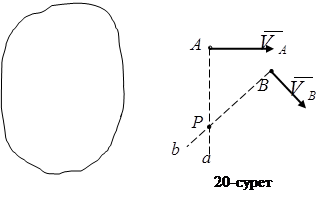
 ,
,
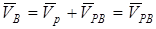 .
.
Демек, 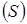 қиманың кез келген нүктесінің жылдамдығы оның
қиманың кез келген нүктесінің жылдамдығы оның  нүктені айнала қозғалудағы жылдамдығына тең:
нүктені айнала қозғалудағы жылдамдығына тең:
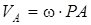
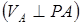 ,
,
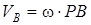
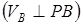 , т.с.с.
, т.с.с.
Онда
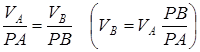 . (3)
. (3)
Яғни, дене нүктелерінің жылдамдықтары олардың лездік жылдамдықтар центріне дейінгі қашықтықтарына пропорционал болады.
Сонымен,
1) Кез келген нүктенің жылдамдығын табу үшін бір нүктенің жылдамдығы (модулі, бағыты) және ізделінді жылдамдықтың бағыты белгілі болуы керек.
2) Лездік жылдамдықтар центрін табу үшін екі нүктенің жылдамдықтарына сол нүктелерде перпендикулярлар құру қажет. Олардың қиылысу нүктесі лездік жылдамдықтар центрін береді (20-сурет).
Лездік жылдамдықтар центрін табудың басқа да жағдайларын келтірейік (21-сурет).
а) Егер жазық-паралель қозғалыста бір цилиндрлік дене екінші қозғалмайтын цилиндрлік дененің бетімен сырғанамай қозғалатын болса, олардың жанасу нүктесі лездік жылдамдықтар центрі болады.
б) Егер А, В нүктелерінің 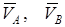 жылдамдықтары өзара параллель және
жылдамдықтары өзара параллель және 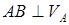 болса, онда лездік жылдамдықтар центрі АВ сызық пен
болса, онда лездік жылдамдықтар центрі АВ сызық пен 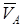 және
және 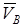 жылдамдықтардың ұштарынан өтетін түзудің қиылысында жатады.
жылдамдықтардың ұштарынан өтетін түзудің қиылысында жатады.
 |
в) Егер 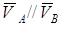 болып,
болып, 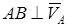 болмаса, онда А, В нүктерінде құрылған перпендикулярлар өзара қиылыспайды, лездік жылдамдықтар центрі мүндай жағдайда болмайды.
болмаса, онда А, В нүктерінде құрылған перпендикулярлар өзара қиылыспайды, лездік жылдамдықтар центрі мүндай жағдайда болмайды. 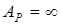 болады. Теорема бойынша
болады. Теорема бойынша 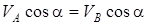 , яғни
, яғни 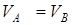 . Демек, мұндай жағдайда қарастырылып жатқан сәтте барлық нүктелердің жылдамдықтары өзара тең болады. Онда дененің қозғалысы лездік ілгерілемелі қозғалыс болады және
. Демек, мұндай жағдайда қарастырылып жатқан сәтте барлық нүктелердің жылдамдықтары өзара тең болады. Онда дененің қозғалысы лездік ілгерілемелі қозғалыс болады және 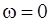 .
.
Негізгі әдебиеттер: 4 [IІ бөлім, 12 тарау, 113-124б], 8 [IІ бөлім, §§77-81].
Қосымша әдебиеттер: 11 [IІ бөлім, 3 тарау, §§1-7, 148-159б].
Бақылау сұрақтары:
1. Қатты дененің жазық-параллель қозғалысы және жазық фигураныың өз жазықтығындағы қозғалысы.
2. Жазық фигура қозғалысын ілгерілемелі және айналмалы қозғалыстарға жіктеу.
3. Фигураның кез келген нүктесінің жылдамдығы.
4. Екі нүкте жылдамдықтарының проекциялары туралы теорема.
5.Жылдамдықтардың лездік центрі және оның көмегімен фигураның кез келген нүктесінің жылдамдығын анықтау.
ДӘРІС-8.Қатты дененің жазық-параллель қозғалысы (жалғасы).
2.8.1 Жазық-параллель қозғалыстағы қатты дене нүктелерінің үдеулерін анықтау. Жазық-параллель қозғалыстағы дене нүктесінің үдеуін табу үшін (2) өрнектен уақыт бойынша туынды аламыз. Сонда
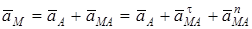 (4)
(4)
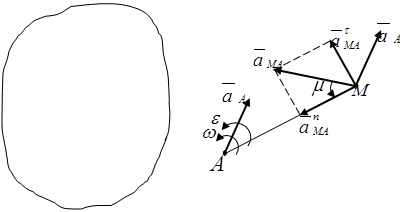 мұндағы
мұндағы
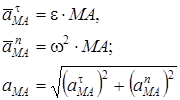 (5)
(5)
Дата добавления: 2015-06-17; просмотров: 7021;
