Есептер шығару үлгілері. Есеп. ОА айналшағы I қозғалмайтын тістегеріш ішінде қозғалатын II қозғалмалы тістегерішті
Есеп. ОА айналшағы I қозғалмайтын тістегеріш ішінде қозғалатын II қозғалмалы тістегерішті қозғалысқа келтіреді (9-сурет). Айналшақтың О нүктесі арқылы өтетін өске қатысты бұрыштық жылдамдығы мен бұрыштық үдеуі 
, 
. II қозғалмалы тістегеріштің В нүктесінің жылдамдығы мен үдеуін және суретте көрсетілген орынға сәйкес оның бұрыштық жылдамдығы мен бұрыштық үдеуін табыңдар, мұндағы ОА=30 см, r=20 см.
Шешімі. Айналшақ О нүктесі арқылы өтетін өс арқылы айналатын болғандықтан, А нүктесінің жылдамдығы
.
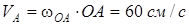векторының бағыты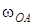 
бағытына сәйкес және ОА векторына перпендикуляр.
Лездік жылдамдықтар центрі P нүктесі жылжымалы және жылжымайтын тістегеріштердің жанасу нүктесінде болады (10-сурет). Ара қашықтықтарды есептейік
.
Белгілі формуладан
.
В нүктесінің жылдамдығы
.
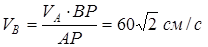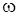векторының бағыты векторының бағытымен анықталады, ал 
векторы ВР кесіндісіне перпендикуляр болады (10-сурет).
В нүктесінің үдеуін табу үшін II қозғалмалы тістегеріштің бұрыштық жылдамдығын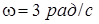 
пайдаланамыз.
ОА айналшақтың бұрыштық жылдамдығы мен бұрыштық үдеуі және II тістегеріштің лездік бұрыштық жылдамдығы арқылы А нүктесінің нормаль және жанама үдеулерін, В нүктесінің А нүктесін айналғандағы центрге тартқыш үдеуін табуға болады:
см/с2,
см/с2,
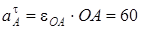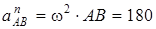см/с2.
Суретте осы үдеулердің бағыттарын кескіндейік: 
векторы А нүктесінен О нүктесіне, 
векторы 
бағытында ОА-ға перпендикуляр,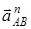 
векторы В нүктесінен А нүктесіне қарай бағытталады (11-сурет). Қозғалмалы тістегеріштің бұрыштық үдеуі
.
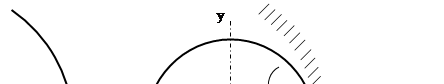
-ның бағыты 
векторының бағытымен бағыттас.
Енді үдеулердің сан мәндерін анықтайық
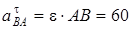см/с2
және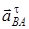 
векторының бағыты, 11-суретте кескінделгендей, 
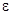бағытына сәйкес 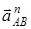үдеуіне перпендикуляр.
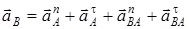
векторлық теңдеуін x және y өстеріне проекцияласақ
60см/с2,
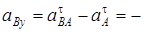120см/с2.
Ендеше В нүктесінің толық үдеуі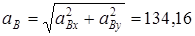 
см/с2.
Негізгі әдебиеттер 6 [№№ 16.11, 16.31, 16.35, 16.39, №№ 18.13, 18.22, 18.23, 18.28]
Қосымша әдебиеттер 13 [стр. 162-178б, 183-197б]
Бақылау сұрақтары:
1. Жазық-параллель қозғалыс туралы түсінік.
2. Жылдамдықтардың проекциялары туралы теорема.
3. Лездік жылдамдықтар центрін табу.
4. Жазық фигура нүктелерінің жылдамдықтарын табу.
5. Жазық фигураың нүктелерінің үдеулерін табу.
6.Дененің бұрыштық үдеуін анықтау.
ТӘЖІРИБЕЛІК САБАҚ-8, 9.Нүктенің күрделі қозғалысы.
Тапсырмалар тізімі:
1 Тасымал, салыстырмалы және абсолют қозғалыстарды ажырату.
2Күрделі қозғалыстағы нүктенің абсолют жылдамдығы мен абсолют үдеуін табу.
Әдістемелік ұсыныстар.Есепті шығару үшін студенттер
58. тасымал, салыстырмалы және абсолют қозғалыстарды ажырата;
59. күрделі қозғалыс кезінде жылдамдықтарды қосу туралы теореманы;
60. нүктенің абсолют үдеуінің қалай анықталатындығын;
61. нүктенің күрделі қозғалысы кезінде үдеулерді қосу туралы теореманы;
62. Кориолис үдеуінің сан мәні мен бағыты қалай анықталатындығын
білуі керек.
Есепті шығару реті
3 Нүктенің берілген қозғалысында тасымал, салыстырмалы және абсолют қозғалыстарды ажырату.
4 Нүктенің қозғалыс түріне сәйкес оның салыстырмалы және тасымал жылдамдықтарының сан мәндері мен бағыттарын анықтау.
5 Нүктенің абсолют үдеуін анықтау.
6 Нүктенің қозғалыс түріне сәйкес оның салыстырмалы, тасымал және Кориолис үдеулерінің сан мәндері мен бағыттарын анықтау.
7Нүктенің абсолют үдеуін анықтау.
Есептер шығару үлгілері.
Есеп №1. Үшбұрыш Oz/ өсін 
бұрыштық үдеуімен үдемелі айналады, осы берілген сәттегі бұрыштық жылдамдығы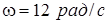 
. АВ қабырғасымен М нүктесі 
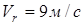жылдамдығымен қозғалады. М нүктесінің абсалют жылдамдығы мен абсолют үдеуін табыңдар, мұндағы МА=2м (12-сурет).
Шешімі. Нүктенің абсолют жылдамдығы салыстырмалы және тасымал жылдамдықтардың геометриялық қосындысына тең
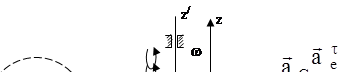
. (1)
Нүктенің АВ бойымен қозғалысы салыстырмалы қозғалыс, ал оның үшбұрышпен бірге Оz/ өсін айналуы тасымал қозғалыс болады.
Тасымал қозғалыстың жылдамдығы
.
Нүктенің абсолют жылдамдығы (1) теңдеудегі жылдамдық векторларын декарт координата өстеріне проекциялау арқылы табылады:
Ендеше
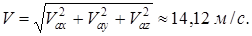
Нүктенің абсолют үдеуі Кориолис теоремасымен анықталады:
.
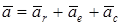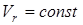болғандықтан, нүктенің салыстырмалы үдеуі
.
Нүктенің тасымал үдеуі екі құраушыдан тұрады
Олардың мәндері төмендегі формулалармен табылады:
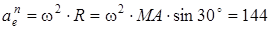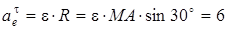м/с2,
м/с2.
Нормаль үдеу векторы тасымал қозғалыста нүкте сызатын шеңбер радиусі бойымен айналу өсіне қарай бағытталған, ал жанама үдеу векторы бағыты бойынша, центрге тартқыш үдеуге перпендикуляр.
Кориолис үдеуінің модулі
.
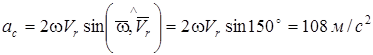векторының бағыты Н.Е. Жуковский ережесі бойынша табылады. Табылған үдеу векторларын координат өстеріне проекцияласақ:
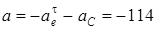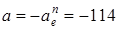м/с2, 
м/с2, 
.
Сонда нүктенің абсолют үдеуінің шамасы
183,66 м/с2.
Негізгі әдебиет 6 [№№, 23.14, 23.27, 23.30, 23.50, 23.29, 23.36, 23.18].
Қосымша әдебиет 13 [201-223б].
Бақылау сұрақтары.
1.Нүктенің күрделі қозғалысы туралы түсінік
2.Нүктенің тасымал, салыстырмалы және абсолют қозғалыстарын анықтау.
3.Нүктенің абсолют жылдамдығын табу.
4.Үдеулерді қосу туралы теорема. Кориолис үдеуінің бағыты мен шамасын анықтау.
Модуль №3 «Динамика»
ТӘЖІРИБЕЛІК САБАҚ-10,11.Материялық нүкте динамикасы. Нүкте динамикасының жалпы теоремалары.
Тапсырма:
1.Динамиканың заңдарын білу.
2.Материялық нүкте қозғалысының дифференциалдық теңдеулерін шешу.
3.Динамиканың тура және кері мәселелерінің шешуі.
4.Нүктенің қозғалыс мөлшерін, шекті уақыт аралығындағы күш импульсін, материялық нүктенің қозғалыс мөлшерінің центрге және өске қатысты моменттерін есептеу.
5.Материялық нүктенің қозғалыс мөлшерінің және қозғалыс мөлшері моментінің өзгеруі туралы теоремаларды есептер шығаруға қолдана білу.
Әдістемелік ұсыныстар.Есепті шығару үшін студенттер
63. динамиканың заңдарын білуі керек;
64. материялық нүкте қозғалысының дифференциалдық теңдеулерін жаза білуі керек;
65. динамиканың тура және кері мәселелерін шеше
66. нүктенің қозғалыс мөлшері, шекті уақыт аралығындағы күш импульсі, материялық нүктенің қозғалыс мөлшерінің центрге және өске қатысты моменттері ұғымдарын;
67. материялық нүктенің қозғалыс мөлшерінің және қозғалыс мөлшері моментінің өзгеруі туралы теоремаларды
білуі керек.
Есепті шығару реті
1.Нүкте динамикасының бірінші мәселесін шешу барысында денеге әсер ететін барлық күштерді, соның ішінде реакция күштерін де көрсетіп, Ньютонның екінші заңын координата өстеріне проекциялап жазып, белгісіз реакция күштерін анықтау.
1.Нүкте динамикасының екінші мәселесін шешу барысында денеге әсер ететін барлық күштерді, соның ішінде реакция күштерін де көрсетіп, Ньютонның екінші заңын координата өстеріне проекциялап жазу.
1. Алынған дифференциалдық теңдеулерді интегралдап, бастапқы шарттардың көмегімен интегралдық тұрақтыларды анықтау.
1. Қажет болған жағдайда, соңғы шарттарды жазып қажетті шамаларды анықтау.
1. Есептің берілгеніне сәйкес, оны қандай теореманың көмегімен шешу керектігін анықтау.
1. Есепті нүктенің қозғалыс мөлшерінің өзгеруі туралы теореманың көмегімен шешкенде, аталған теореманы координата өстеріне проекциялап жазу керек. Мұнда күш импульстерінің проекциялары анықталады.
1.Есепті нүктенің қозғалыс мөлшері моментінің өзгеруі туралы теореманың көмегімен шешкенде, барлық күштердің центрге немесе өске қатысты моменттері анықталады.
Есептер шығару үлгілері.
Есеп №1. Материялық нүкте тыныштық күйден көлбеу жылтыр жазықтық бойымен қозғала бастайды. Нүкте қанша уақытта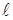 
=20 м жол жүрiп өтедi (g=9,8 м/с2)?
Шешімі. Материялық нүктеге вертикаль төмен бағытталған ауырлық күші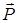 
және көлбеу жазықтықтың реакция күші 
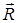әсер етеді. Көлбеу жазықтықтың бойымен қозғалыс бағытымен 
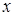өсін бағыттаймыз (13-сурет).
Материялық нүктенің бастапқы орнын өстің бас нүктесі етіп аламыз. Сонда нүкте қозғалысының бастапқы шарттары төмендегі түрде жазылады:
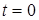болғанда, 
Нүкте қозғалысының 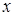өсіне проекцияланған дифференциалдық теңдеуін жазамыз:
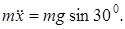
Материялық нүкте қозғалысының дифференциалдық теңдеуін интегралдау үшін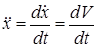 
екенін ескереміз.
Айнымалыларды ажыратып, интегралдасақ
.
Бастапқы шарттың (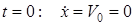 
) көмегімен 
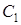интегралдық тұрақтыны табамыз: 
.
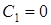Дата добавления: 2015-06-17; просмотров: 3766;