Рідини. Явища в рідинах 5 страница

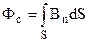. (9.35)

Проекцію вектора індукції на нормаль до поверхні 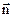запишемо із закону Біо-Савара-Лапаласа (9.4) і принципу суперпозиції (9.8)

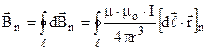. (9.36)

Тоді потік самоіндукції

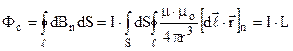. (9.37)

Коефіцієнт пропорційності між потоком самоіндукції і струмом

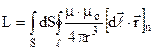(9.38)

залежить тільки від геометричних розмірів контура (S, ℓ, r) і магнітних властивостей середовища (μ, μ_о) і називається індуктивністю контура. За одиницю вимірювання індуктивності в СІ взято Генрі на честь амер. фізика Д.Генрі (1799-1878). Це інтуктивність такої котушки, в якій при зміні струму зі швидкістю 1 А/с виникає е.р.с. самоіндукції 1В.

.

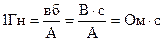Якщо маємо не один виток, а N, то індуктивність буде в N разів більшою, тобто будемо мати справу з потокозчепленням самоіндукції

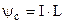. (9.39)

Зважаючи на складність розрахунку поверхневого і криволінійного інтегралів за формулою (9.38), індуктивність розраховують простіше із застосуванням теореми Остроградського-Гауса і закону повного струму.

Приклад 1. Розрахуємо індуктивність соленоїда (див.рис.9.14). Знайдемо потокозчеплення самоіндукції, врахувавши (9.15), (9.25) і (9.39),

.

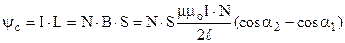Звідки індуктивність 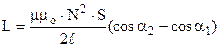. (9.40)

Для довгого соленоїда 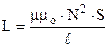. (9.41)

Приклад 2. Розрахуємо індуктивність тороїда, осердя якого показано на рис.9.24. Знайдемо потік індукції через елементарну площу перерізу осердя dS=h∙dr (на рис. заштрихована). Згідно з (9.6) і (9.24) індукція

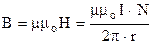, магнітний потік 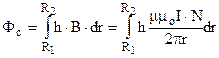, потокозчеплення самоіндукції .

Отже індуктивність тороїда 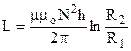. (9.42)

Формули індуктивності (9.41) і (9.42) показують , що вона залежить від геометричних розмірів котушок і магнітних властивостей осердя і не залежить від струму.

Явище самоіндукції заключається у виникненні е.р.с. і індукційного струму в тому ж самому контурі, який є джерелом змінного магнітного поля. По закону Фарадея (9.33) е.р.с. самоіндукції

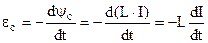(9.43)

прямо пропорційна індуктивності і швидкості зміни струму.

9.13 Зміна струму в котушці при його вмиканні і вимиканні. Фізичний зміст індуктивності

Знайдемо закон зміни струму при підключенні котушки до джерела е.р.с. і її відключенні (рис.9.25). При розімкнутому ключі К струм у колі відсутній. Після замикання ключа в положення 1 в котушці струм наростає. Виникає змінне магнітне поле і е.р.с. самоіндукції. Закон Ома запишеться так , а враховуючи (9.43), маємо 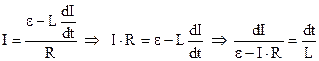. Інтегрування з початковими умовами: при t = 0 I = 0, дає

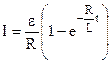(9.44)

зростання струму по експоненті (рис.9.26, криві 1). При 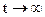струм досягає стаціонарного значення . Після досягнення стаціонарного струму перемикання ключа в положення 2 утворює контур, в якому діє тільки е.р.с. самоіндукції. Закон Ома має вид , або . Інтегрування з початковими умовами:

при , дає

(9.45)

експоненціальний спад струму (рис.9.26, криві 2).

Відношення 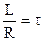називається часом релаксації. Це час, за який струм змінюється в е = 2,718 раз (е - основа натурального логарифму).

Вирази (9.44) і (9.45) показують, що зі збільшенням індуктивності зміна струму в контурі відбувається повільніше (рис.9.26, а і б). Таким чином, індуктивність є міра інертності котушки до зміни в ній електричного струму.

9.14 Енергія та густина енергії магнітного поля

Для збільшення струму в котушці необхідно виконати роботу проти е.р.с. самоіндукції .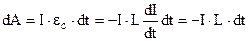

Ця робота перетворюється в енергію магнітного поля 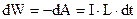. Інтегрування в межах від 0 до І дає

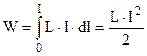. (9.46)

Густина енергії w – це енергія зосереджена в одиниці об’єму простору, де створене магнітне поле

. (9.47)

Знайдемо її на прикладі магнітного поля довгого соленоїда (рис.9.14). Якщо нехтувати крайовими ефектами, то це поле зосереджене всередині котушки, а отже відомий об’єм V = S∙ℓ. Енергію знаходимо по (9.46) з врахуванням (9.41). Одержуємо

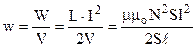. Враховуючи (9.16), маємо

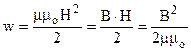. (9.48)