Рідини. Явища в рідинах 2 страница

Висновок. Із прикладів 1-3 видно, що поле зарядженої кулі за її межами таке ж, як і поле точкового заряду, якщо заряд кулі зосередити в її центрі (див. вирази (7.16)-(7.18).

Приклад 4. Поле нескінченної зарядженої осі (циліндра) з лінійною густиною заряду τ (рис.7.15).

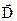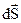Поверхню S виберемо у вигляді циліндра, вісь якого співпадає з зарядженою віссю. Для основ цього циліндра кут між і дорівнює 90^о. Тому потік через основи дорівнює нулю. Для елементів 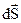бічної поверхні цей кут дорівнює 0^о. Отже можна записати 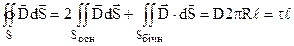Одержуємо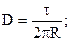 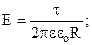(7.22).

Одержаний результат співпадає з (7.12).

Приклад 5. Поле нескінченної зарядженої площини з поверхневою густиною заряду σ (рис.7.16).

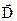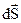Поверхню S вибираємо у вигляді циліндра, основи якого радіусом r паралельні площині. Для бічної поверхні кут між і дорівнює 90^о. Тому потік через бічну поверхню дорівнює нулю. Для елементів 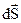основ цей кут дорівнює 0^о. Отже можна записати

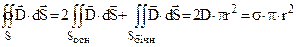Одержуємо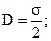 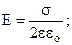(7.23).

Одержали такий же результат, як і в (7.13).

Приклад 6. Поле нескінченних паралельних різнойменно заряджених площин до густини зарядів +σ і -σ.

По принципу суперпозиції . Якщо густини зарядів однакові, то за межами площин 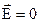(рис.7.17), а між площинами

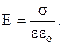(7.24)

7.4 Робота в електростатичному полі. Різниця потенціалів. Потенціал. Циркуляція вектора напруженості електростатичного поля

Нехай в деякому електростатичному полі переміщується заряд q із точки 1 в точку 2 (рис.7.18). На заряд діє сила . Тоді елементарна механічна робота

.

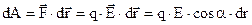Загальна робота знаходиться шляхом інтегрування

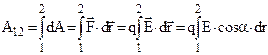, (7.25)

де α – кут між вектором 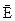і напрямком переміщення .

Для однорідного поля . (7.26)

Покажемо, що робота в електричному полі не залежить від форми шляху, а визначається тільки зарядом q і положеннями початкової і кінцевої точок та напруженістю електричного поля 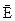. Нехай в однорідному полі напруженістю 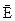переміщується заряд q двома способами (рис.7.19): по прямій 1-2 і по ломаній 1-3-2. Знайдемо роботу електричного поля в обох випадках. .

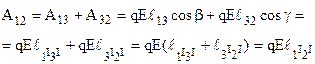Одержали однакову роботу. А це й означає незалежність роботи від форми шляху. Якщо ж поле неоднорідне, то аналогічні міркування виконуються для нескінченно малих відрізків, на яких можна вважати поле однорідним. Загальна робота дорівнює сумі робот на кожному із цих відрізків. Ясно, що якщо на кожному із них робота не залежить від форми шляху, то і сумарна робота не буде залежати від форми шляху.

Якщо в (7.25) віднести роботу до заряду q, то воно уже не буде залежати від величини заряду, а буде визначатись тільки положенням початкової і кінцевої точок та напруженістю поля. Це дає можливість ввести нову енергетичну характеристику поля: потенціал і різницю потенціалів. Із (7.25) одержуємо

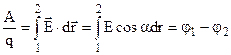(7.27).

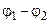- різниця потенціалів, дорівнює роботі, яку виконують сили електростатичного поля при переміщенні одиночного позитивного заряду із точки 1 в точку 2.

Отже робота в електростатичному полі дорівнює добуткові заряду на різницю потенціалів вихідної і кінцевої точок

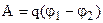. (7.28)

Якщо точку 2 віддалити у нескінченність, де поле відсутнє, одержуємо потенціал

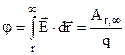(7.29).

Потенціал– це робота сил електричного поля по переміщенню одиничного позитивного заряду із даної точки поля r в нескінченність, де потенціал поля прийнятий за нуль. Потенціал і його різниця вимірюються у вольтах (В).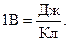

Криволінійний інтеграл по замкнутому контуру 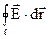називається циркуляцією вектора напруженості. Враховуючи (7.27), видно, що такий інтеграл дорівнює нулю (початкова і кінцева точки переміщення заряду співпадають φ₁ = φ₂). Умова 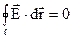є необхідною умовою потенціального характеру поля.

Знайдемо потенціал поля точкового заряду. За означенням

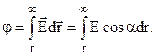Будемо переміщувати пробний заряд q_o по радіальній лінії (рис.7.20). Тоді кут α = 0^о і з врахуванням (7.16) одержуємо

(7.30)

Для потенціалу, як і для напруженості (розділ 7.2), справедливий принцип суперпозиції:

(7.31)

потенціал поля, створеного декількома зарядами, дорівнює алгебраїчній сумі потенціалів, створених у цій точці кожним зарядом. Якщо тіло не точкове, то сума (7.31) переходить в інтеграл.

7.5 Еквіпотенціальні поверхні. Зв’язок між напруженістю і потенціалом електростатичного поля

Геометричне місце точок однакового потенціалу називається еквіпотенціальною поверхнею. Встановимо зв’язок між напруженістю і потенціалом. Нехай маємо дві еквіпотенціальні поверхні з потенціалами φ і φ+dφ (рис.7.21). Перемістимо заряд q із однієї поверхню на другу. Робота для такого переміщення дорівнює:

, або через напруженість

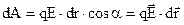
Прирівнюємо праві частини цих рівнянь 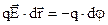, або 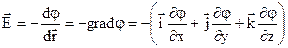. (7.32)

Напруженість дорівнює градієнту потенціалу з протилежним знаком.

Для однорідного поля напруженість дорівнює відношенню різниці потенціалів між двома точками до проекції відстані між ними на напрямок поля 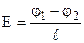. (7.33)

Еквіпотенціальні і силові лінії взаємно перпендикулярні (рис.7.21). Дійсно, при переміщенні заряду по еквіпотенціальній поверхні робота дорівнює нулю ( 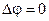). Але на заряд діє сила, і щоб її робота дорівнювала нулю, необхідно, щоб кут між

силою і переміщенням становив 90^о (соs 90^o = 0).

7.6 Електроємність. Конденсатори. З’єднання конденсаторів

Досліди показують, що при зарядженні провідників змінюється і їхній потенціал, причому між ними має місце лінійна залежність 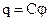. (7.34)

Коефіцієнт пропорційності 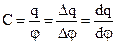, (7.35)

тобто відношення заряду провідника до його потенціалу називається електроємністю провідника. Одиницею вимірювання електроємності в системі СІ є фарада (Ф). Це електроємність такого провідника, при зміні заряду якого на 1Кл його потенціал змінюється на 1В. Менші одиниці електроємності: 1мкФ = 10^-6Ф, 1нФ = 10^-9Ф, 1пФ = 10^-12Ф.

Для системи провідників (конденсаторів) їхня взаємна електроємність 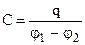, (7.36)

де різниця потенціалів між тілами, q – заряд одного із тіл.

Знайдемо електроємності простих конденсаторів.

Приклад 1. Електроємність сфери радіусом R.

Із (7.30) знаходимо 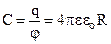. (7.37)

Приклад 2. Електроємність плоского конденсатора.

Як правило відстань між пластинами d набагато менша від розмірів пластин. Тому крайовими ефектами можна знехтувати і вважати поле між пластинами однорідним. Із (7.33) з врахуванням (7.24) одержуємо Тоді 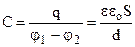. (7.38)

Приклад 3. Електроємність циліндричного конденсатора (рис.7.23). Це два коаксіальних циліндри. Із (7.27), враховуючи (7.22) і (7.6) знайдемо різницю потенціалів між циліндрами.

.

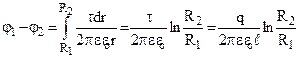Тоді 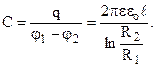(7.39)

Приклад 4. Електроємність сферичного конденсатора (рис.7.24).

Різницю потенціалів між сферами знайдемо врахувавши висновок розділу 7.3 і формулу (7.30).

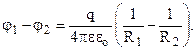Тоді електроємність 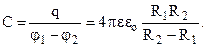(7.40)

Висновок. Приклади 1-4 і формули (7.37)-(7.40) показують , що електроємність не залежить від заряду, а визначається геометричними розмірами конденсаторів і властивостями діелектрика.

При з’єднанні конденсаторів у батареї загальна електроємність знаходиться так:

при паралельному з’єднанні як сума електроємностей конденсаторів;

(7.41)

при послідовному з’єднанні обернена електроємність батареї дорівнює сумі обернених електроємностей конденсаторів

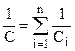. (7.42)

.

7.7 Енергія та густина енергії електростатичного поля

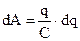Для того, щоб зарядити тіло необхідно виконати роботу по перенесенню порції заряду dq проти сил відштовхування від раніше перенесеного однойменного заряду q. Ця робота перетворюється в потенціальну енергію зарядженого тіла (в енергію електричного поля). Підставивши із (7.35), одержимо . Інтегрування в інтервалі від 0 до 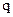із врахуванням (7.34) дає енергію

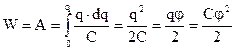. (7.43)

Густина енергії електростатичного поля – це енергія, яка зосереджена в одиниці об’єму простору, де це поле утворене

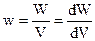
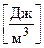(7.44)

Знайдемо її на прикладі плоского конденсатора (див. приклад 2 розділ 7.6). Об’єм . Із (7.38), (7.43), (7,44) і враховуючи (7.33), одержуємо

. (7.45)

8 Постійний електричний струм та його закони

8.1 Сила струму. Електрорушійна сила (е.р.с.). Напруга. Густина струму

Електричним струмом називається всякий направлений рух зарядів. За напрямок струму прийнятий напрямок руху позитивних зарядів. Для його існування необхідні дві умови:

– наявність рухомих зарядів;

– наявність сили, яка приводить ці заряди в направлений рух.

Наприклад, заряджене тіло переміщуємо у просторі мускульною силою руки. Це струм? Так. є заряд і є сила, яка його переміщує.

Найчастіше силою, яка переміщує заряд, виступає сила електричного поля. Робота цього поля витрачається на переміщення зарядів, і тому його енергія зменшується. Для того щоб струм протікав тривалий час, потрібно поповнювати енергію поля. Це відбувається в джерелах струму, або джерелах електрорушійної сили (е.р.с.). В них відбувається перетворення в електричну енергію різних видів енергії: механічної, оптичної, теплової, хімічної і т. ін., окрім електричної. Ці сили називаються сторонніми. Дійсно, в джерелах е.р.с. позитивні заряди рухаються проти електричного поля (від – до +) (рис.8.1). Такий їх рух не може здійснюватись силами електричного поля.

Робота по переміщенню заряду по дільниці кола, в якій є е.р.с., виконується силами електричного поля і сторонніми силами

.

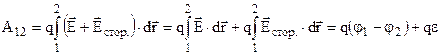Тут е.р.с. 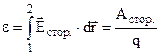- це робота, яку виконують сторонні сили по переміщенню одиничного позитивного заряду в середині джерела. Величина (8.1)

називається напругою. Це робота, яку виконують сили електричного поля і сторонні сили по переміщенню одиничного позитивного заряду із точки 1 в точку 2.

Силою струму I називається швидкість направленого переносу заряду

. (8.2)

Вимірюється струм у системі СІ в амперах (А). Це основна одиниця в цій системі і буде визначена по взаємодії провідників із струмом у розділі “електромагнетизм”.

Для характеристики розподілу струму по поперечному перетину провідника введена густина струму j – це струм, який протікає через одиницю поперечного перерізу

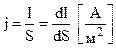. (8.3)

Не дивлячись, що струм величина скалярна, густина струму – це вектор, напрямок якого збігається з напрямком руху позитивних зарядів, тобто

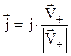. (8.4)

Струм, через густину струму знаходять шляхом інтегрування по площі перерізу провідника 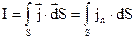. (8.5)

8.2 Основні положення класичної теорії електропровідності металів. Експериментальне підтвердження електронної природи струму в металах

Після відкриття у 1897 р. Дж. Томсоном електрона німецький фізик П. Друде у 1900 році заклав основи класичної теорії електропровідності металів, яка знайшла подальший розвиток у роботах нідерландського фізика Х. Лоренца. Розглянемо положення цієї електронної теорії Друде-Лоренца.

– Електронний газ в металах має властивості одноатомного молекулярного ідеального газу. Рухаючись хаотично, електрони зазнають зіткнень тільки з атомами кристалічної гратки, а не між собою, так як розміри електронів набагато менші, ніж атомів. Тому вважається, що середня довжина вільного пробігу електронів дорівнює міжатомній відстані і складає декілька ангстремів (1Å = 10^-10м).

– Так як теплові швидкості (середня арифметична, середня квадратична, найбільш ймовірна) із-за малої маси електронів дуже великі (~ 100 км/с), вважається що всі вони однакові. Тепловий хаотичний рух не приводить до направленого руху електронів, тобто струм не виникає.

– Під дією зовнішнього електричного поля виникає направлений рух електронів із швидкістю V, яка направлена проти напруженості поля. Знайдемо силу струму і його густину (рис.8.2). За час dt через перпендикулярний до вектора швидкості V переріз dS провідника перейдуть тільки ті носії, які знаходяться від нього на відстані не більшій, ніж 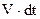і перенесуть свій заряд через цей переріз. Носії, які знаходяться далі, не встигнуть за цей час дійти до перерізу dS і внести вклад в електричний струм. Сумарний перенесений заряд дорівнює заряду носіїв, які знаходяться в зображеному циліндрі. 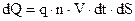(n - концентрація вільних носіїв заряду). Враховуючи (8.2) і (8.3), одержуємо струм 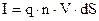та густину струму 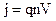. (8.6)

Оцінка значення швидкості V із формули (8.6) дає ~ 0,8 мм/с, що набагато менше, ніж теплова швидкість. Не дивлячись на це, струм у провіднику виникає практично миттєво, так як у направлений рух після вмикання електричного поля приходять усі електрони.

– Від зіткнення до зіткнення з атомами електрон рухається з середньою тепловою швидкістю. Вважається, що при зіткненні електрона з іоном кристалічної гратки він повністю втрачає набуту швидкість направленого руху. Отже направлений рух електрона між зіткненнями рівноприскорений без початкової швидкості направленого руху.

Розглянемо досліди, які підтверджують електронну природу струму в металах:

– Через послідовно з’єднані мідь-алюміній-мідь (рис.8.3) приблизно протягом року пропускався електричний струм, після чого досліджувались контакти на предмет взаємного проникнення металів. Не дивлячись на те, що в одному контакті струм протікав від міді до алюмінію, а в другому від алюмінію до міді, взаємне проникнення металів в обох контактах було однаковим. Стимульованої струмом дифузії виявлено не було. Це означає, що протікання струму в металах не супроводжується переносом речовини, а носіями струму являються загальні для всіх металів частинки – електрони.

– Металевий стержень, замкнутий чутливим гальванометром (рис.8.4), рухався, а потім різко зупинявся. Гальванометр фіксував імпульс струму, зумовлений тим, що в момент зупинки кристалічної гратки металу електрони ще продовжують рухатись по інерції в напрямку направленого руху.

– У 1913 році російські фізики Л.І.Мандельштам і М.Д.Папалексі вдосконалили вище розглянутий дослід. Вони замінили масивний провідник котушкою (довжина дроту ~500 м), яку привели в обертальні коливання (рис.8.5). В момент зміни напрямку руху котушки в ній виникав електричний струм, наявність якого фіксувалася телефоном, увімкнутим до кінців котушки (виникав характерний тріск). Тепер фіксувались уже не поодинокі імпульси струму.

–У 1916 році шотландський фізик Ч.Стюарт і американський Т.Толмен замінили в досліді Л.І.Мандельштама і М.Д.Папалексі телефон, чутливим гальванометром. Це дало можливість провести кількісні вимірювання, а саме визначити відношення заряду носіїв струму до їх маси (питомій заряд). Виявилось, що це відношення дорівнює питомому заряду електрона.

Отже струм у металах зумовлений направленим рухом електронів.

8.3 Закон Ома по класичній теорії електропровідності металів. Електричний опір провідників

Запишемо другий закон Ньютона для направленого руху електрона 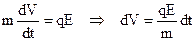. Інтегруємо це рівняння в межах швидкості від 0 до V_макс, і в межах часу від 0 до τ. – час вільного пробігу електрона 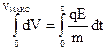. Одержуємо

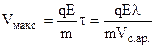. (8.7)

Середня швидкість направленого руху V дорівнює півсумі початкової (V₀ = 0, див положення 4) і кінцевої V_макс. Враховуючи (8.6), густина струму , або . (8.8)

Це і є закон Ома в диференційній формі. Тут питома електропровідність 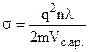. (8.9)

Величина обернена питомій електропровідності називається питомим опором ρ

. (8.10)

Це опір суцільного куба з ребром 1м при протіканні струму між протилежними гранями.

Одержимо закон Ома в інтегральній формі. Для цього рівняння (8.8) домножаємо скалярно на вектор переміщення вздовж провідника в напрямку протікання струму і інтегруємо в межах двох точок провідника 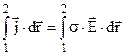. Врахуємо (7.27), 8.1) і що кут між векторами 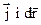дорівнює нулю, одержуємо .

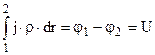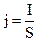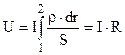. . (8.11)

Тут U – напруга, R – опір провідника

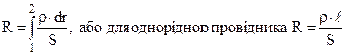(8.12)

залежить від матеріалу і геометричних розмірів: площі перерізу S та довжини ℓ.

Приклад. Знайти опір R однорідного провідника у формі зрізаного конуса при протіканні струму між його основами (рис.8.6). Задані геометричні розміри R₁, R₂ і питомий опір ρ.

Елемент dx довжини провідника має переріз радіусом 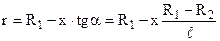. Тоді опір цього елементу .

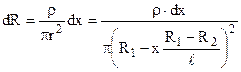Загальний опір .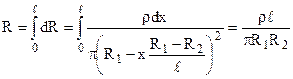

При з’єднанні резисторів загальний опір знаходиться так:

при послідовному з’єднанні як сума опорів;

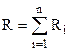, (8.13)

при паралельному – обернений опір дорівнює сумі обернених опорів 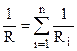. (8.14)

8.4 Закон Джоуля-Ленца по класичній теорії електропровідності металів

Закон Джоуля –Ленца – це закон про теплову дію електричного струму: якщо електричний струм не виконує механічної роботи, то вся його енергія перетворюється в тепло. Який механізм нагрівання провідників електричним струмом? Електрон прискорюється електричним полем. Швидкість і кінетична енергія його поступального руху зростають за рахунок енергії електричного поля. При зіткненні з вузлом кристалічної гратки він повністю втрачає набуту швидкість, а значить і кінетичну енергію направленого руху (див. положення 4, розділ 8.2). Ця енергія передається атому кристалічної гратки, внаслідок чого він починає коливатись більш інтенсивно. А це і означає нагрівання кристалу.

Знайдемо питому потужність w, тобто енергію, яка виділяється в одиниці об’єму провідника за одиницю часу

. (8.15)

За час dt кожний електрон зазнає 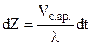зіткнень, при кожному з яких кристалу буде передана енергія 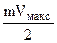. В об’ємі dV_об знаходиться 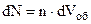електронів. Тоді

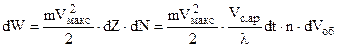. Підставляємо в (8.15). З врахуванням (8.7 ) і (8.9 ), після спрощень, одержуємо

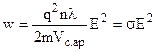. Якщо скористатися законом Ома (8.8 ), закон Джоуля-Ленца в диференційній формі запишеться так:

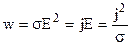. (8.16)

В інтегральній формі цей закон має вид

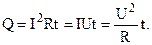(8.17)

Для потужності електричного струму маємо

(8.18)

8.5 Закон Відемана-Франца по класичній теорії електропровідності металів

Дослідами встановлено, що метали наряду з високою електропровідністю мають і хорошу теплопровідність, які значно перевищують електропровідність і теплопровідність діелектриків. Логічно припустити, що ця різниця властивостей зумовлена наявністю електронного газу в металах і його відсутністю в діелектриках.