Рідини. Явища в рідинах 1 страница

 По характеру руху молекул і сил взаємодії між ними рідини займають проміжне положення між газами і твердими тілами. В рідинах молекули протягом певного часу здійснюють коливання навколо тимчасового положення рівноваги. Цей час називається часом осідлого стану молекули. Потім молекула перескакує в інше положення рівноваги (рис.6.37). Ці хаотичні переходи нагадують рух молекул газу, а коливальний рух – рух атомів у твердих тілах. Для рідин характерний ближній порядок в розміщенні молекул. Це означає, що розміщення найближчих сусідніх молекул однакове для всіх молекул. Але по мірі віддалення такий порядок порушується. Твердим же кристалічним тілам характерний дальній порядок в розміщенні молекул. У зв’язку з цим для кристалів має місце анізотропія властивостей (різні властивості в різних напрямках), а для рідин характерні ізотропні (однакові в різних напрямках) властивості. Але існують так звані рідкі кристали, названі так із-за анізотропії своїх властивостей, яка зумовлена анізотропією властивостей окремих молекул, а не дальнім порядком в їх розміщенні. Молекули рідких кристалів уявляють собою довгі ланцюги полімерних сполук. При паралельній одна одній орієнтації молекул і виникає анізотропія.
По характеру руху молекул і сил взаємодії між ними рідини займають проміжне положення між газами і твердими тілами. В рідинах молекули протягом певного часу здійснюють коливання навколо тимчасового положення рівноваги. Цей час називається часом осідлого стану молекули. Потім молекула перескакує в інше положення рівноваги (рис.6.37). Ці хаотичні переходи нагадують рух молекул газу, а коливальний рух – рух атомів у твердих тілах. Для рідин характерний ближній порядок в розміщенні молекул. Це означає, що розміщення найближчих сусідніх молекул однакове для всіх молекул. Але по мірі віддалення такий порядок порушується. Твердим же кристалічним тілам характерний дальній порядок в розміщенні молекул. У зв’язку з цим для кристалів має місце анізотропія властивостей (різні властивості в різних напрямках), а для рідин характерні ізотропні (однакові в різних напрямках) властивості. Але існують так звані рідкі кристали, названі так із-за анізотропії своїх властивостей, яка зумовлена анізотропією властивостей окремих молекул, а не дальнім порядком в їх розміщенні. Молекули рідких кристалів уявляють собою довгі ланцюги полімерних сполук. При паралельній одна одній орієнтації молекул і виникає анізотропія.
В рідинах спостерігаються ряд специфічних для них властивостей:
1) поверхнева енергія; 2) сила поверхневого натягу; 3) поверхневий тиск; 4) змочування і незмочування 5) капілярні.
Розглянемо кожне із них.

 – Поверхнева енергія. Розглянемо сили, які діють з боку сусідніх молекул на дві молекули рідини (рис.6.38): об’ємну (А) і поверхневу (В). Оточення об’ємної молекули А симетричне, тому рівнодіюча сил дорівнює нулю. На поверхневу молекулу В діють сили з боку рідини більші, ніж з боку газу. Виникає рівнодіюча сила, направлена всередину рідини. Отже для переведення молекули з об’єму на поверхню необхідно виконати роботу проти цієї рівнодіючої. Ця робота перетворюється в потенціальну енергію поверхневих молекул.
– Поверхнева енергія. Розглянемо сили, які діють з боку сусідніх молекул на дві молекули рідини (рис.6.38): об’ємну (А) і поверхневу (В). Оточення об’ємної молекули А симетричне, тому рівнодіюча сил дорівнює нулю. На поверхневу молекулу В діють сили з боку рідини більші, ніж з боку газу. Виникає рівнодіюча сила, направлена всередину рідини. Отже для переведення молекули з об’єму на поверхню необхідно виконати роботу проти цієї рівнодіючої. Ця робота перетворюється в потенціальну енергію поверхневих молекул.
Поверхнева енергія US дорівнює різниці енергії поверхневих молекул і енергії такої ж кількості об’ємних молекул. Ясно, що вона пропорційна кількості поверхневих молекул, тобто площі поверхні рідини S 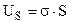 . (6.78)
. (6.78)
Тут 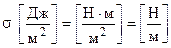 - коефіцієнт поверхневого натягу, для кожної рідини величина стала, але залежить від температури і домішок.
- коефіцієнт поверхневого натягу, для кожної рідини величина стала, але залежить від температури і домішок.
 – Сила поверхневого натягу. Відомо (розділ 4.7), що стійкою рівновагою системі є стан з мінімальною потенціальною енергією. Тому рідина має тенденцію зайняти стан з мінімальною площею поверхні, тобто скоротитись. Це приводить до виникнення сили поверхневого натягу, яка діє вздовж
– Сила поверхневого натягу. Відомо (розділ 4.7), що стійкою рівновагою системі є стан з мінімальною потенціальною енергією. Тому рідина має тенденцію зайняти стан з мінімальною площею поверхні, тобто скоротитись. Це приводить до виникнення сили поверхневого натягу, яка діє вздовж  межі поверхні по дотичній до неї. Знайдемо величину цієї сили F. Нехай на прямокутну рамку з рухомою
межі поверхні по дотичній до неї. Знайдемо величину цієї сили F. Нехай на прямокутну рамку з рухомою  стороною
стороною 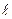 натягнута плівка рідини (рис.6.39). Розтягнемо плівку силою F на відстань х. Таке розтягування фактично є не що інше, як процес переводу молекул із об’єму рідини на поверхню. Буде виконана робота А = F∙x, яка дорівнює
натягнута плівка рідини (рис.6.39). Розтягнемо плівку силою F на відстань х. Таке розтягування фактично є не що інше, як процес переводу молекул із об’єму рідини на поверхню. Буде виконана робота А = F∙x, яка дорівнює  збільшенню поверхневої енергії
збільшенню поверхневої енергії 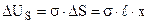 . Одержуємо для сили поверхневого натягу
. Одержуємо для сили поверхневого натягу 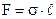 . (6.79)
. (6.79)
Силою поверхневого натягу рідина уже стиснута. Цим і пояснюється погана стискуваність рідин.

 – Поверхневий тиск. Коли поверхня рідини викривлена (утворився меніск), її площа більша, ніж плоскої поверхні і поверхнева енергія не мінімальна. Тенденція поверхні до скорочення приводить до виникнення сили, яка направлена до центру кривизни поверхні. Виникає поверхневий тиск РS (рис.6.40). Знайдемо його величину на прикладі краплини рідини, яка має форму кулі радіусом R (таку форму буде мати рідина у стані невагомості). Уявно розріжемо її діаметральною площиною (рис.6.41). Вздовж лінії перерізу (кола) діє сила поверхневого натягу
– Поверхневий тиск. Коли поверхня рідини викривлена (утворився меніск), її площа більша, ніж плоскої поверхні і поверхнева енергія не мінімальна. Тенденція поверхні до скорочення приводить до виникнення сили, яка направлена до центру кривизни поверхні. Виникає поверхневий тиск РS (рис.6.40). Знайдемо його величину на прикладі краплини рідини, яка має форму кулі радіусом R (таку форму буде мати рідина у стані невагомості). Уявно розріжемо її діаметральною площиною (рис.6.41). Вздовж лінії перерізу (кола) діє сила поверхневого натягу 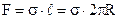 , яка і стискує дві півкулі. Ця сила розподіляється по площі перерізу
, яка і стискує дві півкулі. Ця сила розподіляється по площі перерізу 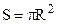 . Виникає поверхневий тиск, направлений до центра кулі
. Виникає поверхневий тиск, направлений до центра кулі
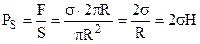 . (6.80)
. (6.80)

 Тут
Тут 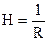 - кривизна сферичної поверхні. Якщо ж поверхня не сферична, то її кривизна визначається як півсума обернених радіусів кривизни R1 і R2 ліній перетину цієї поверхні двома будь-якими взаємно-перпендикулярними площинами (рис.6.42)
- кривизна сферичної поверхні. Якщо ж поверхня не сферична, то її кривизна визначається як півсума обернених радіусів кривизни R1 і R2 ліній перетину цієї поверхні двома будь-якими взаємно-перпендикулярними площинами (рис.6.42)
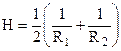 . (6.81)
. (6.81)

 Наприклад, для циліндричного меніска (рис.6.43) кривизна
Наприклад, для циліндричного меніска (рис.6.43) кривизна 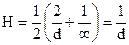 .
.

 – Явище змочування і не змочування. На поверхневу молекулу, яка межує з поверхнею твердого тіла і газом діють сили: Fт.р – на межі тверда поверхня-рідина; Fт..г – на межі тверде тіло-газ; Fр..г – на межі рідина-газ (рис.6.44). Умовою рівноваги цієї молекули є рівняння
– Явище змочування і не змочування. На поверхневу молекулу, яка межує з поверхнею твердого тіла і газом діють сили: Fт.р – на межі тверда поверхня-рідина; Fт..г – на межі тверде тіло-газ; Fр..г – на межі рідина-газ (рис.6.44). Умовою рівноваги цієї молекули є рівняння
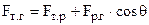 , (6.82)
, (6.82)

 де θ – крайовий кут – це кут між дотичною до поверхні та межею між рідиною і твердою поверхнею, відрахований в середині рідини. Із (6.82)
де θ – крайовий кут – це кут між дотичною до поверхні та межею між рідиною і твердою поверхнею, відрахований в середині рідини. Із (6.82) 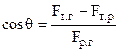 . В залежності від співвідношення сил, крайовий кут може мати значення від 0о до 180о. Якщо кут 0о ≤ θ < 90о гострий, рідина змочує поверхню (рис.6.45,а). Якщо ж кут 90о ≤ θ ≤180о тупий, рідина не змочує поверхню (рис.6.45,б). Саме явище змочування чи незмочування твердої поверхні і є причиною викривлення поверхні рідини, тобто утворення меніску.
. В залежності від співвідношення сил, крайовий кут може мати значення від 0о до 180о. Якщо кут 0о ≤ θ < 90о гострий, рідина змочує поверхню (рис.6.45,а). Якщо ж кут 90о ≤ θ ≤180о тупий, рідина не змочує поверхню (рис.6.45,б). Саме явище змочування чи незмочування твердої поверхні і є причиною викривлення поверхні рідини, тобто утворення меніску.
 – Капілярні явища – заключаються у зміні рівня рідини у вузьких каналах (капілярах) порівняно з її рівнем у широкій посудині (рис.6.46).
– Капілярні явища – заключаються у зміні рівня рідини у вузьких каналах (капілярах) порівняно з її рівнем у широкій посудині (рис.6.46).  Рідина піднімається, або опускається за рахунок поверхневого тиску меніску рідини, який утворюється при змочуванні чи не змочуванні рідиною поверхні капіляру. Зміна висоти рівня припиняється тоді, коли поверхневий тиск зрівноважується гідростатичним тиском стовпчика рідини
Рідина піднімається, або опускається за рахунок поверхневого тиску меніску рідини, який утворюється при змочуванні чи не змочуванні рідиною поверхні капіляру. Зміна висоти рівня припиняється тоді, коли поверхневий тиск зрівноважується гідростатичним тиском стовпчика рідини 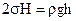 . (ρ – густина рідини). Отже, різниця рівнів рідини в капілярі
. (ρ – густина рідини). Отже, різниця рівнів рідини в капілярі 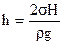 . (6.83)
. (6.83)
Кривизну меніска знайдемо через геометричні розміри капіляра і крайовий кут.
У циліндричному капілярі меніск має сферичну поверхню, кривизна якої 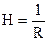 . Із рис.6.46 знаходимо
. Із рис.6.46 знаходимо 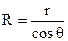 . Таким чином, для циліндричного капіляра
. Таким чином, для циліндричного капіляра
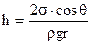 . (6.84)
. (6.84)
Якщо капіляр утворений двома паралельними площинами, відстань між якими r, меніск має циліндричну поверхню. Тому кривизна 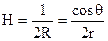 , а висота
, а висота 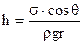 . (6.85)
. (6.85)
 6.28 Фазові переходи. Діаграма стану речовини. Рівняння Клапейрона-Клаузіуса
6.28 Фазові переходи. Діаграма стану речовини. Рівняння Клапейрона-Клаузіуса
 Фазою називається однакові за фізичними властивостями частини системи. На рис.6.47 зображені три фази: вода, лід, пара.
Фазою називається однакові за фізичними властивостями частини системи. На рис.6.47 зображені три фази: вода, лід, пара.
Перехід речовини із однієї фази в іншу називається фазовим переходом. Розрізняють фазові переходи 1-го і 2-го роду. При фазових переходах 1-го роду виділяється, або поглинається прихована теплота переходу. Наприклад, плавлення (кристалізація)
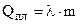 , (6.86)
, (6.86)
випаровування (конденсація)
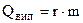 . (6.87)
. (6.87)
Тут λ і r – питомі теплоти плавлення і випаровування відповідно.
 При фазових переходах 2-го роду прихована теплота не проявляється, але відбувається стрибкоподібна зміна певних фізичних властивостей. Як правило такі переходи супроводжується стрибкопо
При фазових переходах 2-го роду прихована теплота не проявляється, але відбувається стрибкоподібна зміна певних фізичних властивостей. Як правило такі переходи супроводжується стрибкопо  дібною зміною теплоємності. Тому теплоємність може слугувати як індикатор фазових переходів 2-го роду. Прикладами таких переходів є перехід графіту в алмаз (змінюється твердість), перехід у надпровідний стан (змінюється електропровідність), перехід феромагнетику в парамагнетик при нагріванні (змінюється магнітна проникність), перехід у надтекучий стан (змінюється коефіцієнт в’язкості) і т.д.
дібною зміною теплоємності. Тому теплоємність може слугувати як індикатор фазових переходів 2-го роду. Прикладами таких переходів є перехід графіту в алмаз (змінюється твердість), перехід у надпровідний стан (змінюється електропровідність), перехід феромагнетику в парамагнетик при нагріванні (змінюється магнітна проникність), перехід у надтекучий стан (змінюється коефіцієнт в’язкості) і т.д.

 При певних умовах різні фази речовини можуть знаходитись у рівновазі при контакті однієї фази з іншою. Такий стан має місце при певних зовнішніх умовах (температура Т, тиск Р, ... ). Сукупність станів рівноваги різних фаз в координатах Р-Т називається діаграмою стану речовини (рис.6.48). Лінія АТ - крива сублімації, ВТ - крива випаровування, СТ – крива плавлення. Точка діаграми стану відповідає рівновазі відповідних фаз, тобто відповідають умовам відповідного фазового переходу. Звертає на себе увагу точка Т рівноваги трьох фаз. Ця точка називається потрійною точкою. Для різних речовин параметри потрійної точки різні. Наприклад, для води: Р3 = 4,58 мм рт.ст.,
При певних умовах різні фази речовини можуть знаходитись у рівновазі при контакті однієї фази з іншою. Такий стан має місце при певних зовнішніх умовах (температура Т, тиск Р, ... ). Сукупність станів рівноваги різних фаз в координатах Р-Т називається діаграмою стану речовини (рис.6.48). Лінія АТ - крива сублімації, ВТ - крива випаровування, СТ – крива плавлення. Точка діаграми стану відповідає рівновазі відповідних фаз, тобто відповідають умовам відповідного фазового переходу. Звертає на себе увагу точка Т рівноваги трьох фаз. Ця точка називається потрійною точкою. Для різних речовин параметри потрійної точки різні. Наприклад, для води: Р3 = 4,58 мм рт.ст., 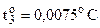 .Кожна точка діаграми стану відповідає умовам відповідного фазового переходу. Отже, при зміні тиску dP змінюється і температура фазового переходу на dT (рис.6.49). Таку зміну описує рівняння Клапейрона-Клаузіуса
.Кожна точка діаграми стану відповідає умовам відповідного фазового переходу. Отже, при зміні тиску dP змінюється і температура фазового переходу на dT (рис.6.49). Таку зміну описує рівняння Клапейрона-Клаузіуса
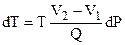 . (6.88)
. (6.88)
Тут: V2 і V1 – об’єми речовини відповідно після і до фазового переходу, Q – прихована теплота фазового переходу.
Наприклад, відомо, що при плавленні льоду об’єм речовини зменшується V2 < V1. Для плавлення потрібно затратити тепло, тобто Q < 0. Отже, при dP > 0 збільшенні тиску dT < 0 температура плавлення зменшується, і може стати меншою 0оС. Таке явище має місце під ковзанами спортсменів. Утворювана під ковзанами вода виконує роль змащування і зменшує тертя. Аналогічно пояснюється і зменшення температури кипіння води в горах при зниженому тискові.
7 Електродинаміка. Електростатика
7.1 Поняття про заряд. Закон збереження заряду. Взаємодія зарядів. Закон Кулона. Силові характеристики поля
Дослідами по взаємодії тіл встановлено, що деякі тіла взаємодіють з силами, набагато більшими (приблизно в 1039 разів), ніж сила гравітаційної взаємодії. Таким тілам приписали властивість мати заряд. Всі заряди умовно поділені на позитивні і негативні у відповідності з двозначним характером їх взаємодії: однойменні заряди відштовхуються, різнойменні притягуються. Сучасній науці відомо, що носіями заряду являються електрони та іони. Елементарним (найменшим) зарядом є заряд електрона е = -1,6∙10-19 Кл. Кл (кулон) це одиниця заряду в системі одиниць СІ. У всіх електричних явищах має місце закон збереження заряду - алгебраїчна сума зарядів замкнутої (ізольованої) системи не змінюється.
 В основі електростатики, тобто вчення про взаємодію нерухомих зарядів, лежить закон Кулона (1785р.) для точкових зарядів:
В основі електростатики, тобто вчення про взаємодію нерухомих зарядів, лежить закон Кулона (1785р.) для точкових зарядів:
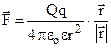
 (7.1)
(7.1)
Сила 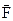 , з якою взаємодіють два точкових заряди Q і q прямо пропорційна добуткові цих зарядів, обернено пропорційна квадрату відстані r між ними і направлена по лінії, що з’єднує ці заряди
, з якою взаємодіють два точкових заряди Q і q прямо пропорційна добуткові цих зарядів, обернено пропорційна квадрату відстані r між ними і направлена по лінії, що з’єднує ці заряди
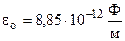 - діелектрична стала, яка не має фізичного змісту, а введена для узгодження одиниць вимірювання в системі СІ;
- діелектрична стала, яка не має фізичного змісту, а введена для узгодження одиниць вимірювання в системі СІ; 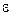 - відносна діелектрична проникність середовища, яка показує у скільки разів сила взаємодії у вакуумі Fo більша, ніж сила взаємодії F в даному середовищі. Для повітря і вакууму
- відносна діелектрична проникність середовища, яка показує у скільки разів сила взаємодії у вакуумі Fo більша, ніж сила взаємодії F в даному середовищі. Для повітря і вакууму 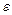 = 1.
= 1.
По сучасним поглядам, взаємодія зарядів відбувається через особливу форму матерії – електричне поле. Кожний заряд утворює у навколишньому середовищі електричне поле, яке і діє на внесений у нього заряд.
Силовою характеристикою електростатичного поля є напруженість
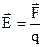
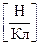 (7.2)
(7.2)
Ця векторна величина дорівнює силі, яка діє з боку поля на одиничний позитивний пробний заряд. Для поля точкового заряду Q напруженість
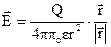 (7.3)
(7.3)
 |
Вектор
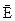 направлений по радіальним лініям від заряду Q, якщо він позитивний, і до нього, якщо він негативний.
направлений по радіальним лініям від заряду Q, якщо він позитивний, і до нього, якщо він негативний.
Вектор 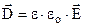 називається вектором індукції електростатичного поля. Це теж силова, векторна характеристика поля, але на відміну від напруженості, вона не залежить від властивостей середовища. Дійсно, для точкового заряду, враховуючи (7.3), маємо
називається вектором індукції електростатичного поля. Це теж силова, векторна характеристика поля, але на відміну від напруженості, вона не залежить від властивостей середовища. Дійсно, для точкового заряду, враховуючи (7.3), маємо
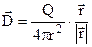 . (7.4)
. (7.4)
Діелектричні властивості середовища (ε і εо) в цій формулі відсутні.

 |
Графічно електростатичне поле зображається силовими лініями. Це лінії, дотична до яких в кожній точці співпадає з вектором напруженості
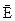 (індукції
(індукції 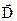 ) (рис.7.1). Силові лінії починаються на позитивних і закінчуються на негативних зарядах. Вони не перетинаються, так як вектори напруженості і індукції однозначні. У точці ж перетину напрямок цих векторів не визначений.
) (рис.7.1). Силові лінії починаються на позитивних і закінчуються на негативних зарядах. Вони не перетинаються, так як вектори напруженості і індукції однозначні. У точці ж перетину напрямок цих векторів не визначений.
По густині силових ліній можна судити про величину 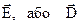 . Вони більші там, де густина ліній більша.
. Вони більші там, де густина ліній більша.
7.2 Принцип суперпозиції та його застосування до розрахунку
електростатичного поля

 Якщо поле утворене декількома зарядами, то вектор напруженості результуючого поля знаходиться по принципу суперпозиції, як векторна сума напруженостей, утворених в даній точці кожним зарядом незалежно від інших зарядів (рис.7.2).
Якщо поле утворене декількома зарядами, то вектор напруженості результуючого поля знаходиться по принципу суперпозиції, як векторна сума напруженостей, утворених в даній точці кожним зарядом незалежно від інших зарядів (рис.7.2).
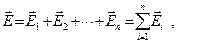
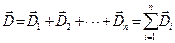 . (7.5)
. (7.5)
Ступінь зарядженості тіл, які не можна вважати точковими, характеризуються такими величинами:
лінійна густина заряду – заряд одиниці довжини
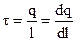

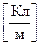 ; (7.6)
; (7.6)
поверхнева густина заряду – заряд одиниці площі
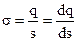

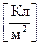 ; (7.7)
; (7.7)
об’ємна густина заряду – заряд одиниці об’єму
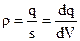

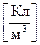 . (7.8)
. (7.8)
Для полів, утворених неточковими зарядами, напруженість розраховується також по принципу суперпозиції, але формула (7.5) переходить у відповідний ( криволінійний, поверхневий чи об’ємний ) інтеграли
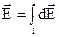 ,
, 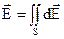 ,
, 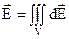 , (7.9)
, (7.9)
де 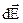 - напруженість поля, створеного нескінченно малим елементом тіла dl, dS чи dV. Розглянемо декілька прикладів застосування принципу суперпозиції для розрахунку поля заряджених тіл.
- напруженість поля, створеного нескінченно малим елементом тіла dl, dS чи dV. Розглянемо декілька прикладів застосування принципу суперпозиції для розрахунку поля заряджених тіл.
 Приклад 1. Розрахувати напруженість електричного поля на осі зарядженого кільця радіусом R, зарядом Q на відстані h від центра кільця (рис.7.3).
Приклад 1. Розрахувати напруженість електричного поля на осі зарядженого кільця радіусом R, зарядом Q на відстані h від центра кільця (рис.7.3).
Елемент dl1 кільця, заряд якого 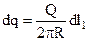 , створює напруженість поля
, створює напруженість поля 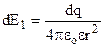 . (7.10)
. (7.10)
 Діаметрально протилежний елемент dl2 створює напруженість dE2. Ясно, що Х–ві проекції цих векторів попарно компенсуються, а У-ві – додаються.
Діаметрально протилежний елемент dl2 створює напруженість dE2. Ясно, що Х–ві проекції цих векторів попарно компенсуються, а У-ві – додаються.
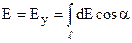 . Враховуючи (7.10), і що
. Враховуючи (7.10), і що 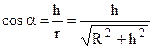 , одержуємо
, одержуємо 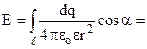

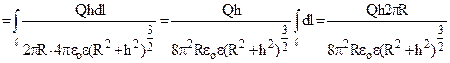
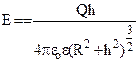 . (7.11)
. (7.11)
При h =0 ( в центрі кільця) Е=0. При h → ∞ Е = 0.
Приклад 2. Розрахувати поле нескінченної зарядженої осі в точці, яка знаходиться на відстані R від неї. Лінійна густина заряду осі дорівнює τ (рис.7.4).
 Нескінченно малий елемент dℓ(точковий заряд) створює напруженіcть
Нескінченно малий елемент dℓ(точковий заряд) створює напруженіcть 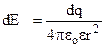 . Заряд цього елемента дорівнює
. Заряд цього елемента дорівнює 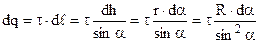 . Відстань
. Відстань 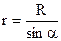 . Одержуємо
. Одержуємо 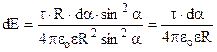 . Знаходимо проекції цього вектора на осі координат:
. Знаходимо проекції цього вектора на осі координат: 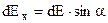 ,
, 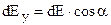 . Інтегрування по всій осі зводиться до інтегрування по куту α в межах від 0 до π.
. Інтегрування по всій осі зводиться до інтегрування по куту α в межах від 0 до π.
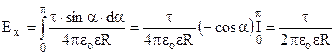 . (7.12)
. (7.12)
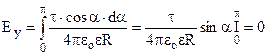 .
.
Так як Еу = 0, вектор напруженості направлений вздовж осі ох, тобто перпендикулярно до зарядженої осі.
Приклад 3. Розрахувати поле нескінченної зарядженої площини з поверхневою густиною заряду σ (рис.7.5).
Положення нескінченно малого елемента dS, заряд якого dq = σ∙dS,
задамо полярними координатами ρ і α. В цих координатах dS = ρ∙dρ∙dα. Знайдемо dEz , яка перпендикулярна до площини. 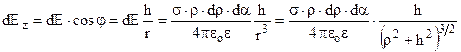 Щоб охопити всю площину, кут α повинен змінюватись від 0 до 2π, а радіус ρ – від 0 до ∞. Беремо подвійний інтеграл в цих межах
Щоб охопити всю площину, кут α повинен змінюватись від 0 до 2π, а радіус ρ – від 0 до ∞. Беремо подвійний інтеграл в цих межах

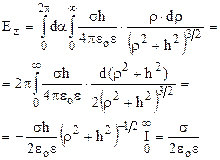

 Проекція вектора напруженості на площину, перпендикулярну до осі ОZ дорівнює нулю. В цьому можна впевнитись математично, замінивши соsφ на sinφ, а можна і такими міркуваннями: на нескінченній площині завжди можна знайти елемент dS2,
Проекція вектора напруженості на площину, перпендикулярну до осі ОZ дорівнює нулю. В цьому можна впевнитись математично, замінивши соsφ на sinφ, а можна і такими міркуваннями: на нескінченній площині завжди можна знайти елемент dS2,  симетричний dS1 відносно перпендикуляра h до площини (рис7.6). Ці елементи створюють однакові вектори напруженості dE1 і dE2, Z-ві проекції яких співпадають, а перпендикулярні проекції взаємно протилежні і тому компенсують одна одну. Отже вектор напруженості поля нескінченної зарядженої площини
симетричний dS1 відносно перпендикуляра h до площини (рис7.6). Ці елементи створюють однакові вектори напруженості dE1 і dE2, Z-ві проекції яких співпадають, а перпендикулярні проекції взаємно протилежні і тому компенсують одна одну. Отже вектор напруженості поля нескінченної зарядженої площини
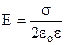 (7.13)
(7.13)
перпендикулярний до неї і не залежить від положення точки, тобто однакове в усіх точках простору. Такі поля називаються однорідними.
7.3 Теорема Остроградського-Гаусса та її застосування до розрахунку електростатичного поля заряджених тіл
Для спрощення розрахунку полів симетричних заряджених тіл застосовується теорема Остроградського – Гауса: потік вектора електростатичної індукції через будь-яку замкнуту поверхню дорівнює алгебраїчній сумі зарядів, охоплених цією поверхнею. 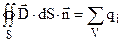 . (7.14)
. (7.14)

 Потоком dФ вектора
Потоком dФ вектора 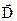 через площадку dS називається добуток вектора
через площадку dS називається добуток вектора 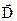 на величину площадки dS і на косинус кута α між вектором
на величину площадки dS і на косинус кута α між вектором 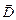 і нормальним до площадки dS одиничним вектором
і нормальним до площадки dS одиничним вектором 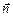 (рис.7.7).
(рис.7.7).
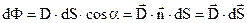 . (7.15)
. (7.15)

 Площадку dS вважають вектором, який за напрямком співпадає з вектором
Площадку dS вважають вектором, який за напрямком співпадає з вектором 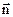 . Якщо заряд, наприклад, q1 знаходиться за межами замкнутої
. Якщо заряд, наприклад, q1 знаходиться за межами замкнутої  поверхні (рис.7.8), потік дорівнює нулю. Дійсно, скільки силових ліній входить в об’єм, обмежений поверхнею, стільки ж і виходить. Силові ж лінії від заряду q2, який знаходиться всередині поверхні, тільки виходять з неї.
поверхні (рис.7.8), потік дорівнює нулю. Дійсно, скільки силових ліній входить в об’єм, обмежений поверхнею, стільки ж і виходить. Силові ж лінії від заряду q2, який знаходиться всередині поверхні, тільки виходять з неї.
Розглянемо приклади застосування цієї теореми.
Приклад 1. Напруженість поля точкового заряду.
Поверхню S вибираємо у вигляді сфери радіусом r, в центрі якої знаходиться заряд q (рис.7.9).
 По теоремі Остроградського-Гауса маємо
По теоремі Остроградського-Гауса маємо
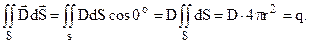
Для різних точок сфери вектор D однаковий за величиною, так як всі вони однаково розміщені по відношенню до заряду q. Тому його винесли за знак інтегралу. А 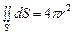 дає площу поверхні сфери. Одержуємо
дає площу поверхні сфери. Одержуємо

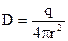 і
і 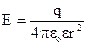 . (7.16)
. (7.16)
Приклад 2. Поле зарядженої по поверхні до заряду q металевої кулі радіусом R (рис.7.10).
 Для r < R
Для r < R 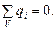 Тому D = 0 і Е = 0. Поле всередині провідників відсутнє. При r > R аналогічно прикладу 2,
Тому D = 0 і Е = 0. Поле всередині провідників відсутнє. При r > R аналогічно прикладу 2,
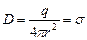 і
і 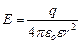 . (7.17)
. (7.17)
 Графік залежності індукції D від радіуса r показана на рис.7.12. На поверхні кулі індукція зазнає стрибкоподібної зміни на величину σ поверхневої густини вільних зарядів.
Графік залежності індукції D від радіуса r показана на рис.7.12. На поверхні кулі індукція зазнає стрибкоподібної зміни на величину σ поверхневої густини вільних зарядів.

 Приклад 3. Поле рівномірно зарядженої по об’єму до заряду q кулі радіусом R (рис.7.13).
Приклад 3. Поле рівномірно зарядженої по об’єму до заряду q кулі радіусом R (рис.7.13).
Для r>R аналогічно прикладу 2 і 3
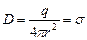 і
і 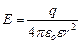 . (7.18)
. (7.18)
 Об’ємна густина заряду
Об’ємна густина заряду 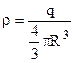 . Вирази (7.18) приймуть вид
. Вирази (7.18) приймуть вид
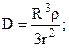
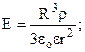 (7.19)
(7.19)
При r<R одержуємо 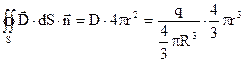 .
.
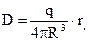
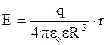 , (7.20)
, (7.20)
або через густину заряду 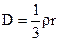 і
і 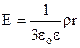 (7.21)
(7.21)
 Графік залежності індукції D від радіуса r показана на рис.7.14. При r = R вирази (7.18) і (7.20) дають однакову величину D. Отже на поверхні кулі вектор індукції розриву не зазнає.
Графік залежності індукції D від радіуса r показана на рис.7.14. При r = R вирази (7.18) і (7.20) дають однакову величину D. Отже на поверхні кулі вектор індукції розриву не зазнає.
Дата добавления: 2015-06-17; просмотров: 1308;
