Рідини. Явища в рідинах 4 страница

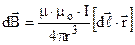, (9.4)

або в скалярній формі

. (9.5)

Тут: μ – відносна магнітна проникність середовища, показує у скільки разів індукція поля в середовищі більша, ніж у вакуумі. Це безрозмірна величина; μ_о = 4∙π∙10^-7 Гн/м – магнітна стала, введена в системі СІ для узгодження одиниць вимірювання. В електростатиці аналогічною є електрична стала ε_о.

Окрім індукції, аналогічно електростатичному полю, вводиться ще одна силова характеристика магнітного поля – напруженість

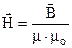. (9.6)

Закон Біо-Савара-Лапласа для напруженості

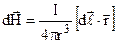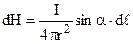, або (9.7)

показує, що вона не залежить від магнітних властивостей середовища. Вимірюється напруженість в А/м.

Закон Біо-Савара-Лапласа в магнетизмі аналогічний закону Кулона в електростатиці. Він використовується для розрахунку магнітних полів, утворених провідниками із струмом різних за формою, виходячи із принципу суперпозиції: індукція (напруженість) магнітного поля будь-якого провідника із струмом дорівнює векторній сумі індукцій (напруженостей), створених у даній точці кожним елементом 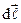провідника. Для цього необхідно розрахувати криволінійні інтеграли

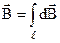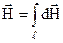, . (9.8)

Принцип суперпозиції використовується і для розрахунку магнітного поля декількох джерел, наприклад, провідників із струмом. Результуюче поле є векторною сумою полів від кожного джерела.

9.3 Застосування закону Біо-Савара-Лапласа і принципу суперпозиції для розрахунку магнітного поля на осі колового струму

Знайдемо напруженість магнітного поля на осі колового провідника радіусом R, по якому тече струм І. Положення точки задамо висотою h від центра кола (рис.9.6). Спочатку визначимо напрямок вектора 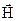. Для цього виберемо два однакових діаметрально протилежних елементи провідника . Вони створюють у даній точці вектори напруженості 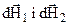, які перпендикулярні до відповідних радіус-векторів і однакові за величиною. Спроектуємо ці вектори напруженостей на осі x і y. З рисунка видно, що , тобто попарно компенсуються. Проекції на вісь у направлені паралельно, тому будемо додавати їх алгебраїчно. Таким чином результую чий вектор направлений вздовж осі кільця у відповідності з правилом правого гвинта: якщо обертати гвинт в напрямку струму, його поступальний рух вздовж осі вказує напрямок вектора напруженості.

По принципу суперпозиції (9.8), враховуючи (9.7), маємо

.

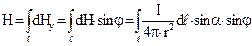Кут α між вектором та 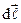дорівнює 90^о; ; .

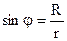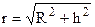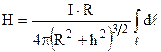. Так як 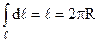є довжина кола, одержуємо

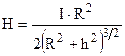і . (9.9)

У центрі колового струму при h = 0 одержуємо

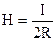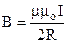; . (9.10)

9.4 Застосування закону Біо-Савара-Лапласа і принципу суперпозиції для розрахунку

магнітного поля прямолінійного провідника зі струмом

Положення точки відносно прямолінійного провідника задамо перпендикуляром r_o до нього (рис.9.7). Очевидно, що вектори 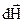від усіх елементів 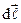провідника однаково направлені. Вони перпендикулярні до площини, в якій лежать провідник 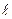і перпендикуляр r_o. Тому вектори 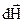будемо додавати алгебраїчно. Маємо 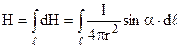. (9.11)

Із рисунка видно, що ; 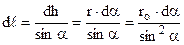. Підстановка в (9.11) після скорочень дає 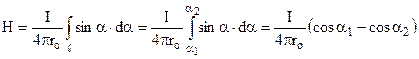. Тут α₁ і α₂ – кути, під якими видно провідник із точки, в якій розраховується напруженість. Таким чином, для прямолінійного провідника зі струмом маємо

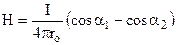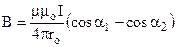; . (9.12)

Для прямолінійного нескінченного провідника α₁ = 0^о; α₂ = 180^о. Одержуємо 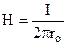; 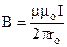. (9.13)

9.5 Взаємодія паралельних прямолінійних провідників із струмом

Розглянемо взаємодію двох нескінченних паралельних прямолінійних провідників із струмами І₁ і І₂, які знаходяться на відстані r_o один від одного. Така взаємодія відбувається через магнітне поле: кожний провідник створює магнітне поле (9.13), яке потім діє на інший провідник (рис.9.8) з силою Ампера (9.1).

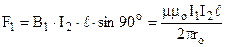. (9.14)

Користуючись правилом правого гвинта та правилом лівої руки, можна впевнитись, що протилежно направлені струми відштовхуються (рис.9.8,а), а однаково направлені – притягуються (рис.9.8,б). Вираз

(9.14) дає можливість означити одиницю струму в 1А. При І₁ = І₂ =1А, r_o = 1м, μ = 1, μ_о = 4∙π∙10^-7 Гн/м, ℓ = 1м, одержуємо F = 2∙10^-7 Н.

9.6 Магнітне поле соленоїда

Соленоїд – це циліндрична котушка з великою кількістю витків N. Осьовий переріз соленоїда показаний на рис.9.9: R - радіус витків, ℓ - довжина котушки. Знайдемо напруженість магнітного поля в деякій точці А на осі соленоїда. Згідно з принципом суперпозиції результуюча напруженість є результатом складання магнітних полів окремих витків (колових струмів). Виберемо на відстані h від точки А нескінченно малий елемент соленоїда довжиною dh. На цей елемент припадає 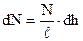витків, кожний із яких створює напруженість (9.9) 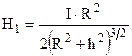.Тоді

.

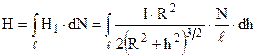Виразимо h і dh через радіус R і кут α. , , .

Після підстановок і спрощень маємо

.

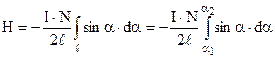Тут α₁ і α₂ – кути, під якими видно кінці соленоїда із точки, в якій розраховується напруженість. Таким чином одержуємо

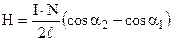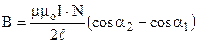; . (9.15)

Для довгого соленоїда, тобто коли R<<ℓ, α₁ =180^о; α₂ = 0^о,

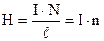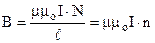; . (9.16)

Тут n - лінійна густина намотки, тобто кількість витків на одиниці довжини соленоїда. Напруженість дорівнює кількості ампер-витків на одиниці довжини. Напрямок векторів визначається за правилом правого гвинта (див. розд.9.3).

9.7 Дія магнітного поля на рухомий заряд (сила Лоренца). Рух заряду в магнітному полі

Сила Лоренца 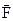– це сила, яка діє на рухомий заряд q у магнітному полі індукцією . Знайдемо її через силу Ампера (9.3). Її можна розглядати як рівнодіючу сил Лоренца, що діють на всі заряди провідника, які мають певну швидкість направленого руху .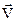

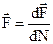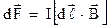; . Струм І запишемо із (8.3) і (8.6) 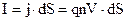. Кількість зарядів . Одержуємо

.

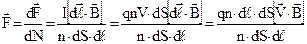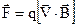, або в скалярній формі 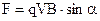. (9.17)

При α = 0^о сила F = 0. На заряд, що летить вздовж магнітного поля воно не діє.

Напрямок сили Лоренца визначається, як і сила Ампера, за правилом лівої руки. Слід звернути увагу, що чотири пальці потрібно направляти по напрямку струму, а не по швидкості заряду. Якщо заряд негативний, то чотири пальці направляють проти швидкості.

Вияснимо, як буде рухатись заряд у магнітному полі? Сила Лоренца перпендикулярна до швидкості, а тому змінює тільки її напрямок і не змінює величину. Тому рух буде рівномірним. Нехай від’ємний заряд q масою m влітає зі швидкістю V у магнітне поле індукцією B перпендикулярно до силових ліній (рис.9.10). Силові лінії направимо перпендикулярно до площини рисунка на нас. Тоді траєкторія буде зображатись у площині рисунка і буде уявляти собою коло радіусом R. Сила Лоренца надає тілу нормального (доцентрового) прискорення. Із другого закону Ньютона маємо . Відомо (2.7), що 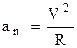. Прирівнюємо праві частини і знаходимо радіус обертання 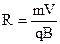. (9.18)

Знайдемо період Т обертання, тобто час одного оберту,

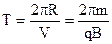. (9.19)

Вираз (9.19) показує, що період не залежить від швидкості руху.

Нехай заряд влітає під кутом φ до напрямку магнітного поля (рис.9.11). Розкладемо швидкість на дві складові: - перпендикулярну до індукції і - паралельну їй. Частинка буде одночасно приймати участь у двох рухах: 1) по колу в перпендикулярній до магнітного поля площині; 2) прямолінійному рівномірному вздовж поля. Отже частинка буде рухатись по гвинтовій лінії радіусом 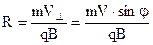(9.20)

з періодом 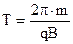(9.21)

і шагом 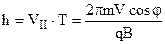. (9.22)

9.8 Циркуляція вектора напруженості магнітного поля. Закон повного струму. Магнітний потік. Теорема Остроградського-

Гаусса для магнітного поля

Криволінійний інтеграл виду 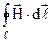називається циркуляцією вектора, в даному випадку напруженості магнітного поля. Знайдемо її значення на прикладі магнітного поля, створеного прямолінійним нескінченним провідником із струмом І. Виберемо довільний замкнутий контур ℓ, який охоплює провідник (рис.9.12). Враховуючи(9.13) і , одержимо

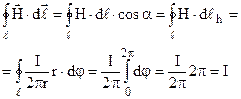
У загальному випадку 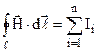(9.23)

Циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі струмів, які охоплює цей контур. Це співвідношення називають законом повного струму. В (9.23) струми, напрямок яких співпадає з поступальним рухом правого гвинта, який обертається в напрямку обходу контура, беруться зі знаком (+), а протилежні - зі знаком (-). Слід зауважити, що форма контура ℓ може бути довільною.

Той факт, що циркуляція вектора напруженості магнітного

поля відмінна від нуля , свідчить, що магнітне поле не потенціальне, а вихрове.

Застосуємо закон повного струму (9.23) для розрахунку магнітного поля.

Приклад 1. Поле прямолінійного нескінченного провідника зі струмом.

Так як форма контура не має значення, виберемо його у формі кола, площина якого перпендикулярна до провідника, а центр співпадає із провідником (рис.9.13). Це дає право вважати, що величина век тора напруженості у всіх точках контура однакова, а кут між вектором напруженості і вектором 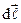дорівнює 0^о. Тому маємо 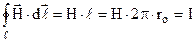. Звідки одержуємо відому формулу (9.13) .

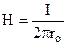Приклад 2.Поле довгого соленоїда. Виберемо контур ℓ у формі прямокутника рис.9.14. Будемо нехтувати крайовими ефектами, тобто будемо вважати, що магнітне поле зосереджене всередині котушки, а за її межами напруженість дорівнює нулю.

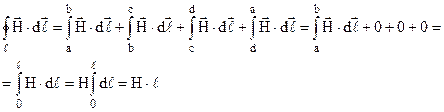Сума струмів дорівнює 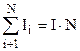. Одержуємо .

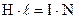Отже напруженість 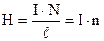, а індукція

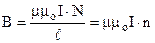, як і по формулам (9.16).

Приклад 3. Поле тороїда. Тороїд – це котушка, намотана на тороїдальне осердя (бублик) (рис.9.15,а). Переріз тороїда показаний на рис.9.15,б. Розрахуємо напруженість магнітного поля для трьох областей: 1) всередині осердя; 2) в осерді; 3) зовні за межами осердя. Виберемо в кожній області кільцевий контур ℓ радіусом r і запишемо для кожного із них закон повного струму (9.23).

а). r < R₁. , так як в контур не потрапляє ні один виток із струмом. Отже Н₁ = 0.

б). R₁ < r₂ < R₂. ; .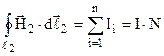

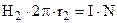в). r₃ > R₂.

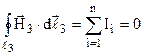, тому що контур ℓ₃ охоплює однакову кількість витків з протилежно направленими струмами.

Таким чином, за межами осердя поле відсутнє, а всередині осердя

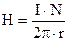. (9.24)

В теорії магнетизму, так же, як і в електростатиці, вводиться поняття потоку вектора індукції (рис. 9.16)

. (9.25)

В_n – проекція вектора індукції на перпендикуляр до площадки. Вимірюється потік у веберах

На відміну від потоку вектора електростатичної індукції через замкнуту поверхню, який, як відомо (7.14), дорівнює алгебраїчній сумі зарядів, потік вектора індукції магнітного поля через довільну замкнуту поверхню дорівнює нулю

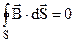. (9.26)

Це є теорема Остроградського Гауса для магнітного поля. Оськільки лінії індукції магнітного поля замкнуті, то число ліній індукції, які входять у замкнуту поверхню, дорівнює числу ліній, які виходять з цієї поверхні. Рівність нулю потіку вектора індукції магнітного поля через довільну замкнуту поверхню означає, щоі в природі не існує уособлених джерел північного, або південного полюсів магніту.

9.9 Контур із струмом у магнітному полі

На елементи контура із струмом у магнітному полі діють сили Ампера, які приводять до повороту контура, його деформації і поступального руху. Розглянемо спочатку поводження прямокутного контура розмірами а·b в однорідному магнітному полі індукцією В (рис.9.17). Сили Ампера 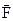, що діють на сторони b, утворюють пару сил. Момент М цієї пари сил (4.37)

повертає контур так, щоб вектор магнітного моменту контура

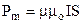(9.27)

співпав з вектором індукції. Вектор Р_m направлений перпендикулярно до площини контура у відповідності з правилом правого гвинта. У векторній формі 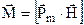. (9.28)

Другими словами, контур повертається в таке положення, щоб магнітний потік через його площу був максимальним. У цьому положенні площина контура перпендикулярна до магнітного поля, а сили Ампера розтягують контур (рис.9.18).

У неоднорідному магнітному полі, коли силові лінії індукції не паралельні, виникає рівнодіюча сил Ампера, направлена вздовж поля (рис.9.19). Пара сил F_┴ обертає контур, а сили F_II рухаютьйого поступально вздовж поля.

9.10 Механічна робота в магнітному полі

Знайдемо роботу dA по переміщенню елемента провідника dℓ із струмом І у магнітному полі індукцією В. Сила Ампера 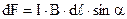переміщує провідник на відстань dx (рис.9.20). Враховуючи (9.1) і (9.25), знайдемо роботу

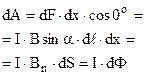
Одержуємо

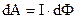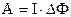, , (9.29)

що робота по переміщенню провідника зі струмом у магнітному полі дорівнює добуткові струму на магнітний потік через площу, яку описує провідник при своєму рухові. Перевіримо розмірність

.

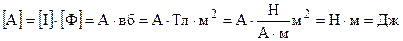Знайдемо роботу по переміщенню замкнутого контура зі струмом. Розіб’ємо контур на дві частини (рис.9.21): ліву abc і праву сda. Нехай контур перемістився в положення a₁b₁c₁d₁. Позначимо початкову площу контура S₁, кінцеву S₂, а фігури сс₁b₁a₁ad – S₀. Роботу по переміщенню контура знайдемо як алгебраїчну суму робіт по переміщенню його частин, скориставшись формулою (9.29). Врахуємо, що при вибраному напрямку струму і магнітного поля сили Ампера, які діють на частину abc утворюють з напрямком переміщення тупі кути. Тому ця робота буде від’ємною. Робота по переміщенню частини cda позитивна. Одержуємо

.

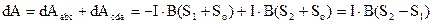Робота 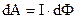, або 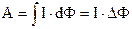(9.30)

дорівнює добуткові струму на зміну магнітного потоку через площу контура.

Якщо маємо не один виток, а котушку з N витками, то робота буде в N разів більшою.

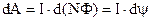
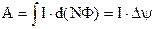(9.31)

Добуток магнітного потоку Ф на кількість витків N називається потокозчепленням 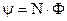. (9.32)

9.11 Явище електромагнітної індукції. Закони Фарадея і Ленца

Явище електромагнітної індукції було відкрите англійським фізиком М.Фарадеєм(1791-1867) у 1821 році і заключається у виникненні електрорушійної сили і індукційного струму в замкнутому контурі при зміні магнітного потоку через площу, обмежену цим контуром. Величина е.р.с. дорівнює швидкості зміни магнітного потоку – це закон Фарадея

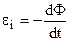, а якщо N витків . (9.33)

Знак (–) відображає правило (закон) Ленца про напрямок індукційного струму. Індукційний струм має такий напрямок, щоб своїм магнітним полем протидіяти зміні основного магнітного поля. Це зовсім не означає, що магнітне поле індукційного струму протилежне основному. Якщо потік зовнішнього поля зростає, поле індукційного струму протилежне йому, якщо ж потік зовнішнього поля зменшується, то магнітне поле індукційного струму співпадає з ним.

Електрорушійна сила виникає і в розімкнутому провіднику, якщо він рухається в магнітному полі. Під дією сили Лоренца 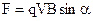вільні електрони зміщуються до одного кінця провідника. Відбувається розділення зарядів (рис.9.22). Виникає електричне поле напруженістю Е, яке діючи на заряд з силою 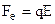, перешкоджає подальшому перерозподілу зарядів. В стаціонарному випадку ці сили рівні між собою 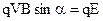. Напруженість 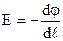. Одержуємо для е.р.с. 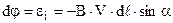. (9.34)

Якщо врахувати, що 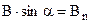, , , , 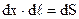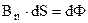одержимо формулу (9.33).

Німецький фізик Г.Гельмгольц (1821-1894) показав, що закон електромагнітної індукції (9.33) можна одержати із закону збереження енергії. Дійсно, нехай по контуру опором R під дією джерела з е.р.с. ε протікає струм І. Контур поміщений у магнітне поле буде рухатись. Робота сторонніх сил 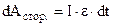витрачається на переміщення контура 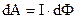і на його нагрівання 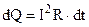. Запишемо закон збереження енергії

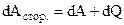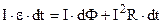; . Знайдемо струм 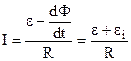. А це не що інше, як закон Ома, де 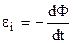є е.р.с. сила індукції (9.33).

9.12 Явище самоіндукції. Індуктивність. Індуктивність соленоїда та

тороїда

При протіканні струму по будь-якому контуру створюється магнітне поле, лінії індукції якого пронизують площу S цього ж самого контура (рис.9.23). Магнітний потік у цьому випадку називається потоком самоіндукції