Рідини. Явища в рідинах 3 страница

У 1853 році два німецьких фізики: Г. Відеман і Р. Франц експериментально встановили закон, який носить їхнє ім’я:

для всіх металів при одній і тій же температурі відношення коефіцієнта теплопровідності 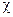до питомої електропровідності σ однакове і пропорційне абсолютній температурі Т

. (8.19)

С – константа, яка не залежить від природи металу.

Розглянемо пояснення цього закону в рамках класичної теорії електропровідності. Коефіцієнт теплопровідності електронного газу, як одноатомного молекулярного газу (6.34) з рахуванням (6.49), дорівнює

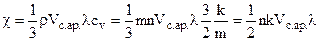
Враховуючи (8.9 ) і (6.25), а також положення про рівність усіх теплових швидкостей електрона (положення 2 розд.8.2), знаходимо відношення

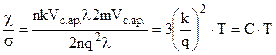. (8.20)

Одержали закон (8.19). Числове значення С_теор=2,23∙10^-8(В/К)² близьке до С_експ= 2,21∙10^-8(В/К)², що підтверджує справедливість теорії.

8.6 Протиріччя класичної теорії електропровідності металів

Досягненням класичної теорії електропровідності металів є те, що вона пояснила такі експериментальні закони: 1) закон Ома; 2) закон Джоуля-Ленца; 3) закон Відемана-Франца. Але ряд експериментальних фактів пояснити не вдалося. Розглянемо ці протиріччя теорії і експерименту.

– Температурна залежність опору металів. По теорії ця залежність визначається (8.10) температурною залежністю середньої арифметичної швидкості електронів (6.24), так як ні концентрація n, ні довжина вільного пробігу λ (див. положення 1, розділ 8.2), а тим більше заряд і маса електрона, не залежать від температури. Таким чином, по теорії 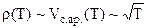(рис.8.7, а).

Експеримент же дає (рис.8.7, б) лінійну залежність

. (8.21)

ρ_о – питомий опір при 0^оС; 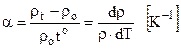- (8.22)

температурний коефіцієнт опору. Він показує відносну зміну опору при зміні температури на 1 градус.

Більш того, при наднизьких температурах у декілька Кельвінів має місце перехід у надпровідний стан (опір різко зменшується до нуля). Класична теорія ніяк не може пояснити це явище.

– Якщо по експериментально виміряному значенню питомого опору порахувати за формулою (8.10) довжину вільного пробігу електрона λ, одержується значення ~ 10^-8м, що на два порядки більше, ніж у положенні 1, розділ 8.2 ~ 10^-10м. Теорія не може пояснити таке дивне поводження електрона в щільно упакованій кристалічній гратці, щоб він пролітав сотню міжатомних відстаней, не стикаючись з іонами.

–Неузгодження з теплоємностями. По класичній теорії теплоємність металів повинна бути більшою, ніж діелектриків, на величину теплоємності електронного газу. Для одного моля ця різниця повинна складати 3/2∙R (див. (6.49)).

Експеримент же дає, що молярна теплоємність при не дуже низьких температурах для всіх твердих тіл (і металів і діелектриків) однакова і дорівнює 3R. Цей закон встановили французькі фізики П. Дюлонг і А. Пті у 1819 році. Пізніше було встановлено, що при низьких і наднизьких температурах теплоємність твердих тіл зменшується до нуля ~ Т³ ( закон П. Дебая, 1912 р.). Класична теорія не може пояснити ці експериментальні факти. Все це спонукало розробку більш досконалої, квантової теорії електропровідності.

8.7 Закони Кірхгофа для розгалужених електричних кіл

Дамо означення декільком понятям електричних схем:

Вузол електричної схеми – це точка, в якій сходяться більше двох провідників.

Вітка – ділянка схеми між двома сусідніми вузлами.

Контур - довільна замкнута дільниця схеми.

Лінійно незалежні контури – це такі, які відрізняються по крайній мірі однією віткою.

Одним із методів розрахунку розгалужених електричних кіл є метод законів Г.Кірхгофа (нім. фізик), сформульованих ним у 1847 р.

Перший закон: алгебраїчна сума струмів у вузлі дорівнює нулю

(8.23)

Струми, які направлені до вузла і від нього, беруться з протилежними знаками (рис.8.8). I₄ + I₃ – I₂ – I₁ = 0

Другий закон: Алгебраїчна сума падінь напруг вздовж будь-якого контуру дорівнює алгебраїчній сумі е.р.с., які увімкнені в цей же контур.

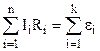(8.24)

У цих сумах знак (+) береться тоді, коли з довільно вибраним напрямком обходу контура співпадає довільно вибраний напрямок струму у вітці, чи напрямок дії е.р.с. В противному випадку береться (–).

Для зображеної схеми (рис.8.9) рівняння 2-го закону Кірхгофа мають вид:

для контура 1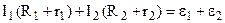

для контура 2 .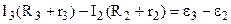

8.8 Робота виходу електронів із металу. Контактна різниця потенціалів (КРП). Закони Вольта

Електрони в провіднику знаходяться в безперервному хаотичному русі з різними тепловими швидкостями. Деякі з них можуть покинути метал і перейти в оточуюче середовище над його поверхнею. Для такого переходу необхідно виконати роботу проти двох сил:

– проти сил відштовхування електронів, які вилетіли раніше і знаходяться в електронній приповерхневій хмарі (рис.8.10);

– проти сил протягування не скомпенсованого позитивного заряду поверхневого шару металу, який утворився внаслідок виходу з нього частини електронів.

Частина електронів покидає метал (перехід 1), а частина повертається (перехід 2). Встановлюється динамічна рівновага між електронною хмарою і металом, коли кількість електронів, які вилітають, дорівнює кількості електронів, що повертаються в метал. При підвищенні температури металу спочатку зросте кількість переходів 1. Але досить швидко зростає і кількість переходів 2. Знову встановиться динамічна рівновага, але вже при більшій густині електронної хмари.

Робота виходу – це робота, яку необхідно затратити для переходу електрона із металу за його межі. Вона різна для різних металів (див табл. 8.1) і лежить в межах 1÷7 еВ (1еВ = 1,6∙10^-19 Дж). Таблиця 8.1

Поверхню металу з електронною хмарою моделюють плоским конденсатором: позитивна пластина – це поверхня металу, негативна – електронна хмара. Для подолання електроном цього затримуючого електричного поля подвійного шару необхідно виконати роботу .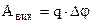

Величина 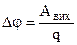(8.25)

називається поверхневим стрибком потенціалу між металом і оточуючим середовищем, або контактною різницею потенціалів (КРП).

Різницю потенціалів на контакті двох різнорідних металів вперше виявив італійський фізик А.Вольта в1799 році. Результати своїх експериментів він узагальнив двома законами:

1-й закон Вольта: при з’єднанні двох різнорідних металів між ними виникає КРП, яка залежить від типу металів і температури контакту;

2-й закон Вольта: КРП на кінцях послідовно з’єднаних різнорідних металів, контакти яких мають однакову температуру, не залежить від проміжних металів і дорівнює КРП при безпосередньому з’єднанні крайніх провідників.

Знайдемо в рамках класичної теорії електропровідності величину КРП між двома металами і перевіримо, чи пояснює вона закони Вольта.

По класичним уявленням КРП зумовлена двома факторами:

–різною роботою виходу електронів із різних металів. Це зовнішня складова КРП ;

–різною об’ємною концентрацією електронів у різних металів. Це внутрішня складова КРП .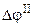

З’ясуємо фізичну природу виникнення кожної із цих складових КРП та знайдемо їх величини.

Нехай маємо два метали з різною роботою виходу електронів, наприклад, А₁ > А₂ (рис.8.11). У цьому випадку при однаковій температурі густина електронної хмари над другим металом буде більшою. Тому після приведення металів у контакт внаслідок дифузії електрони із електронної хмари другого металу будуть переходити в електронну хмару першого металу. Внаслідок таких переходів порушаться динамічні рівноваги електронних хмар над обома металами. Густина електронної хмари над першим металом зростає. Тому зростає кількість електронів, які повертаються в метал 1. Над другим металом густина хмари стала меншою. Для відтворення динамічної рівноваги із металу виходить тепер більше електронів, і він заряджається позитивно. Знайдемо величину . Для цього запишемо роботу по переміщенню електрона вздовж зображеного на рис.8.11 контура, враховуючи, що робота по переміщенню заряду за межами контактного поля дорівнює 0, а також, що загальна робота теж дорівнює 0 (див. розділ 7.4). 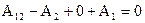. Одержуємо

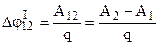. (8.26)

Внутрішня КРП виникає за рахунок переходу електронів із одного металу в інший внаслідок їх дифузії через контакт із областей з більшою концентрацією, наприклад, n₂, в метал з меншою концентрацією n₁ (рис.8.12). Виділимо в граничному шарі контакту нескінченно малий циліндр довжиною dx і площею основи dS. Позначимо концентрацію і „тиск” електронного газу на лівій основі відповідно n і P, а на правій n+dn і P+dP. Зміна електронного „тиску”, у відповідності з основним рівнянням молекулярно-кінетичної теорії (6.14), дорівнює dP = kT∙dn, а сила тиску dF_p = dP∙dS = kT∙dn∙dS. Контактне електричне поле Е буде перешкоджати переходу електронів із 2-го металу в 1-й, тобто на електрони, які знаходяться у вибраному циліндрі, діє електростатична сила dF_E = qEn∙dS∙dx. При встановленні рівноваги dF_p = -dF_E. Одержуємо диференційне рівняння

. Інтегруємо . Права частина у відповідності з (7.27) дає різницю потенціалів

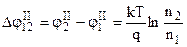. (8.27)

Таким чином, загальна КРП дорівнює

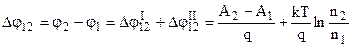. (8.28)

Одержаний вираз показує, що КРП дійсно залежить тільки від хімічного складу металів (робіт виходу та концентрацій електронів) і температури. Це 1-й закон Вольта.

Перевіримо 2-й закон. Для цього знайдемо КРП послідовно з’єднаних, наприклад, чотирьох металів (рис.8.13).

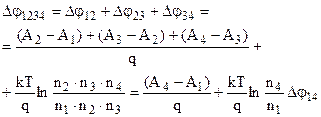
Одержали значення КРП при безпосередньому контакті металів 1 і 4. Отже класична теорія дає і 2-й закон Вольта.

8.9 Термоелектричні явища. Ефекти Зеебека і Пельтьє

Розглянемо замкнуте коло із двох металів 1 і 2 (рис.8.14). В ньому є два контакти: а і б. Нехай температури цих контактів Т_а і Т_б різні. В такому контурі виникає електрорушійна сила, яка називається термо-е.р.с., і протікає електричний струм. Знайдемо термо-е.р.с. ε. Очевидно, що вона буде дорівнювати, у відповідності із 2-м законом Кірхгофа, сумі КРП на контактах. Використаємо (8.28)

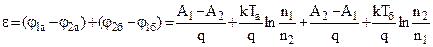
Після спрощень, маємо

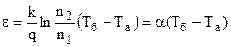. (8.29)

Одержали, що термо-е.р.с. пропорційна різниці температур контактів. Це явище прямого перетворення теплової енергію в електричну називається термоелектричним явищем. Воно було вперше відкрите німецьким фізиком Т.Зеебеком (1770-1831) у 1821 р. на контакті мідь-вісмут. Цей ефект лежить в основі вимірювання температури за допомогою термопар. Першу термопару запропонував і виготовив теж Зеебек. Вона уявляє собою два різних провідники, спаяні одними кінцями, а до інших вмикається гальванометр, яким і вимірюють термо-е.р.с (рис.8.15). Термопару попередньо градуюють по відомій різниці температур для знаходження коефіцієнта α термо-е.р.с. По (8.29) знаходять різницю температур, і, знаючи температуру Т_а, де знаходиться гальванометр, можна знайти температуру Т_б другого контакту.

У 1834 р. французький фізик Ж.Пельтьє (1785-1845) виявив протилежний ефект, який був названий його ім’ям. Ефект Пельтьє заключається в тому, що при проходженні струму через контакт різних провідників у контактах крім джоулевого тепла, в залежності від напрямку струму, виділяється чи поглинається додаткове тепло, назване теплом Пельтьє. На відміну від тепла Джоуля-Ленца, яке пропорційне квадрату струму, тепло Пельтьє пропорційне першій степені струму і змінює знак при зміні напрямку струму. Пояснимо механізм виділення цього тепла. Нехай через контакти двох металів від зовнішнього джерела ε пропускається струм I (рис.8.16). Нехай КРП має таку полярність, що метал 1 заряджається відносно металу 2 негативно. Електрони рухаються в контакті а проти контактного поля Е_а і тому ним прискорюються. Ця додаткова кінетичне енергія черпається за рахунок зменшення теплової енергії контакту, і тому він охолоджується. В контакті б електрон гальмується контактним полем Е_б і віддає йому частину кінетичної енергії направленого руху. Контакт б додатково нагрівається. Отже Т_б > Т_а. Таким чином електрон виконує роль переносчика енергії від одного контакту до іншого, а саме від холодного (а) до гарячого (б). А ц вже є не що інше, як холодильна машина. Саме так на контакті вісмут-сурьма Е.Ленц у 1836 році заморозив краплю води.

8.10 Термоелектронна емісія. Струм у вакуумі

Термоелектронна емісія – це явище випускання електронів з поверхні нагрітих тіл. Воно було відкрите у 1883 році американським вченим Т.Едісоном (1847-1931). При підвищенні температури теплова енергія електронів зростає, тому кількість електронів, здатних подолати поверхневий подвійний електричний шар (енергію виходу), зростає. Це явище забезпечує протікання струму в електронних лампах, тобто являється джерелом вільних носіїв заряду для протікання струму у вакуумі. Вивчається це явище на прикладі електронної лампи-діода (рис.8.17). Досліджується вольт-амперні характеристики (рис.8.18). Розглянемо особливості цих характеристик та їх пояснення.

а) При відсутності анодної напруги (U = 0) анодний струм відмінний від нуля (I ≠ 0). Це зумовлено можливістю електронів потрапити на анод за рахунок енергії, яка залишилась після подолання роботи виходу. Тобто електрони після емісії мають деяку початкову швидкість. Ясно, що із зростання температури катода цей струм теж зростає (див.рис.8.18, криві Т₁ і Т₂).

б) При деякій напрузі струм перестає зростати і виходить на насичення. Це зумовлене тим, що при великих напруженостях прискорюючого електричного поля всі емітовані електрони потрапляють на анод. При підвищенні температури катода його емісійна здатність зростає, і струм насичення теж зростає. Залежність густини струму насичення від температури катода була одержана Річардсоном і Дешманом

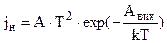. (8.30)

Стала А = 120 А/(см²∙К) однакова для всіх металів. Досліджуючи залежність (8.30), можна визначити роботу виходу.

в) Для того, щоб струм зник, потрібно на анод подати затримуючу напругу (на анод -, на катод +). Ясно, що чим більшою буде температура катода, тим з більшою швидкістю його будуть покидати електрони, тим більшу потрібно затримуючу напругу, щоб робота затримуючого поля була не меншою, ніж максимальна кінетична енергія випущених електронів .

г) С.А.Богуславський (1883-1923, рос. фізик) і І. Ленгмюр (1881-1957, амер. фізик) у 1913р. показали, що зростання анодного струму пропорційне анодній напрузі в степені 3/2

. (8.31)

Це закон Богуславського-Ленгмюра, або його ще називають законом „степені три других”

8.11 Струм у газах

Процес протікання струму в газах називається газовим розрядом. Його існування можливе при наявності вільних носіїв заряду, тобто необхідна їх генерація. В газах носіями струму є електрони і іони, як позитивні, так і негативні. Створити (генерувати) вільні заряди можна: а) дією зовнішнього іонізатора: рентгенівські промені, α,β,γ-випромінювання, космічні промені, нагрівання і т. д. Під дією зовнішнього генератора молекули розпадаються на іони і електрони, якщо для цього виконані енергетичні умови.

б) за рахунок процесу ударної іонізації. Наявні заряди під дією прикладеного електричного поля на довжині свого вільного пробігу набирають енергію, достатню для іонізації нейтральних молекул газу при зіткненні (ударі) з ними.

Наряду з генерацією іде і зворотній процес рекомбінації іонів.

Розряд, який відбувається під дією зовнішнього генератора називається несамостійним, а без нього – самостійним. Типова вольт-амперна характеристика газового розряду, досліджена по схемі рис.8.19, представлена на рис.8 20. В області несамостійного розряду характерні дві дільниці: початкова, майже лінійна, коли виконується закон Ома, і горизонтальна, насичення, коли всі генеровані іони досягають електродів. При вимиканні генератора розряд припиняється після рекомбінації всіх зарядів. При деякій напрузі U_c несамостійний розряд переходить у самостійний. Тепер носії струму генеруються за рахунок процесу ударної іонізації і за рахунок термоелектронної емісії із катода при його нагріванні за рахунок бомбардування позитивними іонами. Розряд підтримується без зовнішнього генератора.

Розрізняють чотири типи самостійних газових розрядів: тліючий, коронний, іскровий і дуговий.

Тліючий розряд виникає у газі за зниженого тиску ( 15–1500 Па) і не дуже високої напруги (200–500 В). Вільні заряди генеруються за рахунок бомбардування катода позитивними іонами і фотонами, які утворюються в газі, а також за рахунок ударної іонізації. Структура цього розряду показана на рис. 8.21.

Безпосередньо до катоду примикає 1- астоновий темний простір (Астон вперше звернув на нього увагу), де електрони, випущені із катоду, ще не встигли набрати швидкості достатньої для збудження атомів і молекул. Ширина цього простору декілька десятих міліметра. Далі іде катодний шар 2, де відбувається збудження атомів і молекул, але ще не іонізація. Повертаючись у нормальний стан, молекули і атоми випромінюють кванти світла. За катодним шаром іде темній катодний простір 3, де починається ударна іонізація і зростання електронних лавин. Саме тут виникають позитивні іони, які і бомбардують катод. Потім формується негативне тліюче свічення 4 зумовлене виділенням енергії рекомбінації електронів з позитивними іонами. Область 5 називається темний простір Фарадея, куди уже електрони не долітають. Потім формується світний стовп 6 – це сукупність іонів протилежних знаків, або холодна плазма. Тут ідуть в основному процеси рекомбінації. Прикладена до електродів напруга в основному падає на перших трьох областях.

Іскровий розряд виникає при атмосферному тиску при високій напруженості електричного поля (для повітря за нормальних умов Е = 3∙10⁶ В/м). Він характеризується перервною структурою навіть при використанні джерела постійного струму. В природі – це блискавка. Зовнішній вид цього розряду (рис.8.22) уявляє собою сніп яскравих зигзагоподібних тонких каналів, які швидко заповнюють розрядний простір, змінюючи один одного. За рахунок ударної іонізації утворюються електропровідні канали іонізованого газу, які називаються стримерами. Стримери виникають, зливаються, розгалужуються, продовжують один одного і таким чином відбувається досить швидке перенесення заряду між електродами (10^-7 ÷ 10^-8с).

Дуговий розряд виникає при великих потужностях джерела живлення, коли стримери зливаються в один електропровідний канал. Дуговий розряд підтримується в основному за рахунок термоелектронної емісії з поверхні катода, який нагрівається до 3000^оС ÷ 4000^оС за рахунок бомбардування його позитивними іонами. Наряду з цим іде і іонізація газу в розрядному проміжку.

Коронний розряд виникає при відносно високому тискові газу, як правило при атмосферному, в сильно неоднорідному електричному полі поблизу великої кривизни поверхні електродів. Напруженість поля сягає 3∙10⁶ В/м. Корона може виникати як на негативному, так і на позитивному електродах.

У випадку негативної корони електрони прискорюються електричним полем поблизу катода і іонізують молекули газу. Позитивні іони бомбардують катод і вибивають з нього електрони. Це явище вторинної електронної емісії. По мірі віддалення від катода напруженість поля падає і електронні лавини обриваються.

В позитивній короні електронні лавини, які іонізують молекули, зароджуються в результаті об’ємної іонізації газу фотонами, які випромінюються короною. Прискорюючись до аноду, електрони іонізують газ.

9 Електромагнетизм

9.1 Магнітне поле рухомих зарядів. Індукція магнітного поля.

Закон Ампера

У 1820 році датський фізик Г.Ерстед (1777-1851) виявив, що поблизу провідників із струмом магнітна стрілка зазнає орієнтуючої дії, тобто струм утворює магнітне поле. Так як струм – це направлений рух зарядів, постали питання: чи всякий рухомий заряд утворює магнітне поле, чи тільки вільні заряди? Яка роль іонів кристалічної гратки?

На перше питання відповів російський фізик А.А.Ейхенвальд (1864-1944). Він у 1901 році провів дослід по виявленню магнітного поля поблизу конвекційного струму (рис.9.1). Заряджений диск приводився в обертання. Виявилось, що незалежно від знаку заряду, а також від того, металевий а) чи діелектричний б) диск, магнітна стрілка поблизу них орієнтувалась певним чином. Причому, коли диски не обертались, орієнтуючий ефект був відсутній. Але роль кристалічної гратки цими дослідами не була вияснена.

У 1911 році російський академік А.Ф.Іоффе (1880-1960) виявив магнітне поле, створене пучком електронів (рис.9.2). Тепер електрони рухались не в кристалічній гратці, а у вакуумі.

Отже, всякий рухомий заряд утворює магнітне поле.

Орієнтація магнітної стрілки у магнітному полі певним чином свідчить про те, що магнітному полю властивий напрямок, а силові його характеристики ( індукція 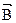, напруженість 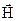)- величини векторні. За напрямок магнітного поля прийнятий напрямок, який вказує північний полюс магнітної стрілки. Графічно магнітне поле зображається лініями індукції, це лінії, дотичні до яких у кожній точці співпадають з вектором індукції (рис.9.3). Досліди показали, що лінії індукції завжди замкнуті. Для прямолінійного провідника зі струмом напрямок силових ліній можна визначити за правилом правого гвинта: коли поступальний рух правого гвинта співпадає зі струмом, напрямок його обертання вказує напрямок ліній індукції.

Взаємодію магнітного поля і провідників із струмом детально вивчав французький фізик А.Ампер (1775-1836). Він у 1820 році встановив, що сила, яка діє на провідник із струмом прямо пропорційна величині струму, довжині провідника і синусу кута між струмом і напрямком магнітного поля (рис.9.4) і направлена перпендикулярно до провідника і магнітного поля 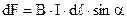. (9.1)

Сила максимальна, коли α = 90^о, тобто коли провідник із струмом перпендикулярний до магнітного поля. Тоді індукція

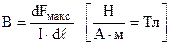(9.2)

чисельно дорівнює силі, що діє на 1м прямолінійного провідника із струмом в 1А, який перпендикулярний до магнітного поля. Вимірюється індукція в системі СІ в теслах (Тл).

Якщо довжину провідника розглядати як вектор, напрямок якого співпадає із напрямком струму, то закон Ампера (9.1) записують у векторній формі

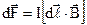. (9.3)

Напрямок сили Ампера можна визначити за правилом лівої руки: якщо ліву руку розмістити так, щоб силові лінії входили в долоню, чотири витягнутих пальці направити по струму, то відігнутий великий палець вкаже напрямок сили.

9.2 Закон Біо-Савара-Лапласа. Принцип суперпозиції для магнітного поля

Закон трьох французьких вчених Біо(1774-1862), Савара(1791-1841) і Лапласа(1749-1827) – це експериментальний закон, який визначає індукцію 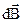магнітного поля, створеного елементом провідника довжиною 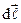із струмом I в точці, віддаленій від цього елементу на відстань (рис.9.5)