Построение ЛВ усилий фермы

Рассмотрим ферму (рис. 5.6 а). При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки (рис. 5.6 б). Поэтому ЛВ опорных реакций фермы будут аналогичны ЛВ балки (рис. 5.6 в, г).

Для построения ЛВ продольных усилий фермы воспользуемся способами вырезания узлов и сквозных сечений.

а) Использование способа вырезания узлов

Для построения ЛВ N_2-6 вначале рассмотрим узел 1. Так как к этому узлу силы не приложены, то по признаку 1 N_1-6=0.

После этого вырежем узел 6 фермы. Здесь могут быть два случая:

1) когда единичная сила P=1 находится в этом узле (рис. 5.6 е), то

SY= N_2-6 sina+1–1=0. Отсюда N_2-6=0.

2) когда единичная сила P=1 находится вне этого узла (рис. 5.6 ж), то

SY=N_2-6 sina+R_A=0. Отсюда N_2-6= – 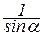×R_A.

Тогда, используя ЛВ опорной реакции R_A, можно построить ЛВ усилия N_2-6 (рис. 5.6 д).

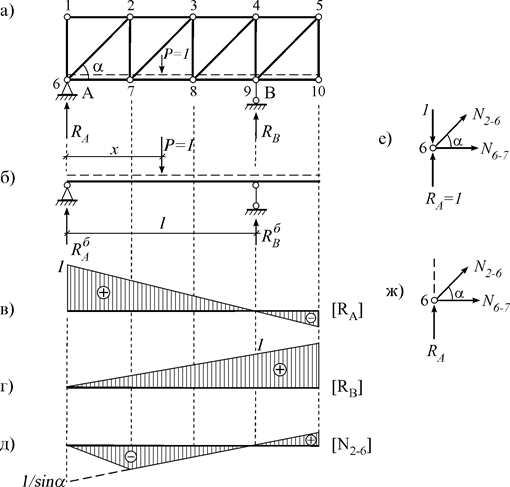
Рис. 5.6

б) Использование способа сквозных сечений

Поперек фермы проведем сквозное сечение I–I (рис. 5.7 а) и получим независимые левые и правые части. Единичная сила P=1 может находиться в обоих частях фермы.

1)Единичная сила левее сечения(рис. 5.7 б):

SM 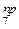=N_2-3 h+R_B 2a=0. Отсюда N_2-3= –2 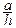R_B ;

SY 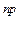= –N_3-7 sina+R_B=0. Отсюда N_3-7= 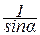R_B .

2)Единичная сила правее сечения (рис. 5.7 в):

SM 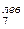= –N_2-3 h – R_A a=0. Отсюда N_2-3= – 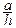R_A ;

SY 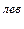=N_3-7 sina+R_A=0. Отсюда N_3-7= – 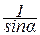R_A .

В первом случае определяем ординаты ЛВ этих усилий между узлами 6-7, т.е. определяем их левые ветви, а во втором случае определяем ординаты обоих ЛВ между узлами 8-10, т.е. определяем правые ветви ЛВ. Соединив точки между узлами 7-8, получаем переходную прямую и окончательный вид ЛВ (рис. 5.7 г, д ).

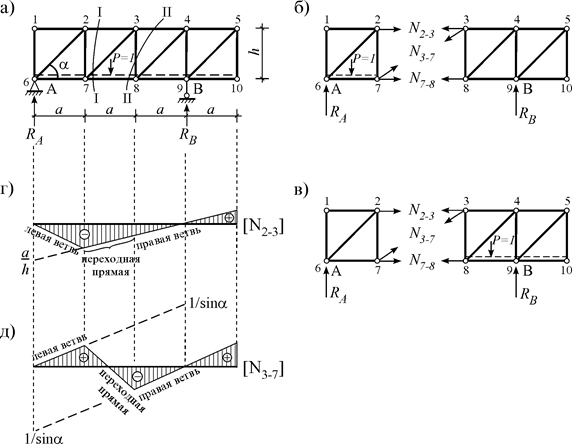
Рис. 5.7

Как видно из этих примеров, у ЛВ продольных усилий фермы есть следующее свойства: ветви ЛВ пересекаются под моментной точкой; если же моментной точки нет, ветви ЛВ параллельны.