Расчет ферм

Ферма – это геометрически неизменяемая система, состоящая из прямых стержней, соединенных в узлах жестко или шарнирно (рис. 4.1 а). Замена жестких узлов шарнирами превращает их в шарнирную ферму (рис. 4.1 б).

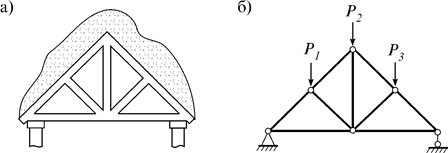
Рис. 4.1

Для статической определимости и геометрической неизменяемости шарнирных ферм должно выполняться условие

.

При действии узловой нагрузки стержни фермы работают в основном на растяжение или сжатие, а моменты и поперечные силы в них отсутствуют. Поэтому в стержнях шарнирной фермы определяются только продольные усилия.

Положительное усилие N_ij в стержне фермы между узлами i и j (рис. 4.2 а) следует направить в сторону от шарниров (рис. 4.2 б).

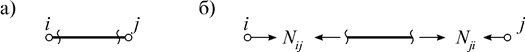
Рис. 4.2

При расчете простых ферм используются методы вырезания узлов, сквозных сечений, совместных сечений, замены стержней и др. Здесь рассмотрим только два метода.

Метод вырезания узлов основан на последовательном вырезании и рассмотрении равновесия узлов фермы.

Сущность метода: вырезается узел, в котором не более двух неизвестных; составляются уравнения равновесия SX=0 и SY=0; из них определяются неизвестные продольные усилия. После этого можно вырезать следующий узел и продолжить расчет.

В методе вырезания узлов необходимо установить порядок вырезания узлов. Например, для расчета фермы (рис. 4.3 а) сначала вырежем узел A (рис. 4.3 б) и запишем уравнения равновесия:

SX = N_A-10+N_A-1 cosa=0;

SY = N_A-1 sina+1,5P=0.

Из них: N_A-1= –1,5P/sina; N_A-10=1,5P/tga .

Рис. 4.3

Теперь вырежем узел 10 (рис. 4.3 в) и запишем условия равновесия:

SX = N_9-10 –N_A-10=0;

SY = N_1-10=0.

Из них получаем: N_9-10 =N_A-10=1,5P/tga; N_1-10=0.

После этого можно вырезать узлы 1, 9, 2, 3, 8, 4, 7, 6, 5.

У метода вырезания узлов есть недостаток: ошибка (неточность), допущенная при расчете одного узла, влияет на последующие вычисления. Поэтому результаты, полученные этим методом, надо контролировать. Например, результаты расчета фермы могут быть проверены по формуле

,

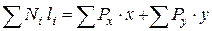где 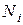– усилия в стержнях, – длины стержней, и 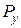– проекции нагрузок (включая и опорные реакции), x и y – координаты нагрузок.

Из метода вырезания узлов вытекают несколько признаков (частных случаев), упрощающих расчет ферм:

1) если в узле сходятся два стержня и внешняя нагрузка не приложена (рис. 4.4 а), то оба усилия равны нулю: N₁= N₂=0;

2) если в узле сходятся два стержня, а внешняя нагрузка действует в направлении одного стержня (рис. 4.4 б), то N₁=P, N₂=0;

3) если в трехстержневом узле два стержня лежат на одной прямой, а внешней нагрузки нет (рис. 4.4 в), то усилия в двух стержнях равны: N₁= N₂, а усилие в боковом стержне равно нулю: N₃=0;

4) если в четырехстержневом узле стержни попарно лежат на одной прямой, а внешней нагрузки нет (рис. 4.4 г), то усилия также попарно равны между собой: N₁= N₂, N₃= N₄.

Рис. 4.4

Используя эти признаки легко определяются некоторые усилия рассмотренной фермы (рис. 4.3 а):

– по 2-му признаку N_1-10=N_1-9=N_2-9=0; N_5-6=N_5-7=N_4-7=0;

– по 3-му признаку N_A-10=N_9-10=N_8-9; N_B-6=N_6-7=N_7-8; N_A-1=N_1-2; N_B-5= N_4-5.

Метод сквозных сечений позволяет определять усилие в стержне фермы только из одного уравнения.

Сущность метода: поперек фермы проводится такое сквозное сечение, чтобы появилось не более трех неизвестных усилий; в точке пересечения направлений двух из них составляется уравнение момента, из которого определяется третье усилие.

Точка, в которой составляется уравнение момента, называется моментной точкой.

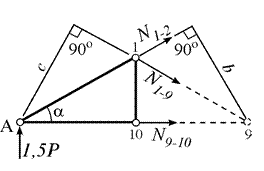В качестве примера рассмотрим ту же ферму, проведя через нее сквозное сечение I–I (рис. 4.3 а). Рассматривая равновесие левой части от сечения (рис. 4.5), составим уравнение момента в точке 1:

SM₁ = N_9-10× 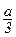–1,5P×a=0.

Отсюда получаем: N_9-10=4,5P . Рис. 4.5

Точка 9 является моментной точкой для N_1-2. Поэтому

SM₉ = –N_1-2 b –1,5P×2a=0.

Так как b=2a×sina, получаем N_1-2=–1,5P/ sina .

Для N_1-9: SM_A = –N_1-9×c=0. Отсюда получаем N_1-9=0.

Иногда (например, когда два стержня параллельны) моментной точки не существует. В этом случае вместо уравнения момента следует составлять уравнение проекции на ось, перпендикулярную этим параллельным стержням.

У метода сквозных сечений есть один недостаток: в сложных фермах не удается провести такое сквозное сечение, чтобы появились только три неизвестных усилия. В этом случае некоторые неизвестные нужно определять заранее или использовать другие методы (методы совместных сечений или замены связей).