Тема №10. Условия работы элементарных ступеней, расположенных на разных радиусах

До сих пор при рассмотрении процессов в ступени предполагалось, что параметры потока в зазорах между соплами и рабочими лопатками, перед и за ступенью неизменны вдоль радиуса, т.е. 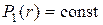, , 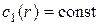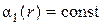и т.д. Однако во всякой реальной ступени параметры потока вдоль радиуса изменяются. Эти изменения сравнительно невелики в ступенях с 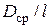>10…13, т.е. для ступеней с относительно короткими лопатками. При их расчете и профилировании изменением параметров по высоте могут иногда пренебрегать. Ступени с 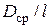<10 относят к ступеням с длинными лопатками (ступени большой веерности). В этих ступенях параметры вдоль радиуса (по высоте лопатки) изменяются значительно, что приводит к необходимости учитывать эти изменения при профилировании. В таких ступенях профили сопловой и рабочей лопаток необходимо изменять по радиусу для учета изменения углов потока на входе в решетки и выходе из них, т.е. лопатки приходится «закручивать», чтобы обеспечить высокий КПД ступени.

Таким образом, в детальных расчетах необходимо учитывать изменение параметров потока по высоте лопаток, т. к. для высокого КПД ступени форма лопаток должна соответствовать треугольникам скоростей (кинематическим параметрам потока) на различных радиусах.

Окружная скорость лопаток РК линейно возрастает от корня к периферии 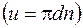. Изменение абсолютных и относительных скоростей потока происходит по более сложным законам, в которых существенную роль играет изменение давления воздуха под действием ЦБС.

Проходя НА, поток воздуха получает закрутку вокруг оси колеса. При этом возникает ЦБС, которые повышают давление воздуха в периферийных сечениях (рис. 10.1). Повышение же давления, согласно уравнению Бернулли ( 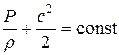) приводит к снижению скорости потока.

Реальное течение воздуха в ОК является прос-транственным периодически неустановившимся течением вязкого сжимаемого газа, математическое исследование которого в строгой постановке затруднительно. По этой причине делают некоторые допущения:

1) рассматривают осредненные значения параметров в точке (стационарность);

2) во всех сечениях каждой ступени неизменными.

Рассмотрим при этих условиях течение воздуха в осевом зазоре между СА и РК.

Выделим в пределах зазора элементарный объем, ограниченный цилиндрическими поверхностями с радиусам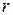и и 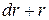, двумя плоскостями, проходящими через ось симметрии ступени и расположенными под углом 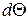друг к другу, и двумя нормальными к оси плоскостями, расположенными на расстоянии 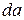(см. рис. 10.2).

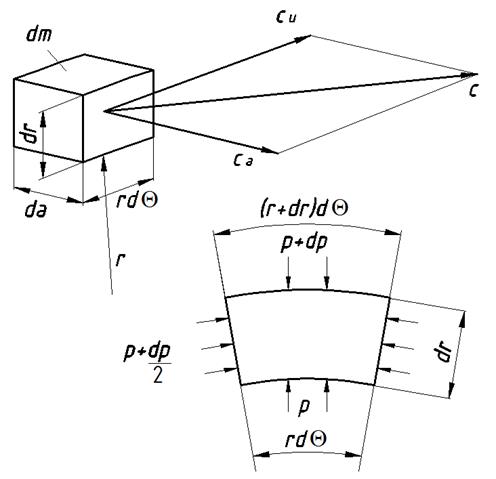
Рис. 10.2. К выводу уравнения радиального равновесия потока в ступени

Абсолютную скорость разложим на составляющие 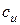и .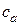

Сумма всех сил, действующих на объем, как известно, должна быть равна нулю. Запишем это равновесие для радиальной составляющей:

- центробежная сила, действующая на элементарный объем, будет равна 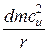(где 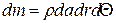- масса воздуха, заключенного в объеме);

- силовое воздействие на поток отсутствует;

- внешние силы – это силы давления.

Можно записать условие радиального равновесия (сокращенное на ):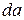

.

Или, после некоторых преобразований:

.

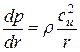Это уравнение получило название уравнение радиального равновесия.

Оно является условием равенства ЦБС инерции и сил газодинамических давлений, действующих в радиальном направлении. Оно показывает, что при принятых допущениях градиент давления по радиусу пропорционален квадрату окружной составляющей скорости и обратно пропорционален радиусу.

С учетом уравнения радиального равновесия и того, что 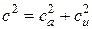, можно записать:

.

Ступени турбомашин часто проектируют так, чтобы 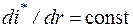. Тогда:

.

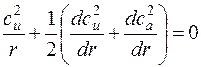Уравнение (2.42) определяет однозначную связь между законами изменения окружной и осевой составляющих скорости воздуха по высоте лопатки перед и за колесом.

Однако одно уравнение не может определить два закона изменения входящих в него величин. По этой причине один из законов выбирают произвольно. Эти законы получили название законов закрутки.