Цена облигаций
В соответствие с Федеральным законом «О рынке ценных бумаг», под облигацией понимается эмиссионная ценная бумага, закрепляющая права ее держателя на получение от эмитента облигации в предусмотренный срок ее номинальной стоимости и зафиксированного в ней процента от этой стоимости.
Облигация имеет номинал (или номинальную цену), эмиссионную цену, курсовую цену, цену погашения.
Номинальная ценанапечатана на бланке облигации и обозначает сумму, которая берется взаймы и подлежит возврату по истечении срока облигационного займа. Она также служит базой для начисления процентов.
Эмиссионная цена облигации — это та цена, по которой происходит продажа облигаций их первым владельцам. Оплата эмиссионных ценных бумаг общества, размещаемых посредством подписки, осуществляется по цене, определяемой советом директоров. Эмиссионная цена может быть равна, меньше или больше номинала.
Цена погашения — это та цена, которая выплачивается владельцам облигаций по окончании срока займа. В большинстве выпусков цена погашения равна номинальной цене, однако она может и отличаться от номинала.
Рыночная цена— это цена, по которой облигация продается и покупается на рынке.
Курс облигации— это значение рыночной цены, выраженное в процентах к ее номиналу.
В соответствие с рассмотренным выше фундаментальным подходом теоретическая стоимость любой ценной бумаги определяется путем приведения к настоящему моменту времени всех доходов, которые планирует получить инвестор за время владения ценной бумагой.
В зависимости от способа выплаты процентного дохода можно выделить два типа облигаций:
а) облигации с периодической платой процентного дохода или купонные облигации
б) бескупонные (или дисконтные) облигации, доход по которым образуется за счет разницы между ценой погашения облигации и эмиссионной ценой и выплачивается при погашении облигации.
Рассмотрим сначала облигацию с периодической выплатой процентного дохода. Доход инвестора от владения такой ценной бумагой складывается из периодических купонных выплат и суммы, равной номиналу при погашении облигации. Исходя из этого формула для определения стоимости облигации может быть представлена в следующем общем виде
P = I/(1+R)1+ I/(1+R)2+ … +I/(1+R)n+ N/(1+R)n = 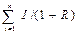 i + N/(1+R)n
i + N/(1+R)n
где Р — цена облигации; I — процентный (купонный) доход в денежных единицах, R — требуемая норма прибыли (ставка дисконтирования). При этом купонный доход определяется как произведение купонной ставки (i) на номинал облигации:
I = i* N.
Для расчета цены облигации может быть также использована полученная ранее формула аннуитета:
P = I/R*[1-1/(1+R)n] + N/(1+R)n.
Пример. Продается облигация номиналом 10000 руб., купонная ставка составляет 12% годовых. Выплата процентов производится один раз в год. До погашения облигации остается ровно 5 лет. Требуемая норма прибыли инвестора составляет 15%. Определить курсовую цену облигации.
По данному типу облигации держатель облигации в конце каждого года получает процентный доход в размере 1200 руб. (10000*0,12), а в конце пятого года кроме этого сумму, равную номиналу облигации т. е. 10000 руб. Определим дисконтированные (приведенные) стоимости для каждого года и найдем их сумму. С учетом этого цена облигации будет равна:
P = I/(1+R)1+ I/(1+R)2+ I/(1+R)3+ I/(1+R)4 + (I+N)/(1+R)5 = 1200/(1+0,15)1 + 1200/(1+0,15)2 +1200/(1+0,15)3 + 1200/(1+0,15)4 +(1200+10000)/(1+0,15)5 =
1043,48+ 907,37 + 789,02 + 686,1 + 5568,38 = 8994,35 руб.
Часто цена облигации выражается в процентном отношении к номиналу. Применительно к приведенному примеру цена облигации составляет 89,94% номинала.
Для приведенного выше примера цена облигации, вычисленная по полученной формуле, составит:
P = 1200/0,15*[1-1/(1+0,15)5] + 10000/(1+0,15)5 = 8994,35 руб.
Таким образом, мы получили тот же результат, что и в предыдущем случае.
В реальных условиях в зависимости от изменения ситуации на финансовом рынке купонная ставка, а также ставка дисконтирования могут изменяться в различные периоды владения облигацией. Стоимость облигации в данном случае определяется из следующей формулы:
P= I1/(1+R1) + I2/[(1+R1)*(1+R2)] + (IN + N)/[(1+R1)*(1+R2)*..(1+Rn)],
где I1, I2, In— процентный доход i-того периода (i = 1, 2, ..., п) R1, R2, Rnтребуемая норма прибыли (ставка дисконтирования) i-того периода. При расчете цены облигации в данном случае необходимо оценить величину процентных выплат и требуемую норму прибыли для всех периодов.
Пример. По облигации номиналом 10000 руб. выплачивается доход в размере 10% годовых. Выплата процентов производится один раз в год. До погашения облигации остается 5 лет. Требуемая норма прибыли в течение первых трех лет (R1) — 15%, четвертый год(R2) — 12, пятый год (R3) — 10%. Определить курсовую цену облигации.
Цена облигации в данном примере может быть определена из следующего выражения:
P = I/(1+R1)1+ I/(1+R1)2 + I/(1+R1)3 + I/[(1+R1)3*(1+R2)]+ (I+N)/[(1+R1)3*(1+R2)* *(1+R3)] = 1000/(1+0,15)1+1000/(1+0,15)2 +1000/(1+0,15)3 +1000/[(1+0,15)3 * (1+0,12)] + (1000+10000)/[(1+0,15)3 * (1+0,12) * (1+0,1)] =
869,57+ 756,14 + 657,52 + 587,07 + 5870,68 =8740,98 руб.
Мы рассмотрели вопрос определения цены облигации при ежегодных купонных выплатах. На практике процентные платежи могут осуществляться чаще, чем один раз в год. Так, например, по облигациям, эмитированным в США, доход часто выплачивается два раза в год. Для определения цены таких облигаций может быть использовано выражение
P = (I/m)/(R/m)*[1-1/(1+R/m)n*m] + N/(1+R/m)n*m ,
где m – число купонных выплат в течение года.
Пример. По облигации, имеющей номинальную цену 1000 рублей и купонную ставку 14%, процентные платежи выплачиваются два раза в год. Необходимо определить цену облигации, если до погашения остается 7 лет и требуемая норма прибыли составляет 16% годовых. Используя представленную выше формулу, получим:
P = (I/m)/(R/m)*[1-1/(1+R/m)n*m] + N/(1+R/m)n*m =
70/0,08*[1-1/(1+0,08)14 ]+ 1000/(1+0,08)14 = 917,56 руб.
Для облигаций, купонные выплаты по которым осуществляются чаще, чем один раз в год может быть рассчитана эффективная процентная ставка с использованием следующего выражения:
iэ = (1+i/m)m -1.
Для предыдущего примера эффективная купонная ставка будет равна
iэ = (1+i/ m)m -1 = (1+0,14/2)2 -1 = 0,145 или 14,5%.
В рассмотренных нами выше примерах до погашения облигации осталось целое число лет или купонных периодов. Однако облигации могут продаваться и покупаются в течение купонного периода. При этом весь купонный доход за этот период получает новый владелец. Между тем часть купонного периода облигация находилась в руках продавца. В связи с этим продавец и покупатель должны разделить купонный доход пропорционально времени владения облигацией в течение общего купонного периода:
I1 = I * T/365,
I2 = I * (365-T)/365
где I — процентный доход за год или купонный период; Т — время, в течение которого облигация находилась в руках продавца (в днях); I1 — процентный доход продавца за время владения (Т); I2 — процентный доход покупателя за время владения (365-Т).
Пример. Продается облигация номиналом 10000 руб., купонная ставка составляет 12% годовых. Выплата процентов производится один раз в год. До погашения облигации остается 4 года и 300 дней. Требуемая норма прибыли инвестора составляет 15%. Определить курсовую цену облигации.
В нашем примере процентный доход покупателя за общий купонный период составит:
D300 = 1200 * 300/365 = 986,3 руб.,
а процентный доход продавца будет равен:
D65 = 1200 * 65/365 = 213,7 руб.
При приобретении облигации в начале купонного периода ее цена составляла 8994,35 руб. Поскольку процентный доход, принадлежащий продавцу, получит покупатель облигации при оплате очередного купона, то цена облигации должна быть увеличена на 213,7 руб. и составить 9208,05 руб.
Рассмотренный подход позволяет получить приближенный результат для цены облигации. Для более точных расчетов нужно продисконтировать ожидаемые доходы за тот период времени, который остается до погашения облигации с момента совершения сделки.
Определим цену облигации для нашего примера:
P = 1200/(1+0,15)300/365+ 1200/(1+0,15)1+300/365+1200/(1+0,15)2+300/365 1200/(1+0,15)3+300/365 (1200+10000)/(1+0,15)4+300/365 = 1021,83+ 930,23+808,89+703,39+ 5708,64 = 9172,98 руб.
Рассмотрим далее задачу определения цены бескупонной облигации. Ее можно представить как купонную облигацию с нулевым размером купонных платежей. Поскольку процентные платежи при этом равны нулю, то рассмотренная ранее формула принимает следующий вид:
P = N/(1+R)n
Пример. Бескупонная облигация номиналом 10000 руб. погашается по номиналу через 3 года. Определить курсовую цену облигации, если ставка дисконтирования составляет 15% годовых.
P = 10000/(1+0,15)3 = 6575,16 руб.
Рассмотренная формула может быть использована и при определении курсовой стоимости краткосрочных ценных бумаг – со сроком действия менее 1 года.
Пример. Определить цену краткосрочной облигации номиналом 1000 руб., погашение через 180 дней. Требуемая норма прибыли по данному типу облигаций составляет 20% годовых.
Используя полученную выше формулу получим:
P = 1000/(1+0,2)180/365= 914,01 руб.
Однако для определения цены краткосрочных облигаций обычно используется приближенная формула:
P = N/(1+R*T/365),
Т — время владения облигацией (в днях).
Применяя эту формулу, получаем:
P = 1000/(1+0,2*180/365)=910,22 руб.
Поскольку величины расхождений расчетной цены, полученной с использованием разных формул, являются весьма незначительными, то при вычислениях с краткосрочными инструментами в большинстве случаев используется приближенная формула.
Риск держателя облигации во многом связан с изменением процентных ставок. В связи с этим рассмотрим зависимость цены облигации от ставки процента (требуемой нормы прибыли R). Цена облигации складывается из дисконтированных купонных выплат и номинала облигации. Из представленной ниже формулы видно, что обе эти величины убывают при повышении процентной ставки R. Исходя из этого, мы можем сделать вывод о влиянии денежно-кредитной политики государства на рыночные цены облигаций.
P = I/R*[1-1/(1+R)n] + N/(1+R)n.
При повышении учетной ставки ЦБ происходит повышение стоимости денежно-кредитных ресурсов в экономике – растут процентные ставки. Соответственно повышаются требования инвесторов к доходности облигаций. Новые облигации эмитируются с большей величиной доходности, а стоимость ранее эмитированных облигаций понижается для обеспечения повысившихся требований к доходности. При снижении учетной ставки ситуации развивается в противоположном направлении.
Пример. Облигация имеет номинал 10000 рублей, купонную ставку 6% и срок погашения 15 лет. Определить размер премии (дисконта), если требуемая норма прибыли составляет 8%.
Найдем цену облигации с использованием следующего выражения
P = I/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)15] + 10000/(1+0,08)15 =
5135,7 + 3152,4 = 8288,1.
Таким образом, в данном случае облигация продается с дисконтом, размер которого составляет 10000 – 8288,1 = 1711,9 руб.
Рассмотрим далее случай, когда требуемая норма прибыли меньше купонной ставки, R = 4%.
P = I/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)15] + 10000/(1+0,04)15 =
6671 + 5553 = 12224.
В данном случае облигация продается с премией, размер которой составляет 2224 руб.
Последний вариант соответствует равенству купонной ставки и нормы прибыли
P = I/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,06*[1-1/(1+0,06)15] + 10000/(1+0,06)15 =
5827 + 4173 = 10000 руб.
Таким образом, мы можем сделать вывод, что при равенстве требуемой нормы прибыли и купонной ставки курсовая цена облигации равна ее номиналу. При превышении нормы прибыли купонной ставки облигация продается с дисконтом, а при понижении относительно купонной ставки – с премией. Цена облигации и требуемая норма прибыли связаны обратной зависимостью. При повышении процентной ставки цена облигации, которая определяется как приведенная стоимость будущих денежных поступлений, падает; при снижении ставок ситуации развивается в противоположном направлении.
Рассмотрим далее влияние фактора времени на стоимость облигации. В предыдущем примере рассмотрим эффект уменьшения срока погашения облигации до 10 лет:
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)10] + 10000/(1+0,08)10 =
4026 + 4632 = 8658 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)10] + 10000/(1+0,04)10 =
4867 + 6756 = 11623 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,06*[1-1/(1+0,06)10] + 10000/(1+0,06)10 =
4416 + 5584 = 1000 руб.
На основе проделанных вычислений мы можем сделать вывод, что при уменьшении срока погашения облигации произошло снижение размера дисконта и премии. При равенстве купонной ставки и нормы прибыли курсовая цена равна номиналу вне зависимости от срока погашения.
Теперь рассмотрим эффект увеличения срока погашения до 20 лет:
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,08*[1-1/(1+0,08)20] + 10000/(1+0,08)20 =
5891 + 2146 = 8037 руб.
P = D/R*[1-1/(1+R)n] + N/(1+R)n = 600/0,04*[1-1/(1+0,04)20] + 10000/(1+0,04)20 =
8154 + 4564 = 12718 руб.
Как и следовало ожидать, при увеличении срока погашения происходит возрастание как величины дисконта, так и премии.
Зависимость цены облигаций от процентной ставки обуславливает риск инвесторов, связанный с ее колебаниями. В связи с этим актуальной является задача анализа чувствительности цены облигации к изменению требуемой нормы прибыли. Выражение для цены облигации может быть представлено в следующем виде:
P = CF1/(1+R)1+ CF2/(1+R)2+ … + CF n/(1+R)n,
где CF i – доход инвестора от владения облигацией в соответствующий период. Для анализа чувствительности цены к процентной ставке необходимо вычислить производную цены по доходности:
dP/dR = (-1)*CF1/(1+R)2+ (-2)*CF2/(1+R)3+ … + (-n)*CF n/(1+R)n+1,
Разделим далее левую и правую части соотношения на цену облигации (Р):
dP/dR * 1/Р= [(-1)*CF1/(1+R)2+ (-2)*CF2/(1+R)3+ … + (-n)*CF n/(1+R)n+1]/P.
Таким образом, мы получили выражение нормализованной по цене облигации чувствительности цены к изменению нормы прибыли. Представленное ниже выражение определяет показатель «дюрации» облигации (D)
D= [(1)*CF1/(1+R)2+ (2)*CF2/(1+R)3+ … + (n)*CF n/(1+R)n+1]/P.
Дюрация характеризует процентный риск облигации, т.е. риск, связанный с изменением процентных ставок. При увеличении значения дюрации возрастает чувствительность цены облигации к изменению процентной ставки и соответственно увеличивается риск ценной бумаги.
Пример. Необходимо рассчитать дюрацию облигации, имеющей номинальную цену 1000 руб., купонную ставку 10% и срок погашения 5 лет. Результаты расчетов сведены в табл. 4.1.
Таблица 4.1
Расчет дюрации облигации
| Номер платежа | Размер платежа CF i | Приведенная величина платежа CF i/(1+R) i | Нормализованная приведенная величина платежа CF i/(1+R) i/Р | Величина i * CF i/(1+R) i/Р |
| 90,91 | 0,09091 | 0,9091 | ||
| 82,64 | 0,08264 | 0,16528 | ||
| 75,13 | 0,07513 | 0,22539 | ||
| 68,3 | 0,06830 | 0,27320 | ||
| 683,02 | 0,68302 | 3,41510 | ||
| Итого | 1,0 | 4,1699 |
Таким образом, величина дюрации для анализируемой облигации составила 4,1699 лет. Дюрацию называют также эффективным сроком жизни облигации. Чем выше этот срок жизни, тем в большей мере облигация реагирует на изменение процентных ставок; иными словами тем она более чувствительна к изменению ставок.
В общем случае чувствительность цены к изменению процентных ставок зависит от времени до погашения облигации и купонной ставки; величина процентного риска возрастает при увеличении времени до погашения и снижении купонной ставки. Обусловлено это тем обстоятельством, что существенная часть цены облигации формируется за счет вклада приведенного значения номинальной цены, которую инвестор получает при погашении облигации. Чем дальше от текущего момента осуществляется эта выплата, тем она больше зависит от изменения процентной ставки. Что касается величины купонной ставки, то ситуация здесь примерно аналогична предыдущему случаю. При снижении купонной ставки повышается та часть цены облигации, которая формируется за счет приведенного значения номинальной цены, что, как было показано выше, приводит к росту процентного риска.
Дата добавления: 2015-06-17; просмотров: 3645;
