Сложные (динамические) методы

Реализация инвестиционных проектов, как правило, предусматривает проведение первоначальных инвестиционных затрат и последующее получение доходов от эксплуатации инвестиций. Таким образом, этапы вложения капитала и получения дохода разделены во времени. В связи с этим для получения верной оценки инвестиционной привлекательности проекта, связанного с долгосрочным вложением денежных средств, необходимо определить, насколько будущие поступления оправдывают сегодняшние затраты. Необходимость оценки денежных средств во времени связана с тем, что стоимость денежных ресурсов с течением времени изменяется. При этом имеется в виду не только обесценивание денежных средств в результате инфляции, но и более фундаментальный аспект, связанный с обращением капитала. Сегодняшний рубль, помещенный в любые коммерческие операции (вложение в ценные бумаги, банковский депозит, инвестиционный проект и т.п.), через определенный период времени может получить приращение за счет дохода.

На практике среди сложных методов наибольшее распространение получили методы, предусматривающие расчет показателей чистой текущей стоимости проекта (NPV), внутренней нормы прибыли (IRR) и рентабельности инвестиций PI.

Чистая текущая (приведенная) стоимость проекта (NPV) – показатель, определяемый как разница между приведенными (дисконтированными) чистыми денежными доходами от инвестиционного проекта и инвестиционными затратами. Экономический смысл данного показателя состоит в том, что он позволяет оценить изменение стоимости компании в результате реализации инвестиционного проекта.

где Cn – чистые денежные поступления от проекта в момент времени n;

Iк – инвестиции в момент времени к;

r – ставка дисконтирования.

Если инвестиционные затраты имеют место только перед началом инвестиционного проекта, то последнее выражение преобразуется к виду:

Таким образом, показатель NPV дает оценку инвестиционных затрат и будущих доходов, приведенных к текущему моменту времени.

Пример. Рассчитать чистую текущую стоимость проекта при следующих условиях:

1. Первоначальные инвестиции составляют 25 млн. руб.

2. Чистая отдача в конце первого года 15 млн. руб., в конце второго года – 10 млн. руб. и третьего года – 8 млн. руб.

3. Ставка дисконтирования – 12%.

NPV=15 /(1+0,12)¹ + 10 / (1+0,12)² +8 / (1+0,12)³ - 25 / (1+0,12)⁰ =2,06 млн. руб.

Чистая текущая стоимость показывает сальдо приведённых к нулевому моменту времени чистых поступлений и инвестиций. Положительное значение NPV означает увеличение стоимости предприятия или увеличение богатства инвестора в результате реализации инвестиционного проекта. Если NPV меньше нуля, то стоимость компании (богатство инвесторов) снижается при реализации проекта и такой проект должен быть отвергнут. В данном примере показатель NPV имеет значение большее нуля и, следовательно, такой проект может быть рекомендован к реализации.

Таким образом, критерием эффективности инвестиционного проекта является условие NPV > 0. При сравнении альтернативных проектов выбирается проект с большей величиной NPV (NPV₁ > NPV₂).

Расчет показателя NPV осуществляется в следующей последовательности:

1) Срок жизни проекта разбивается на временные этапы планирования.

2) Составляется прогноз оттока и притока денежных средств для каждого этапа.

3) Определяется чистый денежный поток.

4) Значения чистого денежного потока дисконтируются.

В настоящее время метод расчета чистой текущей стоимости получил широкое распространение и является одним из стандартных методов, рекомендованных к применению ООН и Всемирным банком. При его применении необходимо рассматривать денежные потоки в рамках инвестиционного проекта изолированно от прочих потоков, т.е. учитывать только платежи и поступления, непосредственно связанные с реализацией данного проекта. Использование метода чистой текущей стоимости предполагает использование следующей информации:

1. Доходы и расходы, связанные с производством и реализацией продукции в рамках инвестиционного проекта для каждого периода реализации проекта.

2. Инвестиционные затраты в рамках проекта.

3. Период реализации проекта.

4. Требуемая норма прибыли (ставка дисконтирования).

Обоснование требуемой нормы прибыли является одной из важнейших проблем при использовании метода NPV. Эта норма должна учитывать как существующую на предприятии или же в отрасли среднюю доходность, так и степень риска проекта. Для предварительных расчетов в качестве нормы прибыли можно использовать процентную ставку по долгосрочным вкладам. При реализации проектов на действующем предприятии ставку дисконтирования целесообразно выбирать исходя из средневзвешенной стоимости капитала фирмы. Определенную таким образом ставку дисконтирования следует рассматривать как минимальный уровень доходности. При расчете NPV, как правило, используется постоянная ставка дисконтирования, однако в зависимости от условий реализации проекта, ставка дисконтирования может дифференцироваться по годам.

Пример. Предприятие планирует закупить новое оборудование стоимостью 20 тыс. руб. Срок его эксплуатации составляет 5 лет и оно имеет нулевую остаточную стоимость. Использование оборудования связано с ростом эксплуатационных издержек на 4 тыс. рублей в год. При этом снижение затрат на оплату труда составляет 10 тыс. руб. Норма прибыли равна 15%. Необходимо рассчитать показатель NPV.

Таким образом, чистые денежные поступления в рамках проекта составляют 6 тыс. рублей в год, а период реализации проекта – 5 лет. Показатель NPV для данного проекта будет равен:

NPV = - I + CF/i*[1-1/(1+i)ⁿ)] = -20 + 6/0,15*[1-1/(1+0,15)⁵] = 113 руб.

Проект имеет показатель NPV близкий к нулю. Формально он может быть принят к реализации, так как NPV>0. Однако проект имеет крайне незначительный запас устойчивости и его реализация связана со значительным риском.

Широкое распространение метода чистой текущей стоимости обусловлено его преимуществами по сравнению с другими методами оценки эффективности инвестиционных проектов. К числу основных относятся учет временной стоимости денег, а также результатов функционирования проекта в течение всего расчетного периода. При этом главным является возможность оценки изменения стоимости фирмы в результате реализации проекта.

Несмотря на все эти преимущества оценки инвестиций, метод чистой текущей стоимости не дает ответа на все вопросы, связанные с экономической эффективностью капиталовложений, как отношение результатов проекта к затратам. Этот метод дает ответ лишь на вопрос, способствует ли анализируемый вариант инвестирования росту стоимости фирмы или богатства инвестора, но никак не говорит об относительной мере такого роста. Иными словами метод NPV не позволяет оценить эффект от реализации проекта на единицу затрат.

Одним из факторов, определяющих величину чистой текущей стоимости проекта, является масштаб деятельности, который выражается в физических объемах инвестиций, производства или продаж. Поэтому применение данного метода ограничено для сопоставления различных проектов: большее значение NPV невсегда будет соответствовать более эффективному использованию инвестиций.

В такой ситуации целесообразно рассчитывать показатель рентабельности инвестиций (индекс прибыльности) (PI— profitability index). Формула для определения PI имеет следующий вид:

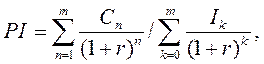
Индекс рентабельности (доходности) инвестиций является относительным показателем, характеризующим уровень доходов на единицу затрат. Чем он выше, тем больше отдача инвестиций в рамках данного проекта. Показатель PI используется в основном при выборе проекта из ряда альтернативных, имеющих близкие значения NPV с разными объемами инвестиций. По этому показателю можно также ранжировать проекты по степени доходности при включении в портфель.

Таким образом, рентабельность инвестиций – это показатель, позволяющий определить, в какой мере возрастает ценность фирмы (богатство инвестора) в расчете на одну денежную единицу инвестиций. Из представленной выше формулы видно, что если рентабельность инвестиций равна единице, то приведенные доходы равны приведенным инвестиционным издержкам и чистый приведенный доход равен нулю. Показатель рентабельности меньше единицы означает неэффективность проекта. Таким образом, эффективные проекты должны иметь показатель рентабельности больший единицы.

Пример. Рассчитать показатель PI для рассмотренного выше примера: первоначальные инвестиции составляют 25 млн. руб., чистая отдача в конце первого года 15 млн. руб., в конце второго года – 10 млн. руб., и третьего года – 8 млн. руб., ставка дисконтирования – 12%.

PI = [15 /(1+0,12)¹ + 10 / (1+0,12)² +8 / (1+0,12)³]/25=27,05/25 = 1,08.

В данном примере приведенный доход составляет 1,08 рубля на каждый рубль инвестиций.

К числу достоинств показателя PI можно отнести:

1. С его помощью можно осуществить ранжирование проектов имеющих примерно одинаковые показатели NPV, т.е. проектов имеющих примерно равные масштабы.

2. Он позволяет оценить степень устойчивости проекта. В рассмотренном выше примере устойчивость невысока, так как снижение чистых денежных поступлений более чем на 8% приведет к тому, что проект станет неэффективным.

Показатель PI в силу алгоритма его расчета тесно связан с показателем NPV. Если величина NPV>0, то PI>1 и проект является эффективным; если NPV<0, то PI<1 и проект следует отвергнуть; если NPV=0, то PI=1 то проект ни прибыльный, ни убыточный. При принятии решения о целесообразности реализации одного инвестиционного проекта можно использовать только один из этих показателей – NPN или PI. При оценке альтернативных проектов следует использовать эти показатели совместно, так как они позволяют инвестору с разных сторон оценить эффективность инвестиций.

При использовании показателя PI для оценки инвестиционных проектов следует помнить, что большее значение индекса доходности не всегда соответствует более высокому значению чистого приведенного дохода, так как PI не учитывает масштабы проекта.

Следующий показатель, входящий в группу сложных методов – внутренняя норма доходности (прибыли) (IRR— internal rate of return). Он рассчитывается путем определения ставки дисконтирования, при которой приведенная стоимость будущих доходов и инвестиционных затрат равны:

На практике внутренняя норма доходности представляет такую ставку дисконтирования, при которой эффект от инвестиций, т.е. чистая настоящая стоимость (NPV), равен нулю. Иначе говоря, приведенная стоимость будущих денежных потоков равна приведенным затратам.

Для рассмотренного выше примера показатель IRR определяется путем решения следующего уравнения

0 = - 25 + 15 /(1+ IRR)¹ + 10 / (1+ IRR)² +8 / (1+ IRR)³.

В рассмотренном нами выше примере IRR=17,3%. При ставке дисконтирования равной 17,3% NPV=0; при больших ставках дисконтирования NPV<0, и, следовательно, проект будет убыточным.

Таким образом, IRR показывает ожидаемую доходность инвестиционного проекта и, соответственно, максимально допустимый относительный уровень расходов в рамках проекта. Иными словами показатель IRR определяет максимальную ставку платы за привлеченные источники финансирования, при котором проект остается безубыточным. При выборе порогового значения внутренней нормы доходности можно ориентироваться на норму дохода по возможным альтернативным инвестициям. Наиболее обоснованным, однако, является выбор в качестве порогового значения IRR средневзвешенной стоимости капитала (WACC), которая отражает сложившийся в коммерческой организации показатель возврата на вложенный капитал.

Таким образом, принятие решения по инвестиционному проекту на основе показателя IRR осуществляется следующим образом. Если внутренняя норма рентабельности инвестиционного проекта (IRR)превышает среднюю стоимость капитала компании, то данный проект может быть рекомендован к реализации, так как он приводит к росту стоимости компании. В противном случае проект следует отвергнуть.

Внутренняя норма прибыли находится обычно методом итерационного подбора значений ставки дисконтирования при вычислении показателя чистой текущей стоимости проекта. Однако этот процесс является трудоемким. Поэтому для расчетов внутренней нормы прибыли используют специальные финансовые калькуляторы. Кроме того, все деловые пакеты программ для персональных калькуляторов содержат встроенную функцию для расчета IRR,

Алгоритм определения IRR методом подбора можно представить в следующем виде. На первом этапе определяется ставка дисконтирования при которой показатель NPV положителен. Далее ставка увеличивается до смены знака показателя NPV и фиксируются ставки r₁, соответствующая последнему положительному значению NPV₁ и r₂, соответствующая первому отрицательному значению NPV₂.(см. табл. 2.8).

Таблица 2.8