Момент импульса и момент силы относительно оси.

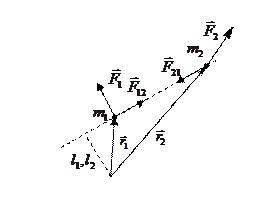
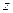Возьмем в интересующей нас системе отсчета произвольную неподвижную ось . Пусть относительно некоторой т.О оси 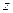момент импульса частицы равен 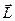, а момент сил 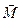. Момент импульса относительно оси 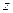называется проекция на эту ось вектора 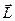, определенного относительно произвольной точки О данной оси. Аналогично вводится понятие момента силы относительно оси 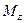. Уравнение момента относительно оси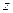 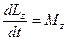т.е. производная от 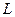относительно 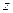равна 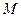относительно этой оси. В частности при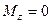 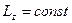. Т.е. если момент илы относительно некоторой оси 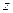равен 0, то 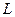относительно этой оси остаеся постоянным. При этом вектор 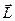меняется.

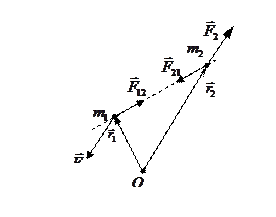4.4. Закон сохранения момента импульса системы.

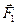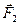Рассмотрим систему состоящую из 2 частиц, на которые действуют также силы и . Момент импульса является аддитивной величиной. Для системы равен векторной сумме моментов импульса отдельных частиц относительно одной и той же точки .

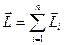Нам известно, что 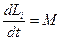—моменту всех сил, действующих на частицу, а изменение момента системы 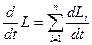, тогда ; ;

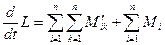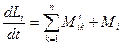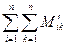— суммарный момент всех внутренних сил действующих на частицы.

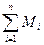— суммарный момент всех внешних сил действующих на частицы.

Значит для двух частиц:

.

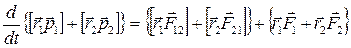Суммарный момент внутренних сил относительно любой точки равен 0. силы взаимодействия между частицами 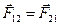по 3^му закону Ньютона действуют по одной прямой, значит имеют одинаковое плечо, поэтому момент каждой пары внутренних сил равен 0.

Т.о. 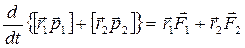; т.е. системы изменяются под действием внешних сил 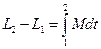. Если внешние силы отсутствуют 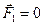, , 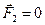то 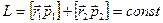, является аддитивным сохраняющейся величиной. Т.е. момент импульса замкнутой системы частиц остается постоянным, не меняется со временем. Это справедливо относительно любой точки инерциальной системы отсчета: 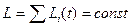т.е. моменты импульса отдельных частей 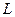одной части системы происходят за счет убыли 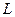другой части (относительно одной точки).

Закон справедлив и в неинерциальной системе отсчета в тех случаях когда суммарный момент всех внешних сил, включая силы инерции равен нулю.

Закон играет такую же роль как закон сохранения энергии импульса. Он позволяет решать разные задачи, не рассматривая детально внутренние процессы. Пример: разгоняют????

Момент импульса 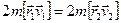; 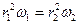т.е. 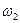уменьшается как 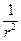. Этот эффект широко используют гимнасты, фигуристы и т.д. здесь мы интересуемся силами взаимодействия и т.д. у незамкнутых систем может сохраняться не сам 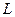, а его проекция на некоторую неподвижную ось 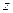. Это бывает, когда 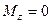всех внешних сил.

; ;

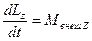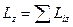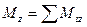
В физике понятие момента импульса расширяют на немеханические системы (с электромагнитным излучением, в атомах, ядра и др.) где не действуют законы Ньютона. Здесь закон сохранения момента импульса уже не является следствием законов Ньютона, а представляет собой самостоятельный принцип, является обобщением опытных фактов и является одним из фундаментальных законов наряду с законами сохранения энергии и импульса.