Решение. Рассматриваемая система имеет одну степень свободы
Рассматриваемая система имеет одну степень свободы. Для определения ускорения 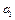 груза 1 выберем в качестве обобщенной координаты его линейное перемещение. Запишем уравнение Лагранжа 2-го рода для выбранной обобщенной координаты х и соответственно для обобщенной скорости
груза 1 выберем в качестве обобщенной координаты его линейное перемещение. Запишем уравнение Лагранжа 2-го рода для выбранной обобщенной координаты х и соответственно для обобщенной скорости 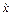
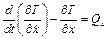 .
.
Механическая система изображена в смещенном положении с учетом положительного направления обобщенной координаты х (см. рис. 3.15). Положительное элементарное приращение обобщенной координаты 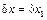 , поэтому величины
, поэтому величины 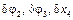 будут элементарными приращениями соответствующих координат. На схеме показаны активные силы тяжести
будут элементарными приращениями соответствующих координат. На схеме показаны активные силы тяжести 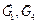 грузов 1, 4 и
грузов 1, 4 и 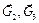 шкивов 2, 3, сила трения
шкивов 2, 3, сила трения 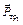 груза 1 о наклонную плоскость, а также моменты
груза 1 о наклонную плоскость, а также моменты 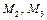 , приложенные к шкивам 2, 3. Вычислим сумму работ всех перечисленных сил и моментов, кроме сил
, приложенные к шкивам 2, 3. Вычислим сумму работ всех перечисленных сил и моментов, кроме сил 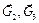 , на элементарных приращениях соответствующих координат с учетом того, что связь между этими приращениями такая же, как и между соответствующими скоростями
, на элементарных приращениях соответствующих координат с учетом того, что связь между этими приращениями такая же, как и между соответствующими скоростями
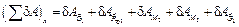 ,
,
где
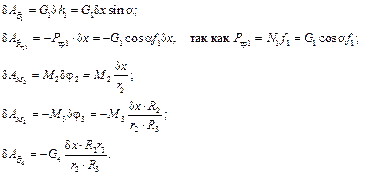
Поскольку 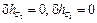 , то работы сил
, то работы сил 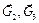 также равны нулю, т.е.
также равны нулю, т.е. 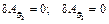 .
.
Подставляя исходные данные, вычислим сумму работ
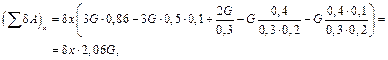
откуда найдем обобщенную силу, соответствующую выбранной обобщенной координате х,
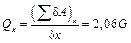 .
.
Кинетическая энергия системы складывается из кинетических энергий тел 1-4, входящих в эту систему,
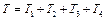 .
.
Для ее нахождения нужно выразить линейные и угловые скорости точек и тел системы через обобщенную скорость 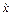 , а затем определить все составляющие:
, а затем определить все составляющие:
– груза 1, совершающего поступательное движение,
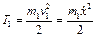 ;
;
– шкива 2, совершающего вращательное движение,
 ,
,
где 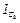 – момент инерции шкива относительно его продольной центральной оси,
– момент инерции шкива относительно его продольной центральной оси, 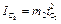 ;
; 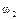 – его угловая скорость,
– его угловая скорость, 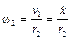 ;
;
– шкива 3, совершающего вращательное движение,
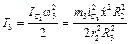 ,
,
где 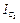 – момент инерции шкива относительно его продольной центральной оси,
– момент инерции шкива относительно его продольной центральной оси, 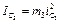 ;
;  – его угловая скорость,
– его угловая скорость, 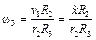 ;
;
– груза 4, совершающего поступательное движение,
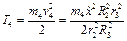 ,
,
где 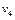 – скорость груза,
– скорость груза, 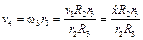 .
.
Теперь подставим все полученные выражения для кинетических энергий тел 1-4 и исходные данные в формулу для полной кинетической энергии системы
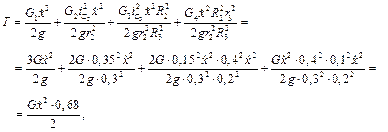
откуда найдем
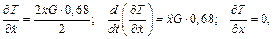
так как обобщенная координата х в формулу для кинетической энергии не входит.
Подставляя полученные значения в уравнение Лагранжа 2-го рода
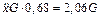 ,
,
далее определим линейное ускорение груза 1
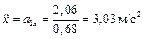 .
.
Найдем силу натяжения троса, равную по величине реакции 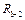 , мысленно разрезав его и изобразив все силы, действующие на груз 1, считая груз материальной точкой (рис. 3.16).
, мысленно разрезав его и изобразив все силы, действующие на груз 1, считая груз материальной точкой (рис. 3.16).
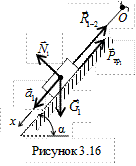 Запишем основное уравнение динамики материальной точки в векторной форме
Запишем основное уравнение динамики материальной точки в векторной форме
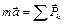 ,
,
и в проекции на ось Ох
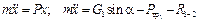 .
.
С учетом того, что 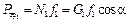 , получим
, получим
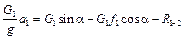 ,
,
откуда, подставляя исходные данные, найдем
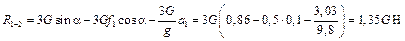 .
.
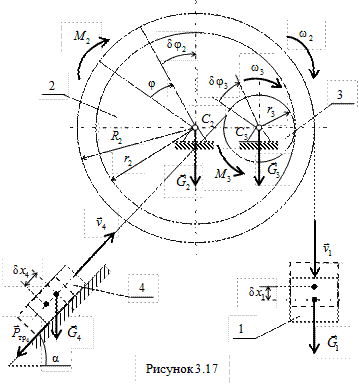
Пример 11. Механическая система состоит из грузов 1, 4 и барабанов 2, 3, связанных между собой (рис. 3.17). К барабану 2 весом 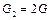 Н, радиусами
Н, радиусами 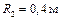 ,
, 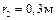 и радиусом инерции
и радиусом инерции 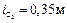 приложена пара сил, момент которой
приложена пара сил, момент которой 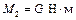 . Этот момент приводит систему в движение. К барабану 3 весом
. Этот момент приводит систему в движение. К барабану 3 весом 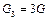 Н радиусом
Н радиусом 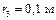 приложена пара сил сопротивления, момент которой
приложена пара сил сопротивления, момент которой 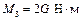 . Груз 1 весом
. Груз 1 весом 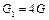 Н опускается вертикально вниз. Груз 4 весом
Н опускается вертикально вниз. Груз 4 весом 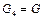 Н поднимается по шероховатой наклонной плоскости, расположенной под углом
Н поднимается по шероховатой наклонной плоскости, расположенной под углом 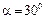 к горизонту. Коэффициент трения груза 4 о наклонную плоскость
к горизонту. Коэффициент трения груза 4 о наклонную плоскость 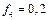 . Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, нерастяжимыми и невесомыми. Барабан 3 – сплошной однородный цилиндр.
. Все тела, входящие в систему, являются абсолютно твердыми, а тросы (идеальные нити), которыми они соединены между собой, нерастяжимыми и невесомыми. Барабан 3 – сплошной однородный цилиндр.
Определить угловое ускорение барабана 2 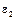 и силу натяжения троса, соединяющего тела 1-2 в зависимости от параметра
и силу натяжения троса, соединяющего тела 1-2 в зависимости от параметра 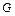 .
.
Дата добавления: 2015-06-17; просмотров: 1164;
