Решение. Приложим к рассматриваемой механической системе, состоящей из вала и стержней с грузами, все внешние силы
Приложим к рассматриваемой механической системе, состоящей из вала и стержней с грузами, все внешние силы 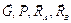 , действующие на эту систему. Ось Аz совпадает с осью вращения вала. Запишем выражение для теоремы об изменении кинетического момента системы в векторной форме и в проекциях на ось Аz:
, действующие на эту систему. Ось Аz совпадает с осью вращения вала. Запишем выражение для теоремы об изменении кинетического момента системы в векторной форме и в проекциях на ось Аz:
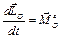 ;
;
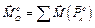 ;
;
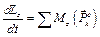 .
.
Так как линии действия сил тяжести 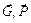 параллельны оси Аz, а реакции подпятника
параллельны оси Аz, а реакции подпятника 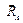 и подшипника
и подшипника 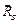 пересекают ее, то
пересекают ее, то 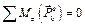 и, следовательно, имеет место закон сохранения кинетического момента системы относительно оси Аz, т.е.
и, следовательно, имеет место закон сохранения кинетического момента системы относительно оси Аz, т.е. 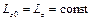 .
.
Кинетический момент системы при горизонтальном расположении стержней определим суммой
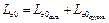 .
.
Абсолютная скорость каждого из грузов
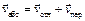 .
.
Так как линия действия вектора 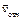 пересекает ось Аz, то составляющие кинетического момента относительно оси вращения от относительного движения грузов равны нулю, поэтому
пересекает ось Аz, то составляющие кинетического момента относительно оси вращения от относительного движения грузов равны нулю, поэтому
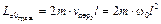 ;
; 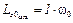 .
.
Кинетический момент системы при отклонении стержней на угол α определим суммой
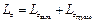 ,
,
где
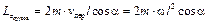 ;
; 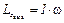 .
.
Приравнивая выражения для проекций кинетических моментов 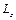 и
и 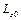 , окончательно получим
, окончательно получим
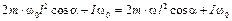 ,
,
откуда найдем угловую скорость вала
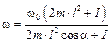 .
.
Дата добавления: 2015-06-17; просмотров: 787;
