Решение. Механическая система, состоящая из барабана и двух грузов, показана в текущем положении (см
Механическая система, состоящая из барабана и двух грузов, показана в текущем положении (см. рис. 3.8) со всеми внешними силовыми факторами 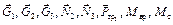 , действующими на нее. Ось координат Oz совпадает с осью вращения барабана. Запишем выражения для теоремы об изменении кинетического момента системы в векторной форме и в проекции на эту ось:
, действующими на нее. Ось координат Oz совпадает с осью вращения барабана. Запишем выражения для теоремы об изменении кинетического момента системы в векторной форме и в проекции на эту ось:
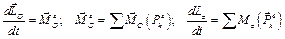 .
.
Теперь вычислим проекцию кинетического момента системы на ось Oz по формуле
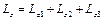 ,
,
где
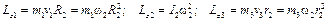 ,
,
откуда найдем
 .
.
Далее определим алгебраическую сумму моментов всех внешних сил, действующих на систему, относительно оси Oz
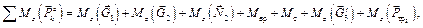
где
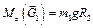 ;
;
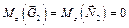 ;
;
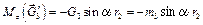 ,
,
так как силу 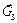 разложили на две составляющие
разложили на две составляющие 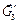 и
и 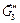 ;
;
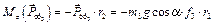 .
.
В данном случае сила трения перенесена в точку приложения силы тяжести, а компенсирующая этот перенос пара сил уравновешена реакциями опор груза 3. Подставляя в алгебраическую сумму в полученные выражения, определим
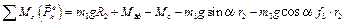 .
.
Теперь найдем первую производную от проекции кинетического момента на ось Oz:
 .
.
Подставляя полученные результаты в выражение для теоремы об изменении кинетического момента системы, окончательно запишем
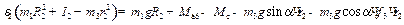 .
.
Из этого уравнения определим угловое ускорение барабана 2 и ускорения грузов 1, 3
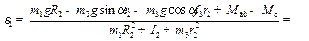
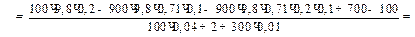
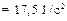 ;
;
 ;
;
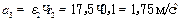 .
.
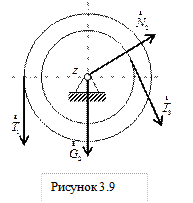
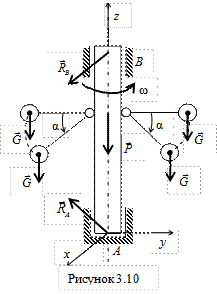
Найдем реакции двух ветвей троса (см. рис. 3.8 и 3.9)
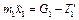 ;
;
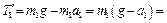
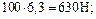
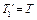 ;
;
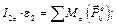
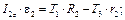
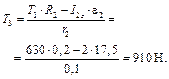
 Пример 7. Два невесомых стержня с точечными грузами на концах массой m и длиной l каждый закреплены шарнирами на вертикальном валу (рис. 3.10). Вал при горизонтальном расположении стержней вращается с угловой скоростью
Пример 7. Два невесомых стержня с точечными грузами на концах массой m и длиной l каждый закреплены шарнирами на вертикальном валу (рис. 3.10). Вал при горизонтальном расположении стержней вращается с угловой скоростью 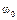 , его момент инерции относительно оси вращения І. В некоторый момент времени стержни начинают отклоняться от горизонтального положения, составляя с горизонталью угол α.
, его момент инерции относительно оси вращения І. В некоторый момент времени стержни начинают отклоняться от горизонтального положения, составляя с горизонталью угол α.
Определить угловую скорость вала в зависимости от угла α. Сопротивление воздушной среды, подшипника и подпятника, в которых установлен вал, не учитывать.
Дата добавления: 2015-06-17; просмотров: 1194;
