Максимальная и минимальная работы процесса. Термодинамические потенциалы

По изменению характеристических функций можно определить максимальную работу немеханического характера при соответствующих условиях сопряжения ТС с окружающей средой, т.е. при двух фиксированных независимых параметрах. Так, для сложной закрытой ТС, в которой протекают процессы с двумя фиксированными параметрами, находящимися под знаками дифференцирования в правых частях объединенных выражений 1-го и 2-го законов термодинамики (1)-(4) получим следующие соотношения:

при S, V=const 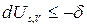ℒ_s,V , (22)

при S, p=const ℒ_s,p , (23)

при T, V=const ℒ_T,V, (24)

при T, p=const 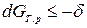ℒ_T,p, (25)

где 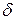ℒ= 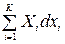- сумма работ немеханического характера. Для конечного процесса 1-2 эти выражения запишем в виде, умножив левые и правые части уравнений (22)-(25) на минус единицу (-1). Тогда:

ℒ_s,V, (26)

ℒ_s,p, (27)

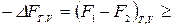ℒ_T,V, (28)

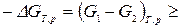ℒ_T,p, (29)

При протекании обратимых процессов работа немеханического характера ℒ максимальна и равна уменьшению соответствующей характеристической функции, т.е.:

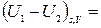ℒ_{s,V max},

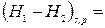ℒ_{s,p max},

(30)

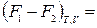ℒ_{T,V max},

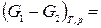ℒ_{T,p max}.

При протекании необратимых процессов с максимальными потерями работоспособности ТС работа немеханического характера равна нулю, т.е.

ℒ_min=0. (31)

В общем случае при необратимых процессах часть энергии упорядоченного движения материи диссипирует (рассеивается) в энергию теплового неупорядоченного движения и работа немеханического характера ТС ℒ будет меньше максимальной работы в обратимых процессах.

В термодинамике характеристические функции: U, H, F, G, дифференциалы которых с обратным знаком равны элементарной работе немеханического характера, называют термодинамическими потенциалами:

U – изохорно-изоэнтропийный потенциал,

H – изобарно-изоэнтропийный потенциал,

F – изохорно-изотермический потенциал,

G – изобарно-изотермический потенциал.

Уменьшение термодинамических потенциалов при фиксации двух параметров в обратимых процессах равно максимальной работе ТС.

Таким образом, сумма работ немеханического характера может быть определена через изменения характеристических функций при фиксации двух независимых параметров.