Расчетные выражения для скорости звука в общем виде
По определению адиабатная скорость звука равна:
 , (1)
, (1)
где плотность газа  и
и 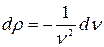 . Тогда:
. Тогда:
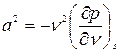 . (2)
. (2)
По уравнению связи частных производных одного параметра по другому имеем:
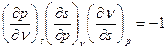 , откуда:
, откуда:
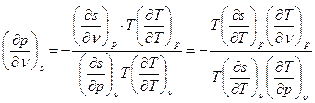 .
.
По определению изобарная и изохорная удельные теплоемкости равны:
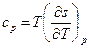 и
и  . Тогда
. Тогда
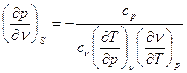 . (3)
. (3)
После подстановки выражения (3) в (2) имеем:
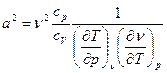 . (4)
. (4)
По уравнению связи:
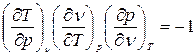 , имеем:
, имеем:
 . (5)
. (5)
После подстановки выражения (5) в (4) окончательно имеем выражение для расчета скорости звука в общем виде:
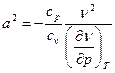 . (6)
. (6)
Из формулы (6) получим формулу для расчета скорости звука в идеальном газе при условии, что удельная газовая постоянная R не зависит от давления и температуры. Тогда из уравнения состояния для 1 кг идеального газа: 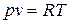 , имеем
, имеем 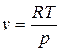 и производную
и производную 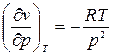 . После подстановки выражения для
. После подстановки выражения для 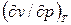 в формулу (6) получим:
в формулу (6) получим:
 , где
, где  - показатель адиабаты,
- показатель адиабаты, 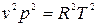 . Тогда:
. Тогда:  - скорость звука в идеальном газе.
- скорость звука в идеальном газе.
Дата добавления: 2015-06-12; просмотров: 889;
