Различные формы записи объединенных выражений
Для сложных открытых ТС уравнения первого закона термодинамики, выраженные через изменения внутренней энергии и энтальпии имеют вид:
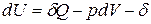 ℒ
ℒ 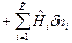 ,
,
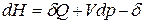 ℒ
ℒ 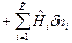 .
.
Математическое выражение 2-го закона термодинамики:
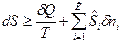 ,
,
представим в виде: 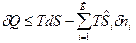 , и подставим в уравнение 1-го закона термодинамики.
, и подставим в уравнение 1-го закона термодинамики.
Тогда получим объединенные выражения для изменения внутренней энергии dU и энтальпии dH:
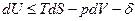 ℒ
ℒ 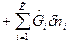 , (1)
, (1)
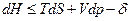 ℒ
ℒ 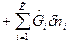 (2)
(2)
где 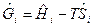 - молярная свободная энергия Гиббса, Дж/моль.
- молярная свободная энергия Гиббса, Дж/моль.
G=H-TS, Дж, - свободная энергия Гиббса, которая является функцией состояния. Функцией состояния является также свободная энергия Гельмгольца:
F=U-TS Дж.
Дифференциалы dF и dG – полные дифференциалы:
dF=dU-TdS-SdT,
dG=dH-TdS-SdT.
Вместо dU и dH подставим в эти выражения их значения по уравнениям (1) и (2). Тогда получим еще две формы записи объединенных выражений 1-го и 2-го законов термодинамики для функций F и G:
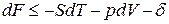 ℒ
ℒ 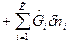 , (3)
, (3)
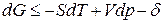 ℒ
ℒ 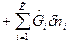 (4)
(4)
Функции состояния ТС: внутренняя энергия U, энтальпия Н и свободные энергии Гельмгольца F и Гиббса G называются характеристическими функциями при определенном выборе независимых переменных.
Дата добавления: 2015-06-12; просмотров: 850;
