Термические и калорические уравнения состояния

Общее число термических и калорических уравнений состояния ТС определяется числом ее степеней свободы, т.е. числом воздействующих на ТС обобщенных сил. Эти уравнения устанавливаются опытным путем или находится методами статистической физики.

Для простой ТС (число степеней свободы N=2), на которую действует одна обобщенная сила механического характера – давление р, сопряженная внешнему параметру V, взаимодействие с окружающей средой характеризуется только одним внешним параметром, изменяющимся при данном взаимодействии, (обобщенной координатой) – объемом V и температурой Т (независимый параметр). Тогда равновесные внутренние параметры состояния: давление и внутреннюю энергию U можно выразить в виде функциональных зависимостей: p=p(V,T) – термического уравнения состояния и U=U(V,T) – калорического уравнения состояния.

Термическое уравнение состояния для простой ТС можно представить в виде связи: F(p,V,T)=0. Это уравнение является уравнением термодинамической поверхности или поверхности состояний. Для идеального газа термическим уравнением состояния является уравнение Клапейрона: pV=mRT, где R – удельная газовая постоянная.

Калорическое уравнение состояния идеального газа можно получить из закона Джоуля: «Внутренняя энергия термодинамической системы U при Т=const не зависит от объема V:

.

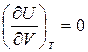Продифференцировав уравнение U=U(V,T), получим:

,

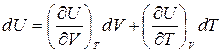где 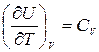- теплоемкость идеального газа в процессе V=const (по определению).

Тогда

,

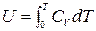т.е. внутренняя энергия идеального газа является функцией только температуры:

.

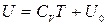Калорическое и термическое уравнения состояния идеального газа можно также получить из молекулярно-кинетических представлений.