Термические уравнения состояния для реальных газов

Конкретный вид термического уравнения зависит от агрегатного состояния и рода вещества. В настоящее время хорошо разработаны уравнения состояния только для реальных газов. Для конденсированных веществ уравнения состояния встречаются крайне редко, поскольку для практических расчетов они и не требуются.

Вид уравнения состояния для реальных газов сильно зависит от размера частиц, их структуры и характера взаимодействия между ними. Потенциальная энергия взаимодействия U двух молекул зависит от расстояния между их центрами – r , т.е. U=f(r). Молекулы реальных газов имеют конечные размеры и притягиваются друг к другу с силами, которые возрастают с уменьшением среднего расстояния между молекулами, в отличие от идеального газа, у которого U(r)=0.

Для расчетов потенциальной энергии U в большинстве случаев используется потенциал Леннарда-Джонса:

.

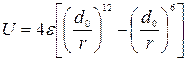Обозначения величин 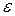и d₀ приведены на рисунке, изображающем данную зависимость U=f(r).

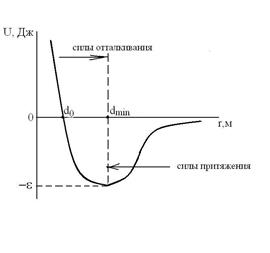
Силы взаимодействия между молекулами 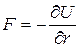, [Н], очень велики при малых расстояниях между молекулами (силы отталкивания) и не позволяют уменьшить объем газа ниже определенного предела (ниже расстояния r=d_min). Этот потенциал относится к группе вандерваальсовских (дальнедействующих) сил. Для больших расстояний r потенциал U~1/r⁶, а сила взаимодействия F~1/r⁷. Для малых расстояний r (при сильном сближении молекул) U~1/r¹², а F~1/r¹³.

Для сравнения отметим, что для кулоновских взаимодействий потенциал U~1/r, а сила F~1/r². Таким образом, вандерваальсовские силы убывают с ростом расстояния r между частицами гораздо быстрее, чем кулоновские силы. Поэтому уравнение состояния для реальных газов обычно не пригодны для плазмы. Для плазмы уравнение состояния выводится отдельно (Дебай).

Зависимости сил взаимодействия от расстояния между частицами (F=f(r)) используются для вычисления коэффициентов, входящих в различные уравнения состояния реальных газов и плазмы.

Наиболее простым уравнением состояния для реальных газов является уравнение Ван-дер-Ваальса (1873г.) (в настоящее время имеется более 150 эмпирических уравнений). Это уравнение имеет вид:

,

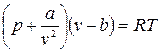где b – поправка на объем молекул, a/v² – поправка на внутреннее или молекулярное давление, определяемое взаимным притяжением молекул газа. Константы a и b зависят от рода газа (от природы вещества).

Для жидкостей это уравнение сильно расходится с данными опыта. Это уравнение указывает на возможность существования двух фаз и приводит к выводу о существовании критической точки. Если отнести параметры p, T, v к критическим параметрам p_к, Т_к,v_к в критической точке фазовой диаграммы и обозначить 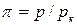, , 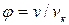, 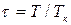то получим приведенное уравнение Ван-дер-Ваальса:

,

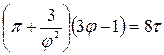которое выражает закон соответственных состояний.

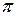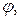
Соответственными состояниями называются состояния различных веществ, имеющих одинаковые приведенные параметры , 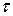. Вещества одинаковой химической природы, удовлетворяющие этому уравнению являются термодинамически подобными, если их критические коэффициенты одинаковы:

.

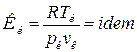Для вадерваальсовского газа К_к=2,67.

Отклонение свойств реальных газов от свойств идеального газа можно охарактеризовать величиной сжимаемости или коэффициента сжимаемости

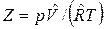или .

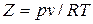Для идеального газа Z=1. Для реального газа Z≠1. Величина коэффициента сжимаемости зависит от давления, температуры и рода газа и может быть как больше, так и меньше единицы в зависимости от этих факторов.

Уравнения состояния могут быть получены для реального газа, рассматривая взаимодействие частиц. Эти уравнения называются вириальными уравнениями состояния, которые в V – форме имеют вид:

,

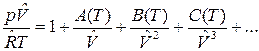где А(Т), В(Т), С(Т) – первый, второй и третий вириальные коэффициенты, зависящие от температуры. В р-форме вириальное уравнение имеет вид:

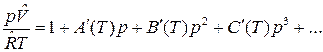
Коэффициенты А(Т), В(Т), С(Т) связаны с коэффициентами А´(Т), В´(Т), С´(Т).

Первый коэффициент А(Т) определяется парными столкновениями частиц, второй коэффициент В(Т) – тройными столкновениями частиц и т.д. Одновременное столкновение большого числа частиц – маловероятно. Наибольшую роль играют парные столкновения частиц. При их учете в правой части вириального уравнения сохраняются только два слагаемых. Примером такого уравнения является уравнение Ван-дер-Ваальса. Коэффициент А(Т) определяется путем интегрирования потенциала парного столкновения. Чем выше давление, тем большее число слагаемых в правой части вириального уравнения следует учитывать.

Термические уравнения состояния для различных веществ устанавливаются также по опытным данным для сжимаемости Z=p 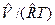, для теплоемкости С=f(p,T) и для температурного эффекта дросселирования. Надо иметь в виду, что использование уравнения состояния для идеальных газов дает приближенные результаты, справедливые для реальных газов, обладающих малой плотностью, т.е. при небольших давлениях и больших температурах.