Дифракционная решетка. Рассмотрение дифракции на двух щелях показывает, что в этом случае дифракционные максимумы становятся более узкими

Рассмотрение дифракции на двух щелях показывает, что в этом случае дифракционные максимумы становятся более узкими, чем в случае одной щели. Увеличение числа щелей делает это явление еще более отчетливым.

Повторяя рассуждение §6, найдем, что между каждыми двумя главными максимумами (dsinφ=0, λ , 2λ , 3λ, ...) при трех щелях располагаются два добавочных минимума (dsinφ = 1/3 λ и 2/3 λ , 4/3 λ и 6/3 λ и т. д.), при четырех щелях — три добавочных минимума и т. д.

В общем случае N щелей ширины b с промежутками а (период решетки d = а + b) имеем:

прежние минимумы b sinφ= λ , 2λ , 3λ , …

главные максимумы d sinφ= 0 λ , 2 λ , 3 λ , …

добавочные минимумы d sinφ= λ/N , 2λ/N , …, (N-1)λ/N, (N+1) λ/N , …

т. е. между двумя главными максимумами располагается (N — 1) добавочных минимумов, разделенных вторичными максимумами. Конечно, с увеличением числа щелей растет интенсивность главных максимумов, ибо возрастает количество пропускаемого решеткой света. Однако самое существенное изменение, вносимое большим числом щелей, состоит в превращении расплывчатых максимумов в резкие узкие максимумы, разделенные практически темными промежутками, ибо вторичные максимумы очень слабы: самый сильный из наблюденных вторичных максимумов составляет не более 5% от главного. Резкость максимумов обеспечивает возможность надежно отличать близкие длины волн, для которых главные максимумы не будут перекрывать друг друга, что имеет место при расплывчатых максимумах, получающихся с одной щелью или малым числом их.

То обстоятельство, что в результате интерференции большого числа лучей мы получаем резкий переход (малое изменение направления φ ) от максимума к соседнему минимуму, наглядно объясняется диаграммами рис. 5.1. Когда все складывающиеся N лучей находятся в одной фазе, мы получаем максимум, соответствующий амплитуде s = Na, результирующего колебания, где N — число интерферирующих лучей и а — амплитуда каждого из них. Для получения минимума (см. рис. 5.1, в) необходимо, чтобы фаза последнего луча отличалась от фазы первого на 2π . Следовательно, при наличии N лучей различие в фазе двух соседних лучей должно равняться 2π/N (различие в разности хода λ/N) т, е. быть тем меньше, чем больше N.

Таким образом, между каждыми двумя главными максимумами, соответствующими разности хода dsinφ=тλ , где т = 0, ±1, ±2, ..., лежат по (N — 1) добавочных минимумов, определяемых разностью хода dsinφ=тλ+рλ/N где р пробегает целые значения от 1 до (N - 1). Угловое расстояние между главным максимумом и соседним минимумом определяется требованием, чтобы разность хода возросла на λ/N, т. е. Δ(dsinφ) = λ/N, или dcosφ Δφ = тλ+рλ/N , откуда Δφ = λ/Nd cosφ . При не очень больших углах дифракции (cosφ~1 ), что соответствует обычно не очень большим порядкам дифракции (небольшим т), резкость главных максимумов не зависит от порядка спектра и равна Δφ = λ/Nd. Из этой формулы следует, что резкость главных максимумов тем больше, чем больше Nd, т. е. чем больше общая ширина решетки. При заданном периоде решетки d, резкость главных максимумов возрастает (Δφ уменьшается) с ростом числа штрихов N.

Расстояние между главными максимумами для определенной длины волны λ определяется периодом решетки d, а распределение интенсивности между отдельными максимумами зависит от соотношения между b и d. В том случае, когда b и d соизмеримы, некоторые главные максимумы будут отсутствовать. Так, при d = 2b пропадают все четные максимумы, причем, конечно, соответствующим образом усиливаются нечетные. При d = 3b исчезает каждый третий максимум и т. д.

Общая формула, передающая распределение амплитуд дифраги­ровавших волн в зависимости от угла φ, гласит:

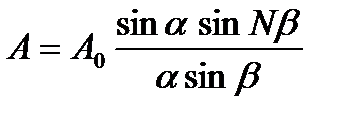(7.1)

где α=(πb/λ) sinφ, β==(πd/λ) sinφ, N — число щелей и A₀ — амплитуда, задаваемая одной щелью в направлении первичного пучка φ = 0. Формула (7.1) получается без труда, если суммировать действия отдельных щелей, принимай во внимание возникающую разность фаз. Множитель 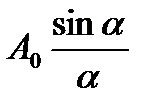выражает действие одной щели, а множитель 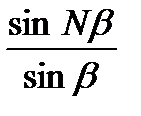— интерференцию волн, распространяющихся через N щелей. Положение главных максимумов, определяемое из условия dsinφ=тλ, соответствует максимальным значениям множителя 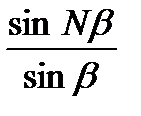, который при этом

обращается в N.

Таким образом, в главных максимумах амплитуда в N раз, а интенсивность в N² раз больше, чем дает в соответствующем направлении одна щель. Если бы интерферировали волны, прошедшие через N некогерентно освещенных щелей, то интенсивность возросла бы только в N раз, т. е. была бы в N раз меньше, чем при интерференции когерентных пучков, обусловленных решеткой. Кроме того, в случае решетки отдельные яркие главные максимумы разделены темными областями, а при N некогеректно освещенных щелях мы имели бы N-кратное наложение сравнительно широкой дифракционной картины от одной щели. Формула (7.1) показывает, что в выражение для распределения амплитуды входит множитель 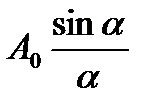, дающий распределение, обусловленное одной щелью. Следовательно, при дифракции на решетке, так же как и при дифракции от двух щелей, почти весь свет сосредоточен в области центрального максимума, обусловленного одной щелью. Так как ширина щели b обычно очень мала, то этот центральный максимум с угловой шириной, равной 2λ/b, довольно широк, и на его протяжении укладывается несколько главных максимумов решетки, соответствующих нескольким порядкам.

Рассмотрение действия дифракционной решетки показывает, что при большом числе щелей свет, прошедший через решетку, собирается в отдельных, резко очерченных участках экрана. Положение максимумов на этих участках, определяемое формулой dsinφ=тλ, зависит от длины волны λ. Другими словами, дифракционная решетка представляет собой спектральный прибор.

Чем меньше длина волны λ, тем меньшему значению угла φ соответствует положение максимума. Таким образом, белый свет растягивается в спектр так, что внутренний край его окрашен в фиолетовый цвет, а наружный — в красный. Значение т = 0 определяет максимум по направлению φ=0 для всех значений λ. Следовательно, в этом направлении (направление первичного пучка) собирается излучение всех длин волн, т. е. нулевой спектр представляет собой белое изображение источника.

Спектры первого, второго и т. д. порядков располагаются симметрично по обе стороны нулевого. Расстояние между соответствующими линиями спектров возрастает по мере увеличения порядка спектров. В зависимости от спектральной однородности анализируемого света, т. е. различия крайних длин волн, его составляющих, спектры высших порядков начинают накладываться друг на друга. Так, для солнечного света, даже если ограничиться лишь видимой частью его излучения, спектры второго и третьего порядков частично перекрывают друг друга. Применяя решетки с малым периодом и пользуясь спектрами высших порядков, мы можем получить значительные углы дифракции и таким образом очень точно измерить длины волн. Измерения Ангстрема (1868 г.) и, особенно, Роулэнда (1888 г.) привели к составлению превосходных атласов солнечного спектра, положения фраунгоферовых линий которого измерены с точностью до шестого десятичного знака.

Несмотря на высокое совершенство изготовления современных решеток, в них нередко наблюдаются некоторые незначительные искажения единого строго выраженного на всем протяжении решетки периода, существование которого мы предполагали при нашем рассмотрении. Это влечет за собой отступление от расчетного распределения интенсивности по главным максимумам.

Сверх того, указанные нарушения влекут за собой появление добавочных максимумов, обычно не сильных (так называемых «духов»). Появление «духов» нередко приводит к ошибкам при анализе спектра дифракционной решеткой, ибо максимум, соответствующий «духу», можно принять за присутствие какой-то добавочной спектральной липни, в анализируемом спектре в действительности не имеющейся.