Дифракционная решётка
Дифракциейназывается любое отклонение распространения света от прямолинейного, не связанное с отражением и преломлением. Качественный метод расчета дифракционной картины предложил Френель. Основной идеей метода является принцип Гюйгенса - Френеля:
Каждая точка, до которой доходит волна, служит источником когерентных вторичных волн, а дальнейшее распространение волны определяется интерференцией вторичных волн.
Геометрическое место точек, для которых колебания имеют одинаковые фазы, называют волновой поверхностью. Волновой фронт также является волновой поверхностью.
Дифракционная решеткапредставляет собой совокупность большого числа параллельных щелей или зеркал одинаковой ширины и отстоящих друг от друга на одинаковом расстоянии.Периодом решетки (d)называется расстояние между серединами соседних щелей, или что то же самое сумма ширины щели (а) и непрозрачного промежутка (b)между ними (d = a + b).
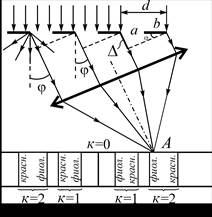
Рассмотрим принцип действия дифракционной решетки. Пусть на решетку нормально к её поверхности падает параллельный пучок лучей белого света (рис. 1). На щелях решетки, ширина которых соизмерима с длиной волны света, происходит дифракция.
|
| Рис. 1. Ход лучей в дифракционной решетке |
В результате за дифракционной решеткой согласно принципу Гюйгенса-Френеля от каждой точки щели световые лучи будут распространяться во всех возможных направлениях, которым можно сопоставить углы отклонения φ световых лучей (углы дифракции) от первоначального направления. Параллельные между собой лучи (дифрагирующие под одинаковым углом φ) можно сфокусировать, установив за решеткой собирающую линзу. Каждый пучок параллельных лучей соберется в задней фокальной плоскости линзы в определённой точке А. Параллельные лучи, соответствующие другим углам дифракции, соберутся в других точках фокальной плоскости линзы. В этих точках будет наблюдаться интерференция световых волн, исходящих от разных щелей решетки. Если оптическая разность хода между соответствующими лучами монохроматического света будет равна целому числу длин волн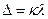 
, κ = 0, ±1, ±2, …, то в точке наложения лучей будет наблюдаться максимум интенсивности света для данной длины волны, Из рисунка 1 видно, что оптическая разность хода Δ между двумя параллельными лучами, выходящими из соответствующих точек соседних щелей, равна
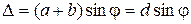, (1)
где φ – угол отклонения луча решеткой.
Следовательно, условие возникновения главных интерференционных максимумов решетки или уравнение дифракционной решетки
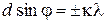, (2)
где λ – длина световой волны.
В фокальной плоскости линзы для лучей, не испытавших дифракции, наблюдается центральный белый максимум нулевого порядка (φ = 0, κ = 0), справа и слева от которого располагаются цветные максимумы (спектральные линии) первого, второго и последующих порядков (рис. 1). Интенсивность максимумов уменьшается с ростом их порядка, т.е. с увеличением угла дифракции.
Уравнение (1) позволяет рассчитать длину волны падающего света, если измерен угол дифракции φ, для данной спектральной линии, известны период дифракционной решетки d и порядок спектра k.
Зная период решетки, можно рассчитать число штрихов n, нанесенных на 1 мм ширины решетки:
. (3)
Одной из основных характеристик дифракционной решетки является её угловая дисперсия. Угловая дисперсия решетки определяет угловое расстояние dφ между направлениями для двух спектральных линий, отличающихся по длине волны на 1 нм (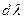 
= 1 нм), и характеризует степень растянутости спектра вблизи данной длины волны:
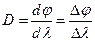. (4)
Формула для расчета угловой дисперсии решетки может быть получена при дифференцировании уравнения (2)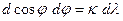 
. Тогда
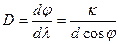. (5)
Из формулы (5) следует, что угловая дисперсия решетки тем больше, чем больше порядок спектра.
Для решеток с разными периодами ширина спектра больше у решетки, характеризующейся меньшим периодом. Обычно в пределах одного порядка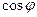 
меняется незначительно (особенно для решеток с небольшим числом штрихов на миллиметр), поэтому дисперсия в пределах одного порядка почти не меняется. Спектр, полученный при постоянной дисперсии, растянут равномерно во всей области длин волн, что выгодно отличает спектр решетки от спектра, даваемого призмой.
Угловая дисперсия связана с линейной дисперсией 
. Линейную дисперсию можно также вычислить по формуле
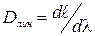, (6) где 
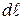– линейное расстояние на экране или фотопластинке между спектральными линиями, f – фокусное расстояние линзы.
Дифракционная решетка также характеризуется разрешающей способностью. Этавеличина, характеризующая способность дифракционной решетки давать раздельное изображение двух близких спектральных линий
R =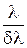 
, (7)
где l – средняя длина волны разрешаемых спектральных линий; dl – разность длин волн двух соседних спектральных линий.
Зависимость разрешающей способности от числа щелей дифракционной решетки N определяется формулой
R = 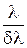= kN, (8)
где k – порядок спектра.
Из уравнения для дифракционной решетки (1) можно сделать следующие выводы:
1. Дифракционная решетка будет давать заметную дифракцию (значительные углы дифракции) только в том случае, когда период решетки соизмерим с длиной световой волны, то есть d »l» 10 –4 см. Решетки с периодом меньше длины волны не дают дифракционных максимумов.
2. Положение главных максимумов дифракционной картины зависит от длины волны. Спектральные составляющие излучения немонохроматического пучка отклоняются решеткой на разные углы (дифракционный спектр). Это позволяет использовать дифракционную решетку в качестве спектрального прибора.
3. Максимальный порядок спектра, при нормальном падении света на дифракционную решетку, определяется соотношением:
kmax £ d ¤l.
Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем и частотой штрихов, что позволяет перекрыть область спектра от ультрафиолетовой его части (l » 100 нм) до инфракрасной (l » 1 мкм). Широко используются в спектральных приборах гравированные решетки (реплики), которые представляют собой отпечатки решеток на специальных пластмассах с последующим нанесением металлического отражательного слоя.
Дата добавления: 2015-06-10; просмотров: 12333;