Дифракционная решетка

Дифракционная решётка – оптическое устройство, представляющее собой совокупность большого числа регулярно расположенных штрихов (щелей, канавок, выступов), нанесенных тем или иным способом на плоскую или вогнутую оптическую поверхность, на которых происходит дифракция света. Обычно дифракционная решётка представляет собой совокупность большого числа параллельных штрихов одинаковой ширины, нанесенных на прозрачную или отражающую поверхность на одинаковом расстоянии друг от друга. В дифракционной решетке наблюдается многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Фронт световой волны, падающий на дифракционную решётку, разбивается её штрихами на отдельные когерентные пучки, которые, претерпев дифракцию на штрихах, интерферируют, образуя результирующее пространственное распределение интенсивности света – спектр излучения. Существуют отражательные и прозрачные дифракционные решётки.

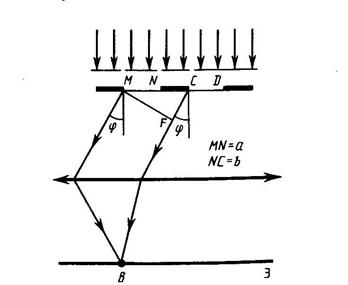Расстояние между серединами соседних щелей 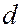называется постоянной или периодом решетки. Рассмотрим случай нормального падения монохроматического света с длиной волны 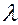на прозрачную одномерную дифракционную решётку с периодом 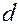, состоящую из 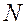одинаковых параллельных щелей шириной 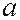. Расположим параллельно решетке собирающую линзу, в фокальной плоскости которой расположим экран. Каждая из щелей дает на экране картину, описываемую формулами (6.37.28) и (6.37.29).

Для направлений, удовлетворяющих условию

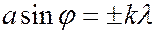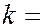( 1, 2, 3, ….), (6.37.32)

амплитуды колебаний, приходящие от всех щелей в точку 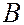, равны нулю, поэтому и амплитуда результирующего колебания в соответствующей точке экрана равна нулю. Условие минимумума для одной щели (6.37.28) является

условием минимума для дифракционной решетки (6.37.32).

Для направлений, удовлетворяющих условию

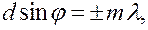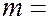( 0, 1, 2, …) (6.37.33)

разность хода лучей от сходственных точек соседних щелей равна целому числу длин волн. Колебания от всех щелей в точку, удовлетворяющую условию (6.37.33) приходят в одной фазе и усиливают друг друга. Формула (6.37.33) определяет положение главных максимумов дифракционной решетки.

Вследствие взаимной интерференции световых лучей посылаемых щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Для направлений, удовлетворяющих условию

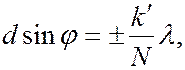
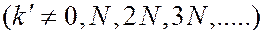(6.37.34)

колебания от отдельных щелей взаимно погашают друг друга. В этих направлениях результирующая амплитуда будет равна нулю. Формула (6.37.34) определяет положение дополнительных (вторичных) минимумов. Между дополнительными минимумами располагаются слабые вторичные максимумы. Результирующая дифракционная картина, получающаяся от решетки имеет вид:

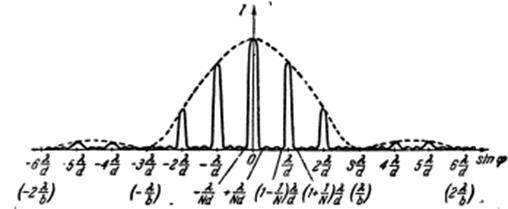
Количество наблюдающихся главных максимумов зависит от отношения периода решетки к ширине щели:

(6.37.35)

При выполнении условия 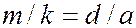(период решетки и ширина щели относятся как целые числа) 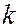-й минимум совпадает с максимумом 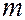-го порядка, в этом случае 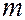-й максимум пропадает.

Угловая ширина центрального максимума

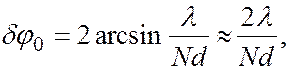(6.37.36)

угловая ширина 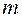-го максимума

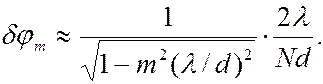(6.37.37)

При пропускании белого света все максимумы, кроме центрального, разложатся в спектр. Начиная со спектров 2-го и 3-го порядков максимумы начинают частично перекрывать друг друга, фиолетовый край максимума (m+1)-го порядка перекрывает красный край максимума m-го порядка.

Дифракционная решётка используется в спектральных приборах в качестве диспергирующей системы для пространственного разложения электромагнитного излучения в спектр. Основными характеристиками дифракционной решетки как спектрального прибора являются дисперсия и разрешающая сила. Угловая дисперсия дифракционной решётки определяется соотношением

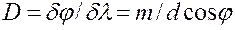; (6.37.38)

линейная дисперсия

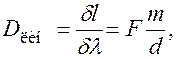(6.37.39)

где 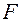– фокусное расстояние линзы, собирающей дифрагирующие лучи на экране.

Разрешающая сила дифракционной решётки

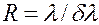(6.37.40)

пропорциональна порядку спектра 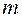и числу щелей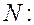

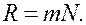(6.37.41)