Дифракция Френеля от круглого отверстия и круглого диска
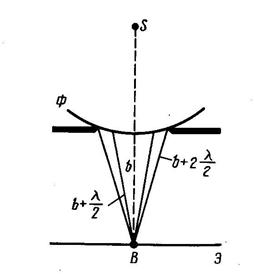 Дифракция от круглого отверстия. Пусть на непрозрачный экран, в котором имеется круглое отверстие радиуса
Дифракция от круглого отверстия. Пусть на непрозрачный экран, в котором имеется круглое отверстие радиуса 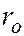 , падает монохроматическая сферическая волна от источника
, падает монохроматическая сферическая волна от источника 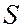 . Если радиус отверстия удовлетворяет условию (6.37.23)
. Если радиус отверстия удовлетворяет условию (6.37.23)
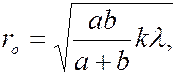
то отверстие оставит открытыми 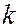 первых зон Френеля, построенных для точки наблюдения
первых зон Френеля, построенных для точки наблюдения 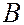 . Вид дифракционной картины в точке
. Вид дифракционной картины в точке 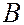 зависит от числа открываемых зон Френеля. Амплитуда результирующих колебаний в точке
зависит от числа открываемых зон Френеля. Амплитуда результирующих колебаний в точке 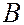 будет равна:
будет равна:
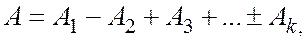
где знак плюс соответствует нечетным 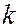 , а минус – четным
, а минус – четным 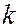 . По аналогии с (6.37.25) это выражение можно привести к виду
. По аналогии с (6.37.25) это выражение можно привести к виду
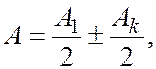 (6.37.26)
(6.37.26)
где знак плюс соответствует нечетным 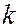 , а минус – четным
, а минус – четным 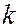 . При малых
. При малых 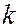 амплитуда
амплитуда 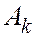 по величине мало отличается от
по величине мало отличается от 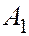 . Следовательно, при нечетных
. Следовательно, при нечетных 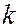 разультирующая амплитуда в точке
разультирующая амплитуда в точке 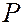 равна
равна 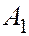 , при четных
, при четных 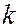 результирующая амплитуда равна нулю. В первом случае в центре дифракционной картины на экране наблюдается светлое пятно, окруженное чередующимися темными и светлыми кольцевыми полосами, во втором – темное.
результирующая амплитуда равна нулю. В первом случае в центре дифракционной картины на экране наблюдается светлое пятно, окруженное чередующимися темными и светлыми кольцевыми полосами, во втором – темное.
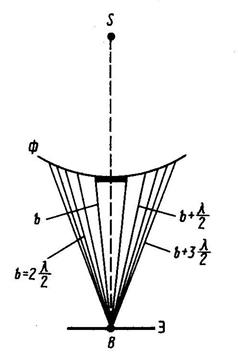 Дифракция от круглого диска. Пусть между источником света
Дифракция от круглого диска. Пусть между источником света 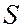 и точкой наблюдения
и точкой наблюдения 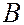 находится непрозрачный диск, радиус которого совпадает с радиусом
находится непрозрачный диск, радиус которого совпадает с радиусом 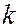 -й зоны Френеля:
-й зоны Френеля: 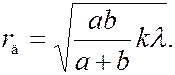 Тогда диск перекрывает первые
Тогда диск перекрывает первые 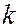 зон Френеля. Амплитуда световой волны в точке
зон Френеля. Амплитуда световой волны в точке 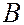 будет равна:
будет равна:
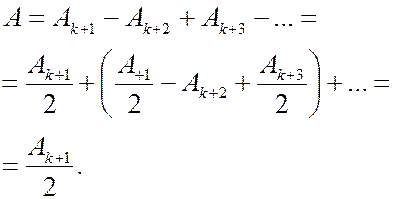
В центре дифракционной картины при любом (четном или нечетном) 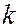 будет наблюдаться светлое пятно. Если число закрытых зон мало, то
будет наблюдаться светлое пятно. Если число закрытых зон мало, то 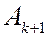 будет мало отличаться от
будет мало отличаться от 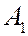 . Поэтому в точке
. Поэтому в точке 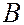 интенсивность будет почти такая же, как при отсутствии диска между
интенсивность будет почти такая же, как при отсутствии диска между 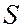 и
и 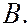
Дата добавления: 2015-05-26; просмотров: 1158;
