Дифракция света

Дифракция света. Принцип Гюйгенса – Френеля. Метод зон Френеля. Доказательство прямолинейности распространения света. Дифракция Френеля на круглом отверстии и диске. Дифракция Фраунгофера на одной щели. Дифракционная решетка. Основные характеристики спектральных приборов: дисперсия и разрешающая способность. Дифракция рентгеновских лучей. Понятие о голографии.

6.3.1. Принцип Гюйгенса – Френеля. Метод зон Френеля

Дифракция света (от лат. diffractus – разломанный, преломлённый) – отклонение при распространении света от законов геометрической оптики, выражающееся в огибании лучами света границы непрозрачных тел, проникновение света в область геометрической тени, огибание светом малых препятствий. Дифракция наблюдается при распространении света в среде с резко выраженными неоднородностями. Дифракция света – проявление волновых свойств света в предельных условиях перехода от волновой оптики к геометрической. Явление дифракции света можно объяснить на основании принципа Гюйгенса.

Принцип Гюйгенса – принцип, согласно которому каждая точка волнового фронта в данный момент времени является центром вторичных элементарных волн, огибающая которых дает положение волнового фронта в следующий момент времени. Принцип Гюйгенса позволяет объяснить законы отражения и преломления света, однако он недостаточен для объяснения дифракционных явлений, Френелем, который дополнил принцип Гюйгенса представлением об интерференции вторичных волн.

Гюйгенса-Френеля принцип – дальнейшее развитие принципа Х.Гюйгенса О.Френелем, введшего представление о когерентности и интерференции вторичных элементарных волн. Согласно принципу Гюйгенса-Френеля волновое возмущение в некоторой точке может быть представлено как результат интерференции когерентных вторичных элементарных волн, излучаемых каждым элементом некоторой волновой поверхности (волнового фронта). Принцип Гюйгенса-Френеля позволяет объяснить и дифракционные явления. Каждый элемент волновой поверхности площадью 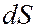является источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента. В точку наблюдения 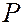от этого элемента приходит колебание

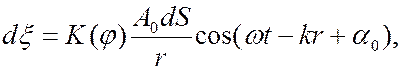(6.37.21)

где 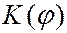– коэффициент, зависящий от угла 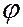между нормалью к поверхности 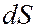и направлением на точку наблюдения; 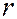– расстояние от элемента поверхности до точки наблюдения; 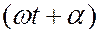– фаза колебания в месте расположения элемента 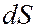. Результирующее колебание в точке наблюдения представляет собой суперпозицию когерентных колебаний от всех элементов волновой поверхности, пришедших в точку наблюдения. Для расчета амплитуды результирующего колебания для случаев, отличающихся симметрией, Френель предложил метод, получивший название метода зон Френеля. Различают два вида дифракции: дифракция Фраунгофера и дифракция Френеля.

Дифракция Фраунгофера(в параллельных лучах) – дифракция плоских волн на препятствии (источник света удалён от препятствия на бесконечно большое расстояние).

Дифракция Френеля– дифракция сферической световой волны на неоднородности (например, отверстии в экране). Дифракция Френеля осуществляется в тех случаях, когда источник света и экран, служащий для наблюдения дифракционной картины, находятся на конечных расстояниях от препятствия, вызвавшего дифракцию.

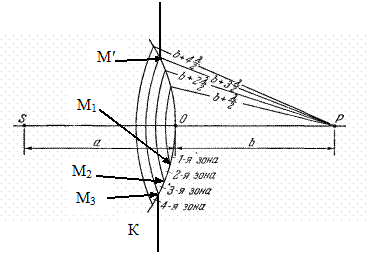Метод зон Френеля.Зоны Френеля– кольцевые участки, на которые разбивают сферическую поверхность фронта световой волны при рассмотрении задач о дифракции волн в соответствии с принципом Гюйгенса – Френеля для упрощения вычислений при определении амплитуды волны в заданной точке пространства. Пусть монохроматическая волна распространяется из точки 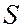в точку наблюдения 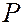. Положение волнового фронта в определенный момент времени указано на рисунке. 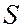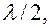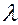Согласно принципу Гюйгенса – Френеля действие источника заменяют действием вторичных (воображаемых) источников, расположенных на поверхности фронта сферической волны, которую разбивают на кольцевые зоны так, чтобы расстояния от краёв соседних зон до точки наблюдения отличались на где – длина волны. (На рисунке 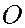– точка пересечения фронта волны с линией 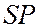, расстояние 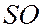= 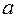, 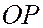= 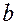). Тогда расстояние 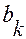от края 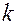-й зоны до точки наблюдения равно

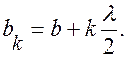(6.37.22)

Внешний радиус 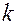-й зоны Френеля

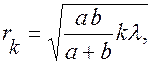(6.37.23)

площадь 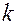-й зоны

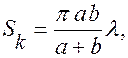(6.37.24)

при не слишком больших 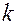площади зон Френеля одинаковы.

Так как колебания от соседних зон проходят до точки 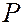расстояния, отличающиеся на 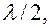то в точку 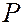они приходят в противофазе. При вычислении амплитуды результирующего колебания в точке 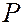методом зон Френеля необходимо также учесть, что с ростом номера зоны амплитуды колебаний, приходящих в точку 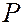, монотонноубывают: А₁> А₂ > А₃ > А₄ > …. Можно положить, что амплитуда колебания А_m равна среднему арифметическому амплитуд примыкающих к ней зон: 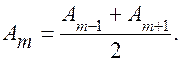Поэтому амплитуда 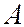результирующего светового колебания, приходящего от всего волнового фронта в точку 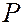будет равна:

А = А₁ – А₂ + А₃ – А₄ + …….. 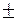А_к .

Это выражение можно представить в следующем виде:

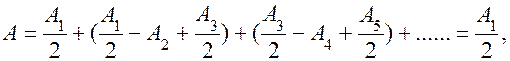(6.37.25)

так как выражения в скобках равны нулю, а амплитуда от последней зоны Френеля бесконечно мала. Следовательно, амплитуда, создаваемая в точке 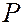всем сферическим волновым фронтом, равна половине амплитуды, создаваемой центральной зоной Френеля. Если 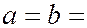1м, 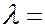0,5 мкм, то радиус первой зоны Френеля равен 0,5 мм. Следовательно, свет от источника к точке наблюдения 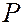распространяется как бы в пределах узкого прямого канала, т.е. практически прямолинейно.

Колебания от четных и нечетных зон Френеля находятся в противофазе и взаимно ослабляют друг друга. Если какое-либо препятствие перекрывает часть сферического волнового фронта, то при расчете амплитуды результирующего колебания в точке наблюдения методом зон Френеля учитываются только открытые зоны Френеля. Если поставить на пути световой волны пластинку, которая перекрывала бы все четные или нечетные зоны Френеля, то амплитуда колебания в точке наблюдения резко возрастает. Такая пластинка называется зонной. Зонная пластинка во много раз увеличивает интенсивность света в точке 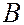, действуя подобно собирающей линзе.