Дифракция Фраунгофера от щели
Пусть на бесконечно длинную щель шириной 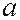 нормально падает плоская монохроматическая световая волна с длиной волны
нормально падает плоская монохроматическая световая волна с длиной волны 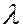 . Поместим за щелью собират
. Поместим за щелью собират  ельную линзу, а в фокальной плоскости линзы экран. Волновая поверхность падающей волны. Плоскость щели и экран параллельны друг другу. Вторичные волны, посылаемые элементами волновой поверхности, совпадающей с плоскостью щели, под углом
ельную линзу, а в фокальной плоскости линзы экран. Волновая поверхность падающей волны. Плоскость щели и экран параллельны друг другу. Вторичные волны, посылаемые элементами волновой поверхности, совпадающей с плоскостью щели, под углом 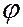 к оптической оси линзы соберутся в точке
к оптической оси линзы соберутся в точке 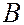 в фокальной плоскости линзы. Оптическая разность хода лучей
в фокальной плоскости линзы. Оптическая разность хода лучей 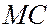 и
и 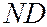 , идущих от краев щели в направлении
, идущих от краев щели в направлении 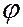 , равна
, равна
 . (6.37.27)
. (6.37.27)
Если разность хода 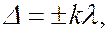 то открытую часть волновой поверхности, совпадающей с плоскостью щели, можно разбить на
то открытую часть волновой поверхности, совпадающей с плоскостью щели, можно разбить на 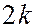 равных по ширине зон, разность хода от краев которых будет равна
равных по ширине зон, разность хода от краев которых будет равна 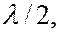 т.е на
т.е на 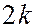 зон Френеля (четное число). Колебания от двух соседних зон будут приходить в точку
зон Френеля (четное число). Колебания от двух соседних зон будут приходить в точку 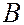 в противофазе и взаимно погашать друг друга. Результирующая амплитуда в точке
в противофазе и взаимно погашать друг друга. Результирующая амплитуда в точке 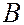 будет равна нулю. Следовательно, если на ширине щели укладывается четное число зон Френеля, то в точке
будет равна нулю. Следовательно, если на ширине щели укладывается четное число зон Френеля, то в точке 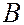 наблюдается дифракционный минимум.
наблюдается дифракционный минимум.
Условие минимума:
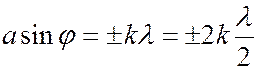 (
( 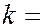 1, 2, 3, ……). (6.37.28)
1, 2, 3, ……). (6.37.28)
Если на ширине щели укладывается нечетное число зон Френеля, то в точке 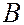 будет наблюдаться дифракционный максимум, т.к. действие одной зоны Френеля будет не скомпенсировано.
будет наблюдаться дифракционный максимум, т.к. действие одной зоны Френеля будет не скомпенсировано.
Условие максимума:
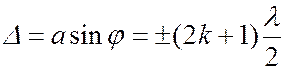 (
( 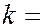 1, 2, 3, ….). (6.37.29)
1, 2, 3, ….). (6.37.29)
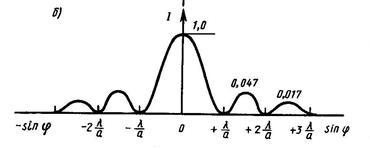 При
При 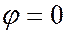 колебания от всех зон будут приходить в точку
колебания от всех зон будут приходить в точку 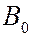 , лежащую против центра линзы, в одной фазе, в этой точке будет наблюдаться центральный максимум с наибольшей интенсивностью.
, лежащую против центра линзы, в одной фазе, в этой точке будет наблюдаться центральный максимум с наибольшей интенсивностью.
Угловая ширина центрального максимума определяется положением минимумов, для которых 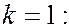
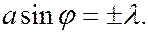 Следовательно, угловая ширина центрального максимума равна:
Следовательно, угловая ширина центрального максимума равна:
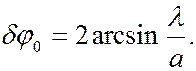 (6.37.30)
(6.37.30)
Если 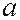 >>
>> 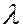 , то:
, то:
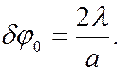 (6.37.31)
(6.37.31)
Дата добавления: 2015-05-26; просмотров: 1310;
