Дифракция Фраунгфера от щели

До сих пор мы рассматривали дифракцию сферических или плоских воли, изучая дифракционную картину в точке наблюдения, лежащей па конечном расстоянии от препятствия. Именно этот круг вопросов был исследован Френелем, и поэтому дифракционные явления такого рода называют обычно дифракцией Френеля.

Фраунгофер (1821—1822 гг.) рассмотрел несколько иной тип явлений. В расположении Фраунгофера труба наводилась на отдаленный источник света (например, на освещенную щель) и наблюдалось изображение его вблизи фокальной плоскости трубы через ее окуляр.

Перед объективом трубы помещался экран с отверстиями, в большей или меньшей степени прикрывающими объектив. Оказалось, что вид изображения наблюдаемого объекта зависит от размеров и формы этих отверстий. Только тогда, когда открыта достаточная часть объектива, изображение имеет вид, точно воспроизводящий форму объекта. При уменьшении же работающей части объектива наблюдаемая картина в большей, или меньшей степени искажается и может даже совсем не напоминать формы источника.

Так, например, при рассматривании удаленной светящейся нити через объектив, прикрытый экраном с узкой щелью, в фокальной плоскости объектива видна светлая, размытая полоса с несколькими максимумами и минимумами.

Таким образом, изображение, даваемое объективом, есть всегда дифракционная картина, возникающая вследствие ограничения сечения светового пучка.

Это ограничение осуществляется так называемой апертурной диафрагмой объектива, роль которой в простейшем случае играет оправа какой-либо линзы объектива или специальная диафрагма. При значительной работающей части объектива (широкая апертурная диафрагма) наблюдаемая дифракционная картина хорошо воспроизводит вид объекта; при малых ее размерах изображение может сильно (до неузнаваемости) отличаться от объекта.

Так как наблюдение по описанному методу ведется в плоскости, сопряженной с плоскостью источника, т. е. в том месте, где свет собирается линзой трубы, то дифракционная картина значительно выигрывает в яркости, и ее наблюдение облегчается. Тип дифракции, при котором рассматривается дифракционная картина, образованная параллельными лучами, получил название дифракции Фраунгофера.

Хотя принципиально фраунгоферова дифракция не отличается от рассмотренной выше дифракции Френеля, тем не менее подробное рассмотрение этого случая весьма существенно. Математический разбор многих важных, примеров дифракции Фраунгофера не труден и позволяет до конца рассмотреть поставленную задачу. Практически же этот случай весьма важен, ибо он находит применение при рассмотрении многих вопросов, касающихся действия оптических приборов (дифракционной решетки, оптических инструментов и т. д.).

Условия, близкие к условиям Фраунгофера, можно осуществить, поместив малый источник света в фокусе линзы и собрав свет при помощи второй линзы в некоторой точке экрана, расположенного в ее фокальной плоскости. Эта точка служит изображением источника. Помещая между линзами экраны с отверстиями различной величины и формы, мы меняем характер дифракционной картины, являющейся изображением источника; в зависимости от размеров и формы отверстий часть света пойдет по тем или иным направлениям и будет собираться в различных точках приемного экрана. В результате изображение будет иметь вид пятна, освещенность которого меняется от места к месту. Решить задачу дифракции — значит найти это распределение освещенности на экране в зависимости от размеров и фермы препятствий, вызывающих дифракцию света. Мы ограничимся разбором наиболее простых и в то же время наиболее важных случаев, когда отверстие имеет форму прямоугольника или круга в непрозрачных экранах.

Наибольшее значение имеет случай; когда прямоугольное отверстие имеет незначительную ширину и бесконечную длину, т. е. является щелью. Практически, конечно, достаточно, чтобы ее длина была значительно больше ширины. Так, при ширине в 0,01—0,02 мм длина щели в несколько миллиметров может считаться бесконечной. В этом случае изображение точки растянется в полоску с максимумами и минимумами и направлении, перпендикулярном к щели, ибо свет дифрагирует вправо и влево от щели. При повороте щели около оси трубы вся картина также повернется. Если в качестве источника взять светящуюся пить, параллельную щели, то различные точки нити будут некогерентными между собой источниками и общая картина будет простым наложением картин от точечных источников. Мы будем наблюдать изображение нити, растянутое в направлении, перпендикулярном к направлению щели, т. е. опять-таки можем ограничиться рассмотрением картины в одном измерении.

Пусть волна падает нормально к плоскости щели. Разобьем площадь щели на ряд узких параллельных полосок равной ширины. Каждая из этих полосок может рассматриваться как источник волн, причем фазы всех этих волн одинаковы, ибо при нормальном падении плоскость щели совпадает с фронтом волны; кроме того, и амплитуды наших элементарных волн будут одинаковы, ибо выбранные элементы имеют равные площади и одинаково наклонены к направлению наблюдения.

Эти два обстоятельства — равенство фаз и равенство амплитуд — чрезвычайно упрощают как графическое, так и аналитическое решение рассматриваемой задачи.

Графически результат сложения амплитуд для любой точки экрана можно представить векторными диаграммами рис. 5.1.

Диаграмма рис. 5.1, а соответствует совпадению направления наблюдения и первоначального направления волны (φ = 0), при котором элементарные волны не приобретают никакой разности фаз. Результирующая амплитуда s = A₀. Диаграмма рис. 5.1, б соответствует направлению, при котором крайние элементы волнового фронта в пределах щели дают разность фаз, равную π, т. е. разность хода, равную λ/2. Из рис. 5.2 видно, что это направление соответствует условию ED = bsin φ – ½ λ , где b – ширина щели FE. Результирующая амплитуда выражается вектором s = 2A₀ /π , ибо s равно диаметру полуокружности, длина которой равна А₀. Диаграмма рис. 5.1,в соответствует разности хода лучей от крайних элементов волнового фронта, равной λ, т. е. соответствует направлению, определяемому условием bsin φ = λ. Результирующая амп­литуда равна нулю, т. е. в указанном направлении света не будет. Нетрудно видеть, что нулевая амплитуда будет соответствовать так же направлению, при котором разность хода от крайних элементов будет равна 2λ; следующий минимум соответствует разности хода 3λ и т.д., т.е. минимумы соответствуют направлениям:

sin φ = λ/b, 2/λb , …, nλ /b,

где п — целое число.

Для аналитического расчета интенсивности света, распространяющегося по разным направлениям за щелью, напишем выражение для волны, посылаемой каждым элементом волнового фронта, и просуммируем действие всех элементов. Амплитуда волны, обусловленной одним таким элементом, пропорциональна его ширине dx, т. е. равна Сdх. Множитель С определится из условия, что по направлению φ = 0 амплитуда волны, посылаемой всей щелью, равна А₀, т. е. Сb= А₀ или С = А₀/b. Таким образом, световое возмущение в соответствующем участке щели выразится соотношением

Для отыскания действия всей щели в направлении, определяемом углом φ с первоначальным направлением, необходимо учесть разность фаз, характеризующую волны, доходящие от различных элементов волнового фронта до пункта наблюдения В _φ , (см. рис. 5.2).

Проведем плоскость FD, перпендикулярную к направлению нормалей дифрагировавших волн. Распределение фаз, которое будет иметь место па этой плоскости, определяет соотношение фаз элементарных волн, собирающихся в точке В _φ , ибо линза не вносит дополнительной разности фаз (таутохронизм). Таким образом, достаточно определить разность хода, возникающую на пути от плоскости FE до плоскости FD. Из рис. 5.2 видно, что разность хода между волнами, идущими от элементарной зоны при точке F (край щели) и от какой-либо точки N (лежащей на расстоянии х от края щели), есть NP = хsinφ. Световое возмущение в точке Р плоскости FD запишется следующим образом:

где k == 2π/λ — волновое число. Результирующее возмущение в точке В _φ определится как сумма этих выражений, т. е. выразится интегралом по всей ширине щели (по всем значениям kот нуля до b). Итак,

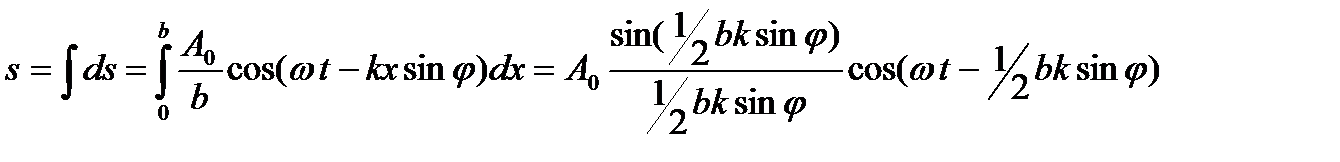
Таким образом, результирующая волна, идущая в направлении φ имеет амплитуду

(5.1)

так как k = 2π/λ . Во многих практических случаях, в частности при наблюдении в трубу, угол φ настолько мал, что можно положить sin φ=φ, и тогда получим

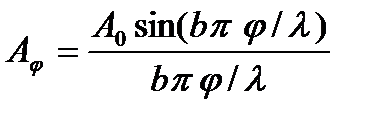(5.2)

Выражение (5.2) показывает, что вдоль экрана (с изменением φ) освещенность меняется, проходя через максимумы и минимумы.

Исследуем выражение (5.1). А_φ обращается в нуль для углов φ, удовлетворяющих условию (bπ/ λ)sin φ =п π , где п = 1, 2, 3, ... (целые числа), т. е. для

sin φ =п λ /b (5.3)

Условие (5.3) определяет направления на точки экрана (и соответственно их положения), в которых амплитуда равна нулю и, следовательно, интенсивность минимальна. Оно совпадает с условием, выведенным выше графическим путем.

При определенных промежуточных значениях угла φ амплитуда достигает максимальных и минимальных значений. Наибольший максимум имеет место, когда

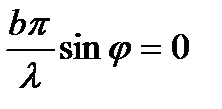
т.е. φ=0; при этом А_φ =А₀.

Следующие максимумы, значительно уступающие по абсолютной величине главному, соответствуют значениям φ, определенным из условий:

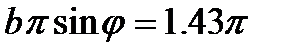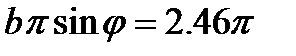, , , и т.д.

На рис. 5.3 показана кривая распределения интенсивности (сплошная кривая)

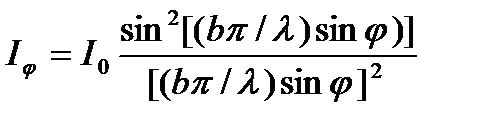
где I₀ = A₀² есть интенсивность света, идущего от щели шириной b в направлении первичного пучка.

Как видно из рис. 5.3, величина вторичных максимумов быстро убывает.