Спряжені (двоїсті) задачі лінійного програмування. Основні властивості
Розглянемо основну ЗЛП, записану (без зменшення загальності міркувань) у вигляді:
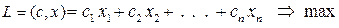 (8.1)
(8.1)
при обмеженнях
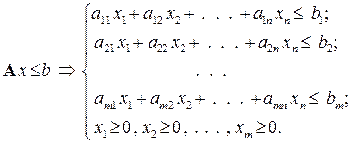 (8.2)
(8.2)
Розглянемо, також, задачу:
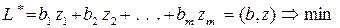 (8.3)
(8.3)
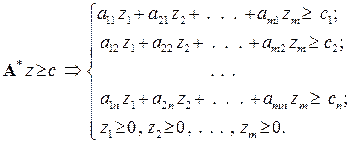 (8.4)
(8.4)
Задачу (8.3), (8.4) одержана із задачі (8.1), (8.2) згідно з такими правилами:
1) вільні члени обмежень (8.2) 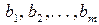 є коефіцієнтами нового критерію
є коефіцієнтами нового критерію 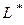 , а коефіцієнти
, а коефіцієнти 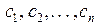 в критерії
в критерії 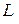 – вільними членами в обмеженнях (8.4);
– вільними членами в обмеженнях (8.4);
2) матрицею коефіцієнтів нових обмежень є матриця 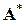 , що одержана транспонуванням матриці
, що одержана транспонуванням матриці 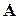 ;
;
3) у нових обмеженнях (8.4) знаки нерівностей протилежні знакам нерівностей (8.2);
4) максимізація критерію 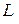 змінюється на мінімізацію критерія
змінюється на мінімізацію критерія 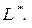
Задача (8.3), (8.4) називається спряженою (двоїстою) до задачі
(8.1), (8.2).
Не важко помітити, що задачу (8.1), (8.2) можна розглядати як спряжену відносно своєї спряженої задачі (8.3), (8.4) або 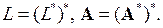
Властивість 1. Якщо одна зі спряжених задач (8.1), (8.2) чи (8.3), (8.4) має розв’язок, то й інша має розв’язок, причому виконується рівність:
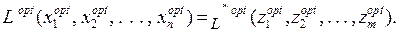
Якщо ж в одній із цих задач лінійна форма необмежена, то спряжена задача має порожню область обмежень.
Властивість 2. Якщо хоча б один розв’язок однієї із взаємоспряжених задач перетворює і-те обмеження цієї задачі в строгу нерівність, то кожна і-та компонента кожного оптимального розв’язку іншої спряженої задачі дорівнює нулю.
Якщо ж і-та компонента оптимального розв’язку однієї зі спряжених задач строго додатна, то кожний оптимальний розв’язок іншої спряженої задачі перетворює і-те обмеження цієї задачі на рівність.
Інакше кажучи, оптимальні розв’язки 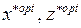 пари спряжених задач задовольняють умови:
пари спряжених задач задовольняють умови:
1) 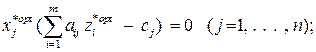
2) 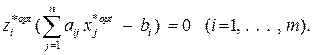
Приклад. Сформулювати ЗЛП, спряжену до заданої:
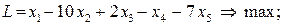
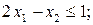
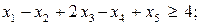
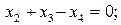
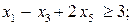
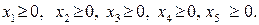
Розв’язування Запишемо нерівності у формі (8.2):
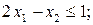
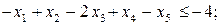
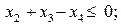
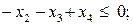
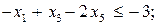
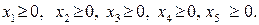
Задача лінійного програмування, спряжена до заданої, має такий вигляд:
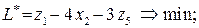
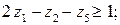
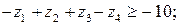
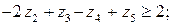
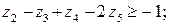
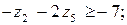
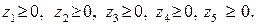
Розв’язують спряжені задачі, так само, як і прямі за допомогою симплекс-методу.
Завдання для самостійних і контрольних робіт
Розв’язати ЗЛП: спряжену до заданї.
1. 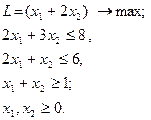
| 2. 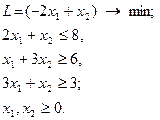
|
3. 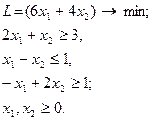
| 4. 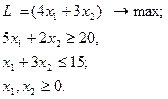
|
5. 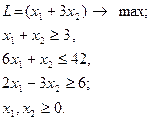
| 6. 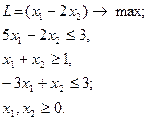
|
7.  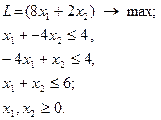
| 8. 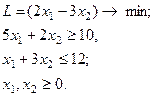
|
9. 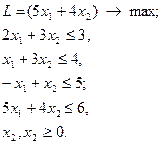
| 10. 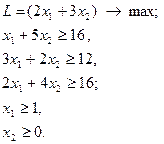
|
11. 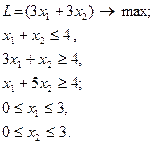
| 12. 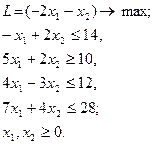
|
13. 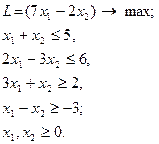
| 14. 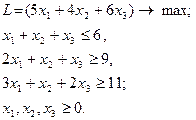
|
15. 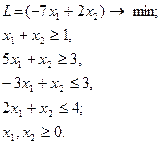
| 16. 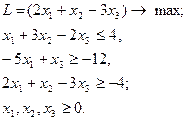
|
17. 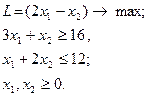
| 18. 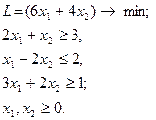
|
19. 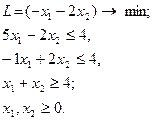
| 20. 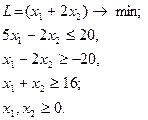
|
21. 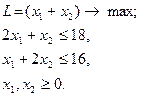
| 22. 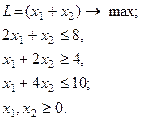
|
23. 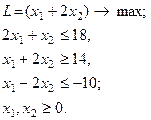
| 24. 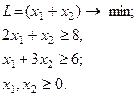
|
25. 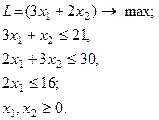
| 26. 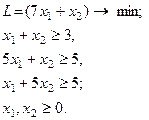
|
27. 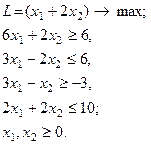
| 28. 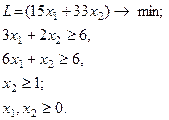
|
29. 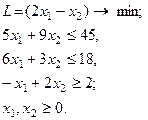
| 31. 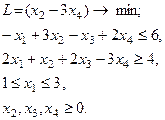
|
30. 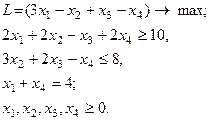
| 32. 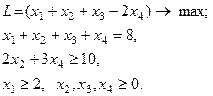
|
Дата добавления: 2015-06-12; просмотров: 2464;
