Взаимодействие рентгеновского излучения

Взаимодействие рентгеновского излучения с веществом в основ­ном аналогично взаимодействию 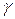-излучения, поскольку, также пред­ставляет собой электромагнитное излучение. Энергия его фотонов лежит, как правило, в области от единиц до нескольких сотен килоэлектроновольт, и взаимодействие рентгеновского излучения этого диапазона энергий описывается теми же законами, что и 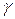-излучение того же диапазона энергий.

Наряду со способностью рентгеновского излучения возбуждать в веществе вторичное рентгеновское излучение в виде рентгеновской флуоресценции, с его помощью можно также возбуждать в облучае­мом веществе люминесценцию, представляющую собой избыточ­ное над тепловым неравновесное излучение в ультрафиолетовом (УФ) видимом и инфракрасном (ИК) спектральных диапазонах. Это явле­ние получило название рентгенолюминесценции (РЛ).

Рентгеновское излучение может возбуждать люминесценцию как в основном веществе минерала, так и находящихся в нем различных примесях, называемых центрами люминесценции [25].

Итак, люминесценция - это излучение, возникшее под каким-либо внешним воздействием. Следовательно, ее можно оценивать набо­ром определенных, спектроскопических (спектры поглощения, воз­буждения и излучения) и кинетических (изменение свечения во вре­мени) характеристик.

Важнейшими спектральными характеристиками люминесценции являются спектры возбуждения, поглощения и излучения.

Спектр поглощенияминерала представляет собой зависимость коэффициента поглощения 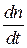от частоты 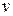(длины волны 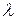) облучае­мого минерала излучения или его энергии Е. В соответствии с зако­ном Бугера-Ламберта интенсивность излучения I, прошедшего че­рез слой минерала толщиной d, определяется уравнением

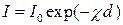, (1.2.2.1)

где I₀ - интенсивность падающего излучения. Отсюда

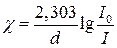, (1.2.2.2)

Величина D = 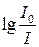носит название оптической плотности. По вели­чине 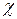можно судить, происходит ли поглощение в основном веще­стве минерала или примесями-активаторами. Спектр поглощения позволяет определить ширину Е_g запрещенной зоны.

Спектр возбужденияпредставляет собой зависимость интен­сивности люминесценции от длины волны 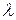(частоты 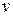) или энергии Е возбуждающего излучения при одной и той же его интенсивности. Спектр возбуждения существенно отличается от спектра поглоще­ния, т.к. доля поглощаемого излучения, преобразуемая в свет люми­несценции, различна в различных участках спектра. Интенсивность полосы активаторного поглощения обычно значительно меньше ин­тенсивности фундаментальной полосы вследствие малой концентра­ции активаторных центров. В то же время люминесценция в этой полосе возбуждается весьма эффективно, что используется для вы­явления активаторных полос поглощения. В тех случаях, когда лю­минесценция представляет собой исключительно внутри центровой процесс, излучение, поглощаемое основной решеткой минерала, мо­жет оказаться неактивным. Люминесценция таких минералов, как правило, плохо возбуждается рентгеновским излучением. Изучение спектров возбуждения минералов позволяет определить энергию (дли­ну волны или частоту) облучающего излучения, при которой можно более эффективно возбуждать люминесценцию минералов.

Спектр излученияпредставляет собой распределение интен­сивности люминесценции по длинам волн 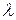(частотам 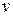) или по энер­гии квантов Е и состоит обычно из одной или нескольких полос. Изу­чение спектров излучения позволяет определить, в каком спектраль­ном диапазоне энергий (длин волн или частот) необходимо регистри­ровать люминесценцию минералов, чтобы наилучшим образом вы­делять свечение минералов с полезными компонентами. Спектры люминесценции ряда минералов приведены на рис. 1.2.2.1. Приведен­ные зависимости иллюстрируют различие минералов не только по интенсивности свечения, но и по его цвету, определяемому длиной волны. Кристаллический характер структуры минералов дает воз­можность использовать для описания их люминесценции представ­ления физики твердого тела и, в частности, зонной теории твердых тел. К зонной схеме обычно приходят, рассматривая изменения в энергетической диаграмме атомов при их сближении. В этом случае энергетические уровни валентных электронов расщепляются на боль­шое число уровней, расположенных столь близко друг к другу, что фактически они сливаются в одну зону, называемую валентной.

Соответственно, более высоко расположенные уровни образуют зону проводимости. В случае полупроводников и диэлектриков ва­лентная зона и зона проводимости разделены промежутком - поло­сой запрещенных состояний, или запрещенной зоной. Поскольку при­месные атомы активатора внедрены в кристаллическую решетку минерала, и находятся далеко друг от друга, то резонансного рас­щепления уровней и слияния их в зону не происходит. Следовательно, они остаются локальными. Здесь мы имеем дело с энергетической диаграммой всего кристалла, а не отдельных составляющих его ча­стиц. Примерное соотношение элементарных актов, происходящих при люминесценции минералов, и их последовательность приведены на рис. 1.2.2.2.

Локальные уровни изображены короткими черточками, а зоны -заштрихованными прямоугольниками. Цифрой 1 обозначена зона про­водимости (1^/ -уровни вблизи дна, 1^//-где-нибудь в середине). Циф­рой 2 обозначен возбужденный уровень центра люминесценции. 3 и 3^/ - уровни электронных ловушек (они бывают разной величины); 4 -основной уровень центра люминесценции; 5 и 5^/ -уровни дырочных ловушек (они тоже бывают разной величины). Цифрой 6 обозначена валентная зона (6^/-уровни вблизи ее дна, 6^//- где-нибудь в середи­не). Стрелки на рис. 1.2.2.2 обозначают переходы электронов. Дырки совершают переходы в обратном направлении.

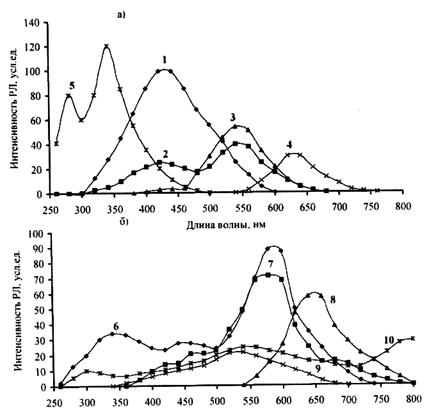
Рис. 1.2.2.1. Спектры РЛ минералов:

а - шеелит (1), молибдошеелит (2), повеллит (3), кальцит (4). флюорит (5); б - апатит (6), циркон (7), волластонит (8), плагиоклаз (9), актинолит(10)

Волнистые наклон­ные стрелки обозначают потерю энергии свободными электронами и дырками при взаимодействии с колебаниями кристаллической решет­ки минерала.

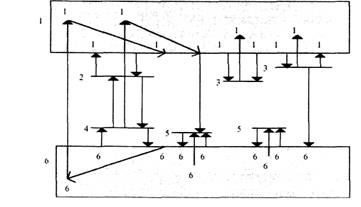
Рис. 1.2.2.2. Зонная модель минерала

Как на рис. 1.2.2.2, так и на схеме рис. 1.2.2.3 указаны только главные процессы, происходящие при возбуждении и развитии люминесцен­ции. В частности, предполагается, что кванты света (люминесцен­ции) испускаются только после рекомбинации (воссоединении) сво­бодных электронов с дырками и притом только с теми, которые рас­положены на ловушках одного сорта. Эти ловушки называются цен­трами люминесценции (иногда - центрами активатора, т.к. они обра­зуются примесями-активаторами, присутствующими в кристалличес­кой решетке минерала). Центрами люминесценции могут служить не только примеси, но и собственные дефекты решетки, например вакансии или междоузельные атомы тех же элементов, из которых состоит кристаллическая решетка минерала.

При облучении минерала рентгеновским излучением возбужде­ние минерала начинается с поглощения рентгеновских фотонов (см. схемы на рис. 1.2.2.2, 1.2.2.3). Оно может происходить либо в центрах лю­минесценции (активатора) (переходы 4 —> 2 и 4 —> 1^//), либо в основ­ной веществе (переходы 6^// —> 1^//). При поглощении излучения в ос­новном веществе происходит образование свободных электронов и дырок, обладающих энергией, значительно превышающей тепловую. Мигрируя по кристаллу, они постепенно растрачивают энергию - до тех пор, пока не дойдут до края соответствующей зоны (переходы 1^// —>1^/ для электронов и 6^//> 6^/ для дырок).

Рис. 1.2.2.3. Схема процессов в минерале во время люминесценции

Аналогичный процесс потери энергии происходит и после погло­щения излучения центром люминесценции. Он отличается, однако, от предыдущего: во-первых, возможно промежуточное возбужденное состояние центра люминесценции 2, из которого происходит как ионизация (2 →1), так и возвращение в основное состояние с излучением (2 → 4) - флуоресценция (флуоресценцией называется процесс люминесценции, длительность которого не более 10^-8 с); во вторых, дырки получаются не свободными, а остаются на центрах люминесценции 4, т.е. центры люминесценции остаются в ионизован­ном состоянии. При возбуждении в основном веществе дырки в кон­це концов тоже попадают на центры люминесценции (4 → 6), т.е. центры люминесценции в итоге тоже оказываются ионизованными, но до этого дырки могут несколько раз побывать в более мелких ловушках и освободиться из них (5 ↔ 6). Электроны, вырванные из­лучением из центров люминесценции, могут рекомбинировать с иони­зованными центрами или попасть на электронные ловушки (1 →3 и 1 →3^/ ).

Конечной стадией возбуждения при поглощении возбуждающего излучения как центрами люминесценции, так и основным веществом минерала является состояние, когда центры люминесценции (центры активатора) ионизованы, а оторванные от них электроны захвачены ловушками. Такое состояние называется возбужденным.

Освобождение электронов из ловушек (3 →1 и 3^/→1) может про­исходить как благодаря тепловым колебаниям, так и при поглощении падающего на минерал излучения, возбуждающего люминесценцию, или под действием длинноволнового, высвечивающего, излучения. Свободные электроны могут опять локализоваться на ловушках либо рекомбинировать с ионизованными центрами (1 → 2). Переход цен­тра люминесценции в основное состояние (2 → 4) сопровождается излучением в виде светового потока люминесценции. Такая люми­несценция называется внутрицентровой.При рекомбинации сво­бодного электрона с ионизированным центром свечения (переход 1 → 5) происходит испускание фотона, т.е. возникает люминесценция, которая называется рекомбинационной.Глубина ловушек в значи­тельной степени определяет длительность затухания люминесценции минерала, а концентрация ловушек - величину запасенной светосуммы, т.е. энергии, накопленной в минерале при его возбуждении. Рассмотренная зонная модель, при построении которой не учиты­ваются колебательные движения атомов (ионов), позволяет интер­претировать процессы связанные с миграцией электронов и дырок на расстоянии порядка нескольких постоянных решетки и более. При изучении же внутрицентровой люминесценции колебаниями ре­шетки минерала пренебречь нельзя. В этом случае используют при­ближение, которое носит название модели потенциальных кривых. На рис. 1.2.2.4 приведен общий вид диаграммы потенциальных кривых, на которой нижняя кривая соответствует основному состоянию, а вер­хняя - возбужденному. Стрелка, направленная вверх, отвечает по­глощению кванта возбуждающего излучения, а стрелка, направлен­ная вниз, - возвращению системы в основное состояние, сопровож­даемое испусканием фотона.

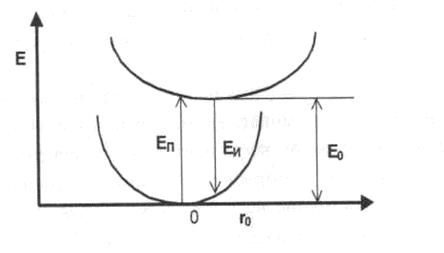
Рис. 1.2.2.4. Модель потенциальных кривых

Поскольку люминесценция возникает при переходе из неравновес­ного состояния в равновесное, то характер ее во многом определяет­ся относительной скоростью различных стадий процесса или, иными словами, закономерностями протекания его во времени, т.е. кинети­кой. Вследствие конечной и притом значительной по сравнению с периодом световых колебаний длительности пребывания системы в возбужденном состоянии люминесценция возникает не сразу после начала возбуждения и не исчезает мгновенно после его прекраще­ния, а разгорается и затухает с определенной скоростью.

Изучение процессов разгорания и затухания люминесценции служит одним из важных источников информации о механизме испуска­ния света минералами. Воспользуемся простейшей зонной схемой минерала, изображенной на рис. 1.2.2.5. Будем считать, что каждый акт поглощения минералом возбуждающего излучения центром люми­несценции приводит к его ионизации и тем самым к появлению элек­трона в зоне проводимости, а каждый акт рекомбинации - к излуче­нию, т.е. вопросы внутреннего тушения люминесценции рассматри­вать не будем. Наше допущение означает следующее: если совер­шается переход 4→ 2 , то обязательно произойдет и переход 2→ 1^/, и наоборот, если совершился переход 1^/→2, обязательно про­изойдет и переход 2→ 4 и притом с испусканием кванта света. При этом мы не учитываем возбужденного состояния центра люминес­ценции, т.к. для простоты считаем, что время задержки электрона в этом состоянии мало. Поэтому в нашей схеме будем учитывать только четыре процесса, указанные на рис. 1.2.2.5 стрелками.

Баланс электронов и дырок на центрах люминесценции и на ло­вушках описывается дифференциальными уравнениями, называемыми кинетическими. Решив эти уравнения, можно определить зависимость концентраций свободных и локализованных электронов и дырок от времени. Зная эти концентрации, можно узнать все люми­несцентные свойства минерала.

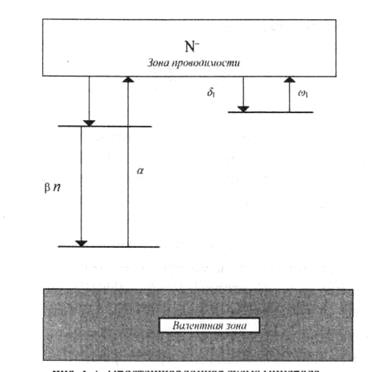
Рис. 1.2.2.5. Простейшая зонная схема минерала

При воздействии на минерал возбуждающим излучением проис­ходит ионизация центров люминесценции n с вероятностью 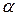, т.е. отрыв от них электронов и переход их в зону проводимости и после их миграции в течение некоторого времени эти свободные электро­ны рекомбинируют с ионизованными центрами люминесценции. Ве­роятность такой рекомбинации пропорциональна концентрации иони­зованных центров п и концентрации свободных электронов в зоне про­водимости N ^-. Поэтому в единицу времени будет исчезать 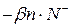центров люминесценции. Величина 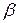называется коэффициентом ре­комбинации свободных электронов с ионизованными центрами лю­минесценции. Скорость изменения концентрации ионизованных цент­ров люминесценции 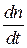определяется разностью их возникновения и исчезновения. Следовательно,

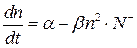(1.2.2.1)

но в процессе возбуждения люминесценции свободные электроны, находящиеся в зоне проводимости, могут быть с вероятностью 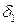_; захвачены ловушками. Концентрацию свободных электронов, захва­ченных ловушками, обозначим за п₁. Число актов локализации элек­тронов будет пропорционально N ^-.

Освобождение электронов из ловушек зависит от нескольких фак­торов, например, температуры минерала, высвечивающего действия возбуждающего или дополнительного излучения, которым облучают минерал в процессе люминесценции. Обозначим вероятность осво­бождения электрона из ловушки через 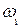. Тогда количество осво­бождаемых в единицу времени электронов равно 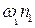и баланс лока­лизованных электронов выразится следующим образом:

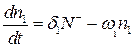. (1.2.2.2)

Таким образом, мы получили систему из двух уравнений (1.2.2.2) и (1.2.2.3) с тремя неизвестными, разрешить которую невозможно. По­этому необходимо добавить еще уравнение нейтральности, отража­ющее тот факт, что все электроны, оторванные от центров люминес­ценции п, расположены либо на ловушка п₁ либо в зоне проводимос­ти N^-:

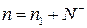. (1.2.2.3)

Чтобы из этих уравнений получить зависимость изменения ин­тенсивности люминесценции минерала от времени, необходимо вы­разить п через t. В общем виде сделать это очень сложно, поэтому рассмотрим случай, когда вероятность рекомбинации электрона с ионизованным центром преобладает над вероятностью его локали­зации в ловушке 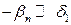. Такой случай может осуществляться при большой интенсивности возбуждения, например, при лазерном или рентгеновском облучении минерала.

Итак, в момент включения возбуждающего люминесценцию ми­нерала излучения начинается процесс ее разгорания. Следователь­но, нарастание интенсивности люминесценции должно происходить за время сопоставимое с временем жизни электрона в зоне проводи­мости, или с временем жизни возбужденного состояния центра лю­минесценции, в зависимости от того, какое время больше.

Математически это может быть показано следующим образом: например, для случая, когда 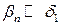, имеем n₁=0, т.е. свободные электроны не захватываются ловушками, следовательно, исходя из условия нейтральности (1.2.2.3) получаем n=N^-. Тогда скорость изме­нения концентрации ионизованных центров люминесценции 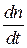- определяется как

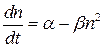. (1.2.2.4)

Решение этого уравнения будет иметь вид

,

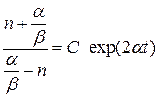а с учетом того, что при t = 0 концентрация ионизованных центров люминесценции п = 0, определяем, что произвольная постоянная С = 1. Следовательно, уравнение для определения п будет иметь вид

.

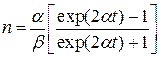Интенсивность свечения I пропорциональна скорости рекомбина­ции электронов с ионизованным центром, а скорость, в свою оче­редь, определяется числом эффективных встреч между ними, т.е. таких встреч, которые приводят к рекомбинации. Можно считать, что это число пропорционально произведению концентраций участ­ников процесса - ионизованных центров N исвободных электронов n (так называются электроны, попавшие в зону проводимости). Сле­довательно, с учетом того, что N = п, окончательно получаем урав­нение изменения интенсивности при разгорании люминесценции ми­нерала

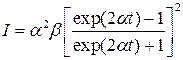. (1.2.2.5)

Рассмотрим процесс затухания люминесценции. Затухание лю­минесценции может быть обусловлено как внутрецентровыми, так и зонными переходами. В первом случае излучательный переход в каждом центре происходит независимо от состояния других цент­ров и определяется только его вероятностью. Поэтому доля возбуж­денных центров свечения, переходящих в основное состояние в еди­ницу времени, остается в течение всего процесса постоянной. Мате­матически это можно записать так:

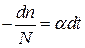, (1.2.2.6)

где N- число возбужденных центров свечения в момент времени t, a - константа скорости процесса. Знак «минус» ставится потому, что с увеличением времени число возбужденных центров уменьшается. Интегрирование этого выражения дает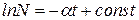

Если в начале затухания (при t=0) число возбужденных центров равно N₀, тo

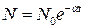. (1.2.2.7)

Интенсивность свечения I определяется числом излучательных переходов в единицу времени

,

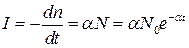Или

,

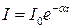где

.

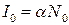Таким образом, приходим к экспоненциальному закону затухания.

Чем больше а, тем быстрее снижается интенсивность люми­несценции и тем меньше средняя продолжительность пребывания центра в возбужденном состоянии 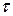. Определяя 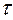известным из ма­тематики выражением

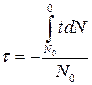, (1.2.2.8)

и подставляя в него значение dN, по­лучим

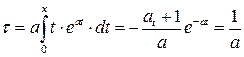.(1.2.2.9)

Таким образом, 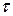равно величине, обратной константе скорости затухания.

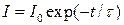. (1.2.2.10)

Откуда видно, что 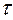- это время, в течение которого интенсив­ность люминесценции уменьшается в е раз.

Теперь рассмотрим кинетику затухания рекомбинационной люми­несценции. Интенсивность свечения /пропорциональна скорости ре­комбинации электронов с ионизованным центром, а скорость, в свою очередь, определяется числом эффективных встреч между ними, т.е. таких встреч, которые приводят к рекомбинации. Можно считать, что это число пропорционально произведению концентраций участ­ников процесса - ионизованных центров N и свободных электронов п (так называются электроны, попавшие в зону проводимости). Сле­довательно

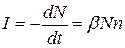, (1.2.2.11)

где β- коэффициент рекомбинации.

Допустим, что минерал имеет один тип центров свечения и не содержит каких-либо других дефектов, которые могут захватывать электрон из зоны проводимости. В таком случае N=n и

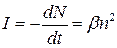. (1.2.2.12)

Разделяя переменные и интегрируя, найдем

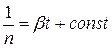. (1.2.2.13)

Если в начальный момент затухания п = п₀ , то в момент времени t

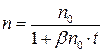, (1.2.2.14)

Подставляя это значение п в уравнение (1.2.2.12), получим

При t = О

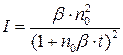, (1.2.2.15)

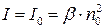, (1.2.2.16)

откуда

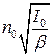. (1.2.2.17)

Таким образом, закон затухания рекомбинационной люминесцен­ции выражается уравнением гиперболы второго порядка. Это урав­нение для его экспериментальной проверки целесообразно преобра­зовать, придав ему следующий вид:

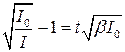
Следовательно, в координатах 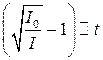должнаполучиться прямая линия. Решить вопрос о том, какой из двух механизмов люминесценции имеет место при конкретных исследованиях, можно с помощью по­лученных уравнений. Если после прекращения возбуждения прошло достаточно много времени, так, что в уравнении (1.2.2.17) можно положить 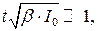то получаем

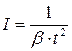, (1.2.2.18)

откуда

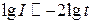, (1.2.2.19)

тогда как при экспоненциальном затухании

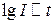. (1.2.2.20)

Таким образом, строя график зависимости 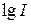от t или от lg t, можно определить, какому из двух механизмов подчиняется процесс затухания люминесценции.