Заселение подоболочек и атомные термы
Особая проблема оболочечной модели заключается в определении порядка заселения подоболочек, когда значения квантовых чисел n и l сохраняются постоянными, и, следовательно, правила Клечковского не действуют. Рассмотрим, например, атом азота с электронной формулой 1s22s22p3. С заполненными подоболочками 1s и 2sпроблем не возникает, тогда как для незаполненной 2p-подоболочки возможно 20 различных способов заселения и, следовательно, должно существовать 20 разновидностей атома азота с указанной электронной формулой.
Поскольку орбитальные энергии всех шести 2р-АСО одинаковы, полная энергия атома оказывается зависящей от величины небольших вкладов, связанных с силами межэлектронного отталкивания и еще более слабыми магнитными силами (спин-орбитальное взаимодействие). Для оценки величины этих вкладов требуется установить значения характеристик глобальных векторов орбитального и спинового моментов:
| L | 2 = h2 × L(L + 1) и LZ = h × ML
| S | 2 = h2 × S(S + 1) и SZ = h × MS
Достаточно очевидно, что глобальные векторы орбитального и спинового моментов должны складываться из соответствующих одноэлектронных векторов. Правила такого сложения зависят от типа атома. Известны две основные схемы:
LS- приближение, справедливое для легких атомов (Z < 20),
jj-приближение, справедливое для тяжелых атомов (Z > 20),
В случае LS-приближения сложение производится отдельно для орбитальных и отдельно для спиновых моментов:
L = l1 + l2 + . . . + ln S = s1 + s2 + . . . + sn
Затем глобальные моменты складываются и образуют вектор полного механического момента атома: J = L + S. Ясно, что при таком подходе спин-орбитальное взаимодействие считается достаточно большим только на уровне глобальных моментов.
В случае jj-приближения сначала складываются локальные орбитальный и спиновой моменты для каждого электрона, образуя одноэлектронные векторы полного механического момента, и только затем отдельные локальные полные моменты складываются в глобальный момент атома:
1) li + si = ji и 2) J = j1 +j2 + … +jn
При использовании такой процедуры спин-орбитальное взаимодействие учитывается уже на уровне отдельных электронов.
Воспользуемся LS-приближением для анализа ситуации с атомом азота. Сложение трех локальных векторов можно выполнить путем сложения их проекций. Длина глобальной проекции определяется суммой магнитных чисел локальных векторов:
ML=ml1+ml2+ml3 MS=ms1+ms2+ms3
Зная длины проекций векторовL и S, можно легко установить и длины самих этих векторов, поскольку выполняется известное правило:
ML= L, (L – 1), ... , (1 – L), –LиMS = S, (S – 1), ... , (1 – S), –S
Для систематического анализа построим специальную таблицу, в которую будем помещать возможные конфигурации с определенными значениями квантовых чисел ML и MS.
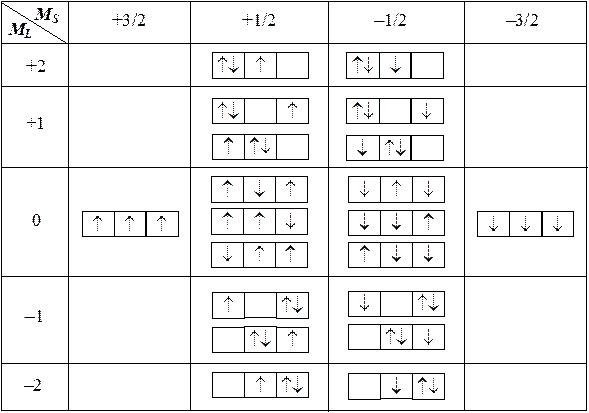
Теперь следует обратить внимание на то, что два момента с определенной длиной, которые определяются квантовыми числами L и S, порождают набор из (2L + 1)(2S + 1) состояний, отличающихся проекциями этих векторов. Этот набор удобно выразить в виде аналогичной таблицы. Очевидно, что эта таблица будет прямоугольной, имеющей (2S + 1) столбцов и (2L + 1) строк. Каждая клетка такой таблицы будет соответствовать только одному состоянию. С учетом этого обстоятельства становится ясно, что полученная выше таблица для атома азота имеет неидеальный вид (в ней имеются пустые клетки и клетки, содержащие несколько конфигураций) и в действительности представляет собой наложение трех идеальных таблиц.
| ML \ MS | +1/2 | –1/2 |
| +2 | ||
| +1 | ||
| –1 | ||
| –2 |
| ML \ MS | +3/2 | +1/2 | –1/2 | –3/2 |
| ML \ MS | +1/2 | –1/2 |
| +1 | ||
| –1 |
Отсюда следует, что совокупность из 20 состояний атома азота распадается на три группы, включающих 4, 6 и 10 состояний, причем в каждой группе выполняется условие: L = const и S = const. Такие группы состояний называются атомными термами. По числу строк и столбцов каждой из трех идеальных таблиц легко определить квантовые числа L и S, которыми определяются длины векторов орбитального и спинового моментов атома.
1) L = 0 S = 3/2 , что соответствует терму 4S (4 состояния)
2) L = 1 S = 1/2 , что соответствует терму 2P (6 состояний)
3) L = 2 S= 1/2 , что соответствует терму 2D (10 состояний)
Все состояния, принадлежащие одному терму, характеризуются одними и теми же значениями орбитального и спинового квантовых чисел L и S, и, следовательно, им соответствует одна и та же пространственная форма электронного облака. В результате и энергия межэлектронного отталкивания будет одинакова для всех таких состояний. Напротив, состояния, принадлежащие различным термам, соответствуют электронным облакам разной пространственной формы, что приводит к различиям в энергиях межэлектронного отталкивания.
Таким образом, зная принадлежность состояний к определенным термам, можно предсказать их распределение по энергетической шкале. Для этого имеются специальные правила Хунда:
1 правило: минимальной энергией обладает терм с максимальной мультиплетностью (значением квантового числа S).
2 правило: при равных мультиплетностях минимальной энергией обладает терм с максимальным квантовым числом L.
Так, для атома азота минимальной энергией будут обладать четыре состояния терма 4S, а максимальной — шесть состояний терма 2P.
Дата добавления: 2015-06-10; просмотров: 1563;
